Integral Formulas – Integration can be considered the reverse process of differentiation or called Inverse Differentiation. Integration is the process of finding a function with its derivative. Basic integration formulas on different functions are mentioned here. Apart from the basic integration formulas, classification of integral formulas and a few sample questions are also given here, which you can practice based on the integration formulas mentioned in this article. When we speak about integration by parts, it is about integrating the product of two functions, say y = uv. More integral calculus concepts are given, so keep learning integral formulas to solve problems accurately. Also, watch the video given below to clear your concept.
| Table of Contents: |
List of Integral Formulas
The list of basic integral formulas is given below:
- ∫ 1 dx = x + C
- ∫ a dx = ax+ C
- ∫ xn dx = ((xn+1)/(n+1))+C ; n≠1
- ∫ sin x dx = – cos x + C
- ∫ cos x dx = sin x + C
- ∫ sec2x dx = tan x + C
- ∫ csc2x dx = -cot x + C
- ∫ sec x (tan x) dx = sec x + C
- ∫ csc x ( cot x) dx = – csc x + C
- ∫ (1/x) dx = ln |x| + C
- ∫ ex dx = ex+ C
- ∫ ax dx = (ax/ln a) + C ; a>0, a≠1
These integral formulas are equally important as differentiation formulas. Some other important integration formulas are:
Basic Integral Formulas PDF
Click here to download the PDF of important basic integral formulas.
Download Integral Formulas PDF
| Also, check: |
Classification of Integral Formulas
The integral formulas can be classified based on following functions.
- Rational functions
- Irrational functions
- Trigonometric functions
- Inverse trigonometric functions
- Hyperbolic functions
- Inverse hyperbolic functions
- Exponential functions
- Logarithmic functions
- Gaussian functions
Integral Formulas for Different Functions
Let’s learn all the integration formulas for different functions now.
Rational functions
Below are the integration formulas for rational functions.
- ∫ 1 dx = x + C
- ∫ a dx = ax+ C
- ∫ (1/x) dx = ln |x| + C
Irrational functions
Let’s see the integration formulas for irrational functions.
- \(\begin{array}{l}\int \frac{1}{\sqrt{1-x^2}} dx = sin^{-1}x + C\end{array} \)
- \(\begin{array}{l}\int \frac{1}{1+x^2} dx = tan^{-1}x + C\end{array} \)
- \(\begin{array}{l}\int \frac{1}{|x|\sqrt{1-x^2}} dx = sec^{-1}x + C\end{array} \)
Trigonometric functions
Integration formulas for trigonometric functions are listed below:
- ∫ sin x dx = – cos x + C
- ∫ cos x dx = sin x + C
- ∫ sec2x dx = tan x + C
- ∫ csc2x dx = -cot x + C
- ∫ sec x (tan x) dx = sec x + C
- ∫ csc x ( cot x) dx = – csc x + C
Inverse trigonometric functions
Go through the integration formulas for inverse trigonometric functions here.
- \(\begin{array}{l}\int sin^{-1}xdx = xsin^{-1}x + \sqrt{1 – x^2} + C\end{array} \)
- \(\begin{array}{l}\int cos^{-1}xdx = xcos^{-1}x – \sqrt{1 – x^2} + C\end{array} \)
- \(\begin{array}{l}\int tan^{-1}x dx = xtan^{-1}x – \frac{1}{2}ln(1 + x^2) + C\end{array} \)
- \(\begin{array}{l}\int cosec^{-1}x dx = x cosec^{-1}x + ln(x + \sqrt{x^2- 1}) + C\end{array} \)
- \(\begin{array}{l}\int sec^{-1}x dx = x sec^{-1}x – ln(x + \sqrt{x^2- 1}) + C\end{array} \)
- \(\begin{array}{l}\int cot^{1}x dx = x cot^{-1}x + \frac{1}{2} ln(1 + x^2) + C\end{array} \)
Hyperbolic functions
Below is the list of integration formulas for hyperbolic functions in maths.
- \(\begin{array}{l}\int sinh\ x dx = cosh\ x + C\end{array} \)
- \(\begin{array}{l}\int cosh\ x dx = sinh\ x + C\end{array} \)
- \(\begin{array}{l}\int tanh\ x dx = ln(cosh\ x) + C\end{array} \)
- \(\begin{array}{l}\int coth\ x dx = ln|sinh\ x| + C\end{array} \)
- \(\begin{array}{l}\int sech\ x dx = tan^{-1}|sinh\ x| + C\end{array} \)
- \(\begin{array}{l}\int cosech\ x dx = ln|tanh\ \frac{x}{2}| + C\end{array} \)
Exponential functions
- ∫ xn dx = ((xn+1)/(n+1))+C ; n≠1
- ∫ ex dx = ex + C
- ∫ ax dx = (ax/ln a) + C ; a > 0, a≠1
Logarithmic functions
- \(\begin{array}{l}\int ln(ax)dx = x\ ln(ax)-x + C\end{array} \)
- \(\begin{array}{l}\int ln(x) = x(ln x – 1) + C\end{array} \)
- \(\begin{array}{l}\int (lnx)^2 dx = x(lnx)^2 – 2x\ lnx + 2x\end{array} \)
- \(\begin{array}{l}\int log_{a}x dx = x\ log_{a}x – \frac{x}{lna} = \frac{x\ lnx – x}{lna}\end{array} \)
- \(\begin{array}{l}\int ln(ax + b)dx = \frac{(ax + b)ln(ax + b) – (ax + b)}{a}\end{array} \)
Integral Formulas for Some Special Functions
As we have already gone through integral formulas for exponential functions, logarithmic functions, trigonometric functions and some basic functions. Let’s have a look at the additional integration formulas, i.e. the integral formulas for some special functions listed below:
- \(\begin{array}{l}\int \frac{1}{(x^2 – a^2)} dx = \frac{1}{2a}.log\left | \frac{(x – a)}{(x + a)} \right | + C\end{array} \)
- \(\begin{array}{l}\int \frac{1}{(a^2 – x^2)} dx = \frac{1}{2a}.log\left | \frac{(a + x)}{(a – x)} \right | + C\end{array} \)
- \(\begin{array}{l}\int \frac{1}{(x^2 + a^2)} dx = \frac{1}{a}tan^{-1}(\frac{x}{a}) + C\end{array} \)
- \(\begin{array}{l}\int \frac{1}{\sqrt{x^2 – a^2}} dx = log|x+ \sqrt{x^2 – a^2}|+ C\end{array} \)
- \(\begin{array}{l}\int \frac{1}{\sqrt{a^2 – x^2}} dx = sin^{-1}(\frac{x}{a})+ C\end{array} \)
- \(\begin{array}{l}\int \frac{1}{\sqrt{x^2 +a^2}} dx = log|x+ \sqrt{x^2 + a^2}|+ C\end{array} \)
Solve Using Integral Formulas
- Calculate ∫ 5x4 dx
- \(\begin{array}{l}\text{Find}\ \int x\sqrt{1+2x}\;dx\end{array} \)
- \(\begin{array}{l}\text{Solve}\ \int \frac{1}{x^{2}+6x+25}\,dx\end{array} \)
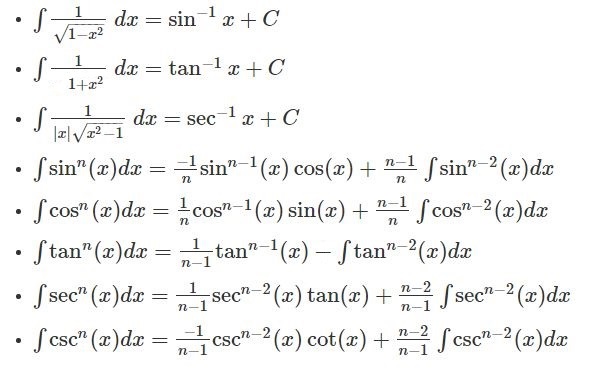
No need of other formula than it
Great job
Very usefull for students
Very good 🙂 I am proud of you:))))
Thank u so much