The area of an isosceles triangle is the amount of region enclosed by it in a two-dimensional space. The general formula for the area of triangle is equal to half the product of the base and height of the triangle. Here, a detailed explanation of the isosceles triangle area, its formula and derivation are given along with a few solved example questions to make it easier to have a deeper understanding of this concept.
Check more mathematics formulas here.
What is the Formula for Area of Isosceles Triangle?
The total area covered by an isosceles triangle is known as its area. For an isosceles triangle, the area can be easily calculated if the height (i.e. the altitude) and the base are known. Multiplying the height with the base and dividing it by 2, results in the area of the isosceles triangle.
What is an isosceles triangle?
An isosceles triangle is a triangle that has any of its two sides equal in length. This property is equivalent to two angles of the triangle being equal. An isosceles triangle has two equal sides and two equal angles. The name derives from the Greek iso (same) and Skelos (leg). An equilateral triangle is a special case of the isosceles triangle, where all three sides and angles of the triangle are equal.

An isosceles triangle has two equal side lengths and two equal angles, the corners at which these sides meet the third side is symmetrical in shape. If a perpendicular line is drawn from the point of intersection of two equal sides to the base of the unequal side, then two right-angle triangles are generated.
| Table of Contents: |
Area of Isosceles Triangle Formula
The area of an isosceles triangle is given by the following formula:
| Area = ½ × base × Height |
Also,
| The perimeter of the isosceles triangle | P = 2a + b |
| The altitude of the isosceles triangle | h = √(a2 − b2/4) |
List of Formulas to Find Isosceles Triangle Area
| Formulas to Find Area of Isosceles Triangle | |
|---|---|
| Using base and Height | A = ½ × b × h
where b = base and h = height |
| Using all three sides | A = ½[√(a2 − b2 ⁄4) × b]
|
| Using the length of 2 sides and an angle between them | A = ½ × a × b × sin(α)
|
| Using two angles and length between them | A = [a2×sin(β)×sin(α)/ 2×sin(2π−α−β)]
|
| Area formula for an isosceles right triangle | A = ½ × a2
a is the measure of equal sides |
How to Calculate Area if Only Sides of an Isosceles Triangle are Known?
If the length of the equal sides and the length of the base of an isosceles triangle are known, then the height or altitude of the triangle is to be calculated using the following formula:
| Altitude of an Isosceles Triangle = √(a2 − b2/4) |
Thus,
| Area of Isosceles Triangle Using Only Sides = ½[√(a2 − b2 /4) × b] |
Here,
- b = base of the isosceles triangle
- h = height of the isosceles triangle
- a = length of the two equal sides
Derivation for Isosceles Triangle Area Using Heron’s Formula
The area of an isosceles triangle can be easily derived using Heron’s formula as explained below.
According to Heron’s formula,
Area = √[s(s−a)(s−b)(s−c)]
Where, s = ½(a + b + c)
Now, for an isosceles triangle,
s = ½(a + a + b)
⇒ s = ½(2a + b)
Or, s = a + (b/2)
Now,
Area = √[s(s−a)(s−b)(s−c)]
Or, Area = √[s (s−a)2 (s−b)]
⇒ Area = (s−a) × √[s (s−b)]
Substituting the value of “s”
⇒ Area = (a + b/2 − a) × √[(a + b/2) × ((a + b/2) − b)]
⇒ Area = b/2 × √[(a + b/2) × (a − b/2)]
Or, area of isosceles triangle = b/2 × √(a2 − b2/4)
Area of Isosceles Right Triangle Formula
| The formula for Isosceles Right Triangle Area= ½ × a2 |
Derivation:
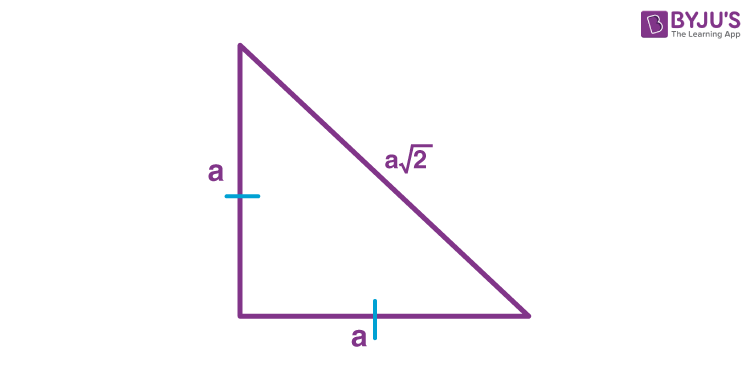
Area = ½ ×base × height
Perimeter of Isosceles Right Triangle Formula
| P = a(2+√2) |
Derivation:
The perimeter of an isosceles right triangle is the sum of all the sides of an isosceles right triangle.
Suppose the two equal sides are a. Using Pythagoras theorem the unequal side is found to be a√2.
Hence, perimeter of isosceles right triangle = a+a+a√2
= 2a+a√2
= a(2+√2)
Area of Isosceles Triangle Using Trigonometry
Using Length of 2 Sides and Angle Between Them
A = ½ × b × c × sin(α)
Using 2 Angles and Length Between Them
A = [c2×sin(β)×sin(α)/ 2×sin(2π−α−β)]
Solved Examples
Example 1:
Find the area of an isosceles triangle given b = 12 cm and h = 17 cm?
Solution:
Base of the triangle (b) = 12 cm
Height of the triangle (h) = 17 cm
Area of Isosceles Triangle = (1/2) × b × h
= (1/2) × 12 × 17
= 6 × 17
= 102 cm2
Example 2:
Find the length of the base of an isosceles triangle whose area is 243 cm2, and the altitude of the triangle is 27 cm.
Solution:
Area of the triangle = A = 243 cm2
Height of the triangle (h) = 27 cm
The base of the triangle = b =?
Area of Isosceles Triangle = (1/2) × b × h
243 = (1/2) × b × 27
243 = (b×27)/2
b = (243×2)/27
b = 18 cm
Thus, the base of the triangle is 18 cm.
Question 3:
Find the area, altitude and perimeter of an isosceles triangle given a = 5 cm (length of two equal sides), b = 9 cm (base).
Solution:
Given, a = 5 cm
b = 9 cm
Perimeter of an isosceles triangle
= 2a + b
= 2(5) + 9 cm
= 10 + 9 cm
= 19 cm
Altitude of an isosceles triangle
h = √(a2 − b2/4)
= √(52 − 92/4)
= √(25 − 81/4) cm
= √(25–81/4) cm
= √(25−20.25) cm
= √4.75 cm
h = 2.179 cm
Area of an isosceles triangle
= (b×h)/2
= (9×2.179)/2 cm²
= 19.611/2 cm²
A = 9.81 cm²
Question 4:
Find the area, altitude and perimeter of an isosceles triangle given a = 12 cm, b = 7 cm.
Solution:
Given,
a = 12 cm
b = 7 cm
Perimeter of an isosceles triangle
= 2a + b
= 2(12) + 7 cm
= 24 + 7 cm
P = 31 cm
Altitude of an isosceles triangle
= √(a2 − b2⁄4)
= √(122−72/4) cm
= √(144−49/4) cm
= √(144−12.25) cm
= √131.75 cm
h = 11.478 cm
Area of an isosceles triangle
= (b×h)/2
= (7×11.478)/2 cm²
= 80.346/2 cm²
Practice Questions
- Find the altitude of the triangle if the length of its base is 25 cm and the area enclosed is 375 cm2?
- The length of the base of an isosceles triangle is half of its altitude. If the altitude of the triangle is 14cm, find the area enclosed by it?
- Find the area of an isosceles triangle, whose length of two equal sides is 5 cm and the length of the third side is 6 cm?
- Find the length of each side of a right isosceles triangle whose area is 112.5 cm2.
Frequently Asked Questions on Area of Isosceles Triangle
What is an Isosceles Triangle?
An isosceles triangle can be defined as a special type of triangle whose 2 sides are equal in measure. For an isosceles triangle, along with two sides, two angles are also equal in measure.
What does the Area of an Isosceles Triangle Mean?
The area of an isosceles triangle is defined as the amount of space occupied by the isosceles triangle in the two-dimensional plane.
What is the Formula for Area of Isosceles Triangle?
To calculate the area of an isosceles triangle, the following formula is used:
A = ½ × b × h
What is the Formula for Perimeter of Isosceles Triangle?
The formula to calculate the perimeter of an isosceles triangle is:
P = 2a + b


Comments