Absolute Value Formula
The absolute value of a number is represented in the form of |a|. This value or number represents the distance between a and 0 on a number line. An absolute value equation is an equation that contains an absolute value expression. The equation for absolute value is mentioned below. There are two forms of absolute value inequalities. One with less than, |a|< b, and the other with greater than, |a|> b. They are solved differently.
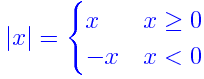
Solved Examples
Question 1: What is the value of 2 | 5x – 1 | if x = – 2?
Solution:
Solution:
2 | 5x – 1 | = 2 | 5 (-2) – 1 |
2 | 5x – 1 | = 2 | -10 – 1 |
2 | 5x – 1 | = 2 | -11 |
2 | 5x – 1 | = 2 × 11
2 | 5x – 1 | = 22
2 | 5x – 1 | = 2 | -10 – 1 |
2 | 5x – 1 | = 2 | -11 |
2 | 5x – 1 | = 2 × 11
2 | 5x – 1 | = 22
Question 2: Solve 4 | x – 2 | = 16
Solution:
4 | x – 2 | = 16
| x – 2 | = 16/4
| x – 2 | = 4
x – 2 = 4 or x – 2 = – 4
x = 4 + 2 or x = – 4 + 2
x = 6 or – 2
Solution:
4 | x – 2 | = 16
| x – 2 | = 16/4
| x – 2 | = 4
x – 2 = 4 or x – 2 = – 4
x = 4 + 2 or x = – 4 + 2
x = 6 or – 2
Comments