Beam Deflection Formula

Deflection is the degree to which a particular structural element can be displaced by a considerable amount of load. It can be referred to as an angle or distance. The distance of deflection of a member under a load is directly related to the slope of the deflected shape of the member under that load. It can be calculated by integrating the function that describes the slope of the member under that load.

The Beam is a long piece of a body capable of holding the load by resisting the bending. The deflection of the beam towards a particular direction when force is applied to it is called Beam deflection.

Based on the type of deflection there are many beam deflection formulas given below,

w = uniform load (force/length units)

V = shear

I = moment of inertia

E = modulus of elasticity

d = deflection

M = moment

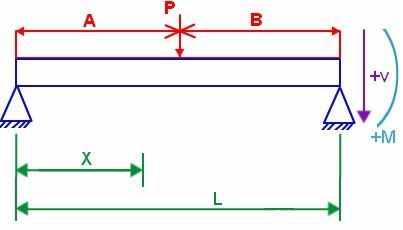
 PINNED-PINNED BEAM WITH UNIFORM LOAD

V = w (L/2 – x)

M = wx/2 (L – x)

δ = wx/24EI (L³ – 2 Lx² + x³)

FIXED-FIXED BEAM WITH UNIFORM LOAD

V = W (L/2 – x)

M = W/12 (6Lx – L² – 6x²)

δ = wx²/24EI (L – x)²

PINNED-FIXED BEAM WITH UNIFORM LOAD

V = w(3L/8 – x)

M = wx (3L/8 – x/2)

δ = wx/48EI (L³ – 3Lx² + 2x³)

FREE-FIXED BEAM WITH UNIFORM LOAD

V = – wx

M = – wx²/2

δ = w/24EI (x⁴ – 4L³x + 3L⁴)

PINNED-PINNED BEAM WITH POINT LOAD

V = Pb/L – P (x-a)⁰

M = Pbx/L – P (x-a)¹

δ = P/6EI [bx3/L – abx/L (2L – a) – (x – a)³]

FIXED-FIXED BEAM WITH POINT LOAD

V = Pb²/L³ (L + 2a) – P(x – a)⁰

M = −Pab²/L² + Pb²x/L3 (L + 2a) – P (x – a)¹

δ = P/6EI [b²x³/L³ (L + 2a) – 3ab2x2/L2 – (x – a)³]

PINNED-FIXED BEAM WITH POINT LOAD

V = Pb²/2L³ (2L + a) – P(x – a)⁰

M = Pb²x/2L³(2L + a) – P (x – a)¹

δ = P/6EI[b²x³/2L³ (2L + a) – 3ab²x/2L – (x – a)³]

FREE-FIXED BEAM WITH POINT LOAD

V = -P(x – a)⁰

M = -P(x – a)¹

δ = P/6EI [3b²x – 2L³ – a³ – (x – a)³]

Solved Examples

Example 1

A pinned-pinned beam of length 50 cm is put under uniform load of 60 gms having x as 5 cm. Determine the shear.

Solution:

Given parameters are

Length L = 50 cm

Uniform load w = 60 gms

Displacement x = 5 cm

The shear is given by V = w (L/2 – x)

= 0.06 kg (0.5/2 m – 0.05 m)

= 0.06 kg (0.25 – 0.05)m

= 0.012 kgm.

Question 2: n fixed-fixed beam of length 30 cm is put under a uniform load of 200 gm having x as 20 cm. Determine the moment.

Solution:

Given parameters are

Length L = 30 cm,

Uniform load w = 200 gms,

Displacement x = 20 cm

The moment is

V = −wx²/2

= −0.2kg×0.2² / 2

= 0.004 kg m².