De Morgan’s First Law states that the complement of the union of two sets is the intersection of their complements. Whereas De Morgan’s second law states that the complement of the intersection of two sets is the union of their complements. These two laws are called De Morgan’s Law. De Morgan’s first law can be expressed as (AUB)’ = A’∩B’. In set theory, these laws relate the intersection and union of sets by complements. In this article, we will learn De Morgan’s first law statement and proof with many solved examples in detail.
Table of Contents:
De Morgan’s First Law Statement and Proof
A well-defined collection of objects or elements is known as a set. Various operations like complement of a set, union and intersection can be performed on two sets. These operations and their usage can be further simplified using a set of laws known as De Morgan’s Laws. These are very easy and simple laws.
Any set consisting of all the objects or elements related to a particular context is defined as a universal set. Consider a universal set U such that A and B are the subsets of this universal set.
According to De Morgan’s first law, the complement of the union of two sets A and B is equal to the intersection of the complement of the sets A and B.
(A∪B)’= A’∩ B’ —–(1)
Where complement of a set is defined as
A’= {x:x ∈ U and x ∉ A}
Where A’ denotes the complement.
This law can be easily visualized using Venn Diagrams.
The L.H.S of equation 1 represents the complement of the union of two sets A and B. First of all, the union of two sets A and B is defined as the set of all elements which lie either in set A or in set B. It can be visualized using Venn Diagrams as shown:
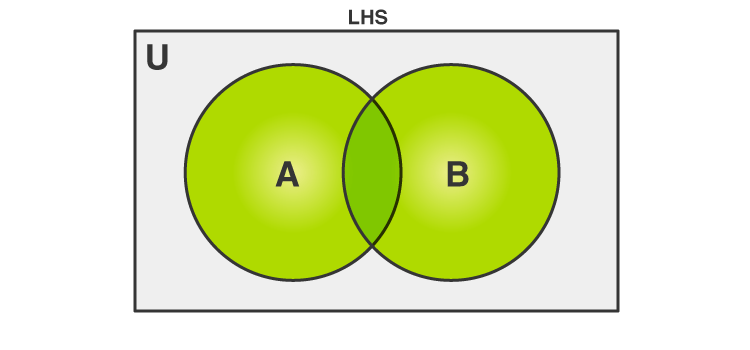
Figure 1 Union of Sets
The highlighted or the green colored portion denotes A∪B. The complement of union of A and B i.e., (A∪B)’is set of all those elements which are not in A∪B. This can be visualized as follows:
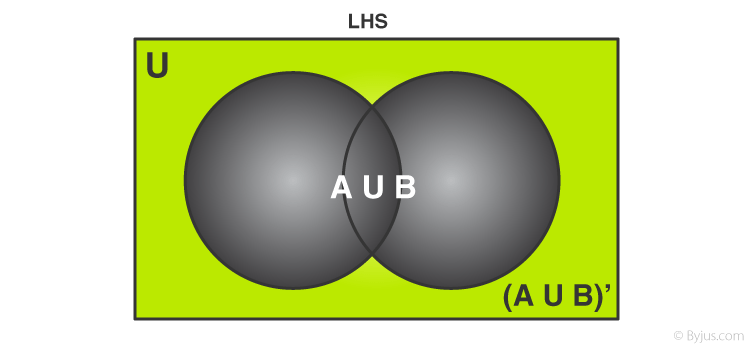
Figure 2 Complement of sets
Similarly, R.H.S of equation 1 can be represented using Venn Diagrams as well, the first part i.e., A’ can be depicted as follows:
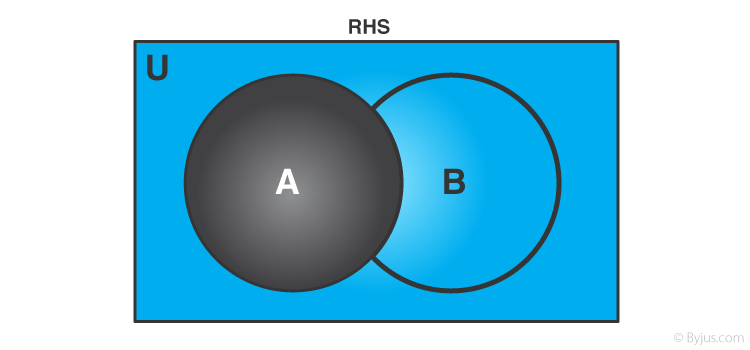
Figure 3 Complement of set A
The portion in black indicates set A and the blue part denotes its complement i.e., A’.
Similarly, B’ is represented as:

Figure 4 Complement of set B
The portion in black indicates set B and the yellow part denotes its complement i.e., B’.
If fig. 3 and 4 are superimposed on one another, we get the figure similar to that of the complement of sets.
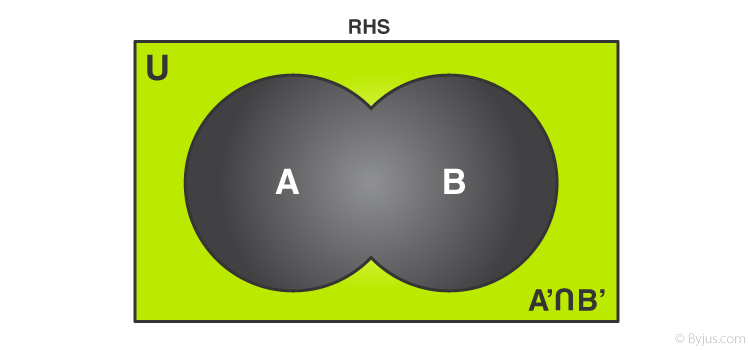
Figure 5 Intersection of complements of sets
Hence L.H.S = R.H.S
Mathematically,
As A∪B = either in A or in B
(A∪B)’= L.H.S = neither in A nor in B
Also, A’= Not in A
B’= Not in B
A’∩ B’= Not in A and not in B
⇒(A∪B)’= A’∩ B’
Thus, by visualizing the Venn Diagrams and analyzing De Morgan’s Laws by writing them down, their validity can be justified.
| Also, read: |
Solved Examples of De Morgan’s First Law
Example 1:
Let U = {1, 2, 3, 4, 5, 6, 7, 8}, A ={3, 4, 5}, B = {4, 5, 6}. Show that (AUB)’ = A’∩B’.
Solution:
Given that:
U = {1, 2, 3, 4, 5, 6, 7, 8}
A = {3, 4, 5}
B = {4, 5, 6}
We know that, Demorgan’s first law is (AUB)’ = A’∩B’.
L.H.S:
AUB = {3, 4, 5} U {4, 5, 6}
AUB = {3, 4, 5, 6}
Hence, (AUB)’ = {1, 2, 7, 8}
R.H.S:
We know that A = {3, 4, 5}
Hence, A’ = {1, 2, 6, 7, 8}
Similarly, B = {4, 5, 6}
Thus, B’ = {1, 2, 3, 7, 8}
Therefore, A’∩B’ = {1, 2, 6, 7, 8} ∩ {1, 2, 3, 7, 8}
A’∩B’ = {1, 2, 7, 8}
Thus, L.H.S = R.H.S
Hence, (AUB)’ = A’∩B’ is proved.
Example 2:
If U = {a, b, c, d, e, f, g, h}, P = {a, c, d}, Q = {a, b, f, g}. Prove the Demorgan’s first law.
Solution:
Given:
U = {a, b, c, d, e, f, g, h}
P = {a, c, d}
Q = {a, b, f, g}
According to Demorgan’s first law, we have to prove, (PUQ)’ = P’∩Q’
To prove (PUQ)’:
PUQ = {a, c, d} U {a, b, f, g}
PUQ = {a, b, c, d, f, g}
Hence, (PUQ)’ = {e, h}
To prove P’∩Q’:
Given that P = {a, c, d}
Hence, P’ = {b, e, f, g, h}
Also given that, Q = {a, b, f, g}
Q’ = {c, d, e, h}
Hence, P’∩Q’ = {b, e, f, g, h} ∩ {c, d, e, h} = {e, h}
Hence, (PUQ)’ = P’∩Q’ is proved.
De Morgan’s First Law Practice Questions
Solve the following problems:
- Prove the Demorgan’s first law if U = {11, 12, 13, 14, 15, 16, 17}, A = {11, 12, 13, 15}, and B = {13, 15, 16, 17}.
- Let U = {p, q, r, s, t, u, v, w}, A = {p, r, s, t} and B = {t, v, w}. Show that (AUB)’ = A’∩B’.
Stay tuned to BYJU’S – The Learning App and download the app to explore all Maths-related articles.
Frequently Asked Questions on De Morgan’s First Law
What does De Morgan’s first law state?
De Morgan’s first law states that the complement of the union of two sets A and B is equal to the intersection of the complement of the sets A and B.
How to express De Morgan’s first law?
If A and B are the two sets, then De Morgan’s first law is expressed as (AUB)’= A’∩B’.
What is De Morgan’s first law in boolean algebra?
In boolean algebra, De Morgan’s first law states that “if two (or more) input variables are AND’ed and negated, it should be equivalent to the OR of the complements of the individual input variables”.

Good graphic method
Hello Sir
Please answer these questions for me i really need it right now.
Question 1: Prove the DeMorgan law A={1,2,3,4), B=(3,4,5,6}?
Question 2: Find the Power set of A={0,1,2,3,4,5,6}
with full written answer
Thank You
Sir I have a question.
Please help
Change it into de Morgan’s law:
The fan is slow or it is very hot.
VERY GOOD APP FOR STUDYING IN FUTURE AND IN PRESENT TIMES.