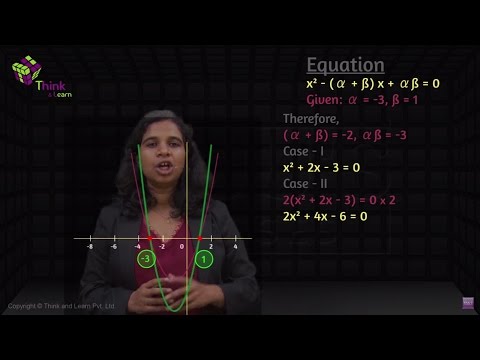
Quadratic Equation: Sum and Product of Roots:
A general quadratic equation is given by \(ax^2~+~bx~+~c~=~0\)
\(x~=~\frac{-b~±~\sqrt{b^2~-~4ac}}{2a}\)
\(\Rightarrow~x~=~-\frac{b}{2a}~±~\frac{\sqrt{b^2~-~4ac}}{2a}\)
The term \(b^2~-~4ac\)
\(\Rightarrow~x~=~-\frac{b}{2a}~±~\frac{\sqrt{D}}{2a}\)
If the roots of this equation are given by \(α\)
\(α~+~β~=~-\frac{b}{a}\)
\(αβ~=~\frac{c}{a}\)
Sum of Roots
Thus, the sum of roots of a quadratic equation is given by the negative ratio of coefficient of \(x\)
Let us try to prove this graphically.
We know that the graph of a quadratic function is represented using a parabola. If α and β are the real roots of a quadratic equation, then the point of intersection of the plot of this function with x-axis represents its roots.
Let us assume that \(\frac{\sqrt{D}}{2a}~=~n\)
\(α~=~-\frac{b}{2a-n}\)
\(β~=~-\frac{b}{2a+n}\)
Graphically, it can be shown as:
Adding equations (1) and (2), we get
\(α~+~β~=~-\frac{2b}{2a}\)
\(⇒α~+~β~=~-\frac{b}{a}\)
Also,
\(α~=~\frac{-b~-~\sqrt{b^2~-~4ac}}{2a}\)
\(β~=~\frac{-b~+~\sqrt{b^2~-~4ac}}{2a}\)
Multiplying both these equations we get
\(αβ~=~\frac{-b~-~\sqrt{b^2~-~4ac}}{2a}~\times~\frac{-b~+~\sqrt{b^2~-~4ac}}{2a}\)
\(⇒~αβ~=\frac{(-b)^2~-~(b^2~-~4ac)}{4a^2}\)
\(⇒αβ~=~\frac{c}{a}\)
Consider the general form of quadratic equation \(ax^2~+~bx~+~c~=~0\)
Dividing both sides by \(‘a’\)
\(\frac{a}{a}~x^2~+~\frac{b}{a}~x~+~\frac{c}{a}~=~0\)
\(⇒~x^2~+~\frac{b}{a} ~x~+\frac{c}{a}~=~0\)
Since,
\(α~+~β~=~-\frac{b}{a}\)
\(αβ~=~\frac{c}{a}\)
\(⇒~x^2~-~(α~+~β)~x~+~αβ~=~0\)
Thus by using roots, the equation can be obtained.
Consider the following two equations:
\(x^2~+~2x~-~3~=~0\)
The roots of these equations are equal i.e. 1 and -3. Graphically, these equations intersect thex-axis at the same points as shown below.
If the coefficients of two quadratic equations having same roots is given by \(a_1,b_1,c_1\)
\(\frac{a_1}{b_1}~ =~\frac{a_2}{b_2}~ =~\frac{c_1}{c_2}\)
The relationship between roots and coefficients of an equation can be established for higher order equations too. We know that the degree specifies how many roots an equation can have. The number of roots of an equation is equal to its degree. Let us take an \(n^{th}\)
For a function \(f(x)~=~a_n x^n~+~a_{n-1}~ x^{n-1}~+⋯..+~a_1 x~+~a_0\)
then, \(f(x)~=~α_n (x~-~α_{n-1})(x-α_{n-2})………(x-α_0)\)
\(⇒a_n x^n~+~a_{n-1} x^{n-1}~+⋯..~+~a_1 x~+~a_0~=~α_n (x~-~α_{n-1})(x~-~α_{n-2})………(x-α_0)\)
On comparing coefficients of \(x^{n-1}\)
\(S_1~=~α_{n-1}~+~α_{n-2}~+~⋯~+~α_0~=~∑_{i=0}^{n-1}α_i ~=~-\frac{a_{n-1}}{a_n}~ =~(-1)^1\)
On comparing coefficients of \(x^{n-2}\)
\(S_2~=~(α_{n-1})(α_{n-2})~+~(α_{n-2})(α_{n-3})~+~⋯~=~\sum\limits_{i~\neq~j}{α_iα_j}~=~\frac{a_{n-2}}{a_n}~ =~(-1)^{2}\frac{coefficient~ of~x^{n-2}}{coefficient~ of~x^n}\)
On comparing coefficients of \(x^{n-3}\)
\(S_2~=~(α_{n-1})(α_{n-2})(α_{n-3})~+~(α_{n-2})(α_{n-3})(α_{n-4})~+~⋯~=~\sum\limits_{i≠j≠k}{α_i α_j α_k}\)
=\(-\frac{a_{n-3}}{a_n}~ =~(-1)^3 ~\frac{coefficient~ of~x^{n-3}}{coefficient ~of~x^n}\)
Similarly,
\(S_n~=~(α_{n-1})(α_{n-2})(α_{n-3})~…~α_0~=~(-1)^n~\frac{a_0}{a_n}~ =~(-1)^n~\frac{constant~ term}{coefficient ~of~x^n}\)
Thus, for a quadratic equation of the form \(ax^2~+~bx~+~c~=~0\)
\(α~+~β~=~-\frac{b}{a}\)
\(αβ~=~\frac{c}{a}\)
For cubic equation of the form \(ax^3~+~bx^2~+~cx~+~d~=~0\)
\(α~+~β~+~γ~=~-\frac{b}{a}\)
\(αβ~+~βγ~+~γα~=~\frac{c}{a}\)
\(αβγ~=~-\frac{d}{a}\)
For a fourth degree equation known as quartic equation in general form is given by:
\(ax^4~+~bx^3~+~cx^2~+~dx~+~e~=~0\)
If its roots are \(α,β,γ\)
\(α~+~β~+~γ~+~δ~=~-\frac{b}{a}\)
\(αβ~+~αγ~+~αδ~+~βγ~+~γδ~+~δβ~=~\frac{c}{a}\)
\(αβγ~+~βγδ~+~γδα~+~αβδ~=~-\frac{d}{a}\)
\(αβγδ~=~\frac{e}{a}\)
Thus, this process can be continued to find out the relationship between the roots and the coefficients of any equation of \(n^{th}\)
