What is a Unit Cell?
The smallest repeating unit of the crystal lattice is the unit cell, the building block of a crystal.
The unit cells which are all identical are defined in such a way that they fill space without overlapping. The 3D arrangement of atoms, molecules or ions inside a crystal is called a crystal lattice. It is made up of numerous unit cells. One of the three constituent particles takes up every lattice point.
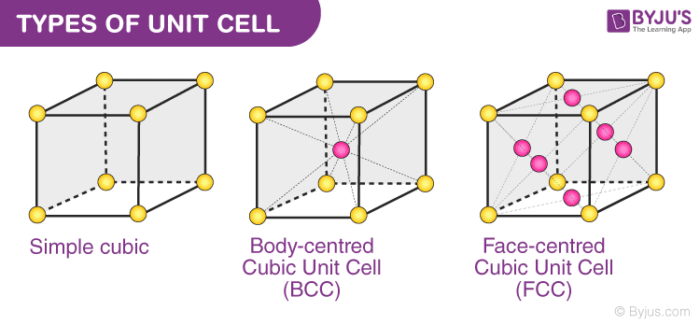
A unit cell can either be primitive cubic, body-centred cubic (BCC) or face-centred cubic (FCC). In this section, we will discuss the three types of unit cell in detail.
Table of Contents
- Types of Unit Cell
- Recommended Videos
- Primitive Cubic Unit Cell
- Body centred Cubic Unit Cell
- Face centred Cubic Unit Cell
- Volume of HCP Unit Cell
- Frequently Asked Questions – FAQs
Types of Unit Cell
Numerous unit cells together make a crystal lattice. Constituent particles like atoms and molecules are also present. Each lattice point is occupied by one such particle.
- Primitive Cubic Unit Cell
- Body-centered Cubic Unit Cell
- Face centered cubic unit cell
Recommended Videos
Face-Centred Cubic Unit cell (FCC)

Types of Unit Cells

1. Primitive Cubic Unit Cell
In the primitive cubic unit cell, the atoms are present only at the corners. Every atom at the corner is shared among 8 adjacent unit cells. There are 4 unit cells in the same layer and 4 in the upper (or lower) layer. Therefore, a particular unit cell has only 1/8th of an atom. Each small sphere in the following figure represents the centre of a particle that occupies that particular position and not its size. This structure is known as an open structure.
- The atoms in the primitive cubic unit cell are present only at the corners
- Every atom at the corner is shared among eight adjacent unit cells
- Four unit cells are present in the same layer
- Four unit cell in the upper/lower layer
- Therefore, a particular unit cell has the only 1/8th of an atom
- Each small sphere in the following figure represents the centre of a particle which occupies that particular position and not its size
Below is an open structure

In each cubic unit cell, there are 8 atoms at the corners. Therefore, the total number of atoms in one unit cell is
2. Body-centred Cubic Unit Cell (BCC)
A BCC unit cell has atoms at each corner of the cube and an atom at the centre of the structure. The diagram shown below is an open structure. According to this structure, the atom at the body centre wholly belongs to the unit cell in which it is present.
- In BCC unit cell every corner has atoms.
- There is one atom present at the centre of the structure
- Below diagram is an open structure
- According to this structure atom at the body centres wholly belongs to the unit cell in which it is present.
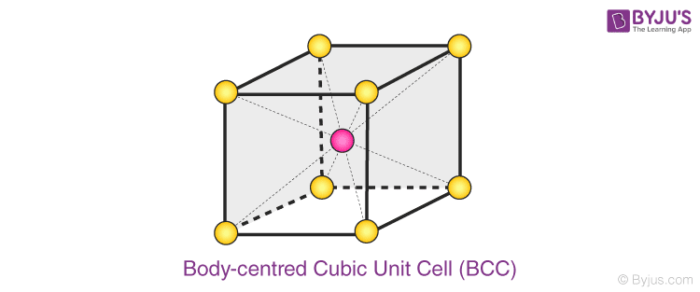
Body centred Cubic (BCC) Unit Cell
Number of Atoms in BCC Cell:
Thus, in a BCC cell, we have:
- 8 corners × 1/8 per corner atom = 8 × 1/8 = 1 atom
- 1 body centre atom = 1 × 1 = 1 atom
Therefore, the total number of atoms present per unit cell = 2 atoms.
Solved Example
Question:
Lithium metal crystallizes in a body centered cubic crystal. If the length of the side of the unit cell of lithium is 351pm, the atomic radius of the lithium will be
Solution:
In case of body centered cubic (BCC) crystal,
Hence, atomic radius of lithium
= 151.98
3. Face-centred Cubic Unit Cell (FCC)
An FCC unit cell contains atoms at all the corners of the crystal lattice and at the centre of all the faces of the cube. The atom present at the face-centered is shared between 2 adjacent unit cells and only 1/2 of each atom belongs to an individual cell.
- In FCC unit cell atoms are present in all the corners of the crystal lattice
- Also, there is an atom present at the centre of every face of the cube
- This face-centre atom is shared between two adjacent unit cells
- Only 12 of each atom belongs to a unit cell
The diagram shown below is an open structure.

Number of Atoms in BCC Cell
a) 8 corners × 1/8 per corner atom = 8 × 1/8 = 1 atom
b) 6 face-centered atoms × 1/2 atom per unit cell = 3 atoms
Hence, the total number of atoms in a unit cell = 4 atoms
Thus, in a face-centred cubic unit cell, we have:
- 8 corners × 1/8 per corner atom = 8 × 1/8 = 1 atom
- 6 face-centred atoms × 1/2 atom per unit cell = 3 atoms
Therefore, the total number of atoms in a unit cell = 4 atoms.
Volume of HCP Unit Cell
A unit cell is the smallest representation of an entire crystal. The hexagonal closest packed (HCP) has a coordination number of 12 and contains 6 atoms per unit cell. The face-centered cubic (FCC) has a coordination number of 12 and contains 4 atoms per unit cell.
Volume = area of base × height
Frequently Asked Questions – FAQs
What is unit cell and its types?
The smallest replicating portion of a crystal lattice is a unit cell. Unit cells exist in many types. The cubic crystal structure, for example, consists of three distinct unit cell types : (1) plain cubic, (2) face-centered cubic, and (3) body-centered cubic.
What is meant by unit cell of crystal?
The unit cell is defined as the smallest repeated unit with full crystal structure symmetry. The unit cell geometry is known as a parallelepiped, providing six lattice parameters taken as the lengths of the edges of the cells (a, b , c) and the angles between them (α, β, ÿ).
How many kinds of primitive unit cells are possible?
Seven simple crystal structures exist; cubic, tetragonal, orthorhombic, hexagonal, monoclinic, triclinic, and rhombohedral. They differ in the way their crystallographic axes and angles are arranged. Bravis defined 14 possible crystal systems according to the above seven.
What do you mean by primitive unit cell?
A primitive cell (also known as a primitive unit cell) is a minimum-volume unit cell in mathematics, biology, mineralogy (especially crystallography), and solid state physics, referring to a single lattice point of a structure with discrete translation symmetry. The main cell is simple.
What is hcp unit cell?
In a unit cell, the number of coordinates of an atom is the number of atoms that it touches. The closest hexagonal packed (hcp) has a coordinating number of 12 and contains six atoms per unit cell. The face-centered cubic (fcc) has a total of 12 coordinates and contains 4 atoms per unit cell.
To learn more about crystal lattices and solid-state chemistry, download BYJU’S – The Learning App.


Comments