In trigonometry, the law of cosines is also known as the cosine formula or cosine rule, relates the lengths of the sides of a triangle to the cosine of one of its angles.
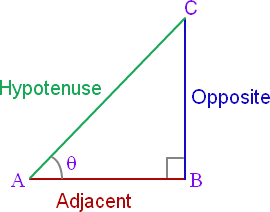
Formula for Cosine
The Cosine Formula is,
cos θ=Adjacent/Hypotenuse
- a2 = b2 + c2 − 2bc.cosA
- b2 = a2 +c2 − 2ac.cosB
- c2 = a2 + b2 − 2ab.cosC
Solved Examples
Question 1: Calculate the cosine angle of a right triangle given the adjacent side and hypotenuse are 12 cm and 15 cm respectively ?
Solution:
Solution:
Given,
Adjacent side = 12 cm
Hypotenuse = 15 cmcos θ = Adjacent/Hypotenuse
Hypotenuse = 15 cmcos θ = Adjacent/Hypotenuse
cos θ = 12 cm/15 cm
cos θ = 0.8

Comments