Diameter Formula
Diameter is defined as the line passing through the center of a circle having two extremes on the circumference of a circle.
The Diameter of a circle divided the circle into two equal parts known as semi-circle.
The center of a circle is the midpoint of its diameter. It divides the diameter into two equal parts, each of which is a radius of the circle. The radius is half the diameter.
We all know that A chord of a circle is a straight line segment whose endpoints both lie on the circle. Thus it can be said that the diameter is the longest possible chord on any circle.
Relation between Radius and Diameter:
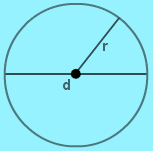
We know that the the distance from the center point to any point on the circumference of a circle is a fixed distance, known as the Radius of a circle.
Therefore, the relation between Radius and Diameter is
Formula for Area and circumference in Terms of Diameter:
Circumference:
We know
Circumference =
It can be re-written as,
=
Area:
We know
Area=
It can be re-written as
|
Let’s Work Out- Example: Find the diameter of the circle whose radius is 8 cm ? Also find the Area of a circle. Solution: Given, Radius of the circle (r) = 8 cm Diameter of the circle = 2r = = 16 cm Now Area \(\begin{array}{l}\frac{\pi }{4}.d^{2}\end{array} \)
\(\begin{array}{l}\frac{\pi }{4}.16^{2}\end{array} \)
= 200.96 cm2
Example: Find the diameter of the circle whose Area is 154cm2? Also, find the circumference of the circle. (Take Solution: Given, Area of the circle (A) = 154cm2 We know Area (A) =
\(\begin{array}{l}\Rightarrow 154=\frac{22}{7.4}.d^{2}\end{array} \)
\(\begin{array}{l}\Rightarrow d^{2}=7^{2}.4=7^{2}.2^{2}\end{array} \)
Now Finding the Circumference of a circle which is equal to, \(\begin{array}{l}C=\pi d\end{array} \)
\(\begin{array}{l}=\frac{22}{7} \times 14 \end{array} \)
= 44 cm |
Comments