In Mathematics, it is required to convert the units while solving many problems. To carry out the required calculations, mathematical conversions are needed. For example, to find the area of a triangle, if a base is given in cm, and height is given in meter, and you are asked to find the area of a triangle in cm, it is necessary to convert the height in meters into centimetres. Therefore, it is required to know the conversion of units to convert a unit into the required unit.
What is Conversion of Units?
The use of a unit depends on the situation, such as the area of a room is expressed in meters, but the length of a pencil is expressed in centimetres and its thickness in mm.
Thus, we need to convert one unit to another. Before understanding the concept of conversion of units, we need to understand the relationship between units.
Length and Mass conversion
Mensuration is an ancient concept. Every physical quantity, like length, mass, time, temperature etc., have a specific unit. By definition, a unit is a magnitude of a physical quantity.
There are two systems of units:

- SI units (International System of Units)
- Metric system
For example, the SI unit of length is a metre (m), while metric units are kilometre (km), meter (m), decimetre (dm), centimetre (cm) and millimetre (mm).
SI unit of mass is Kilograms (kg).
Importance of Mathematical Conversions
In order to have accuracy and avoid confusion in measurement, we need to convert one unit to another. For instance, we do not measure the length of a pencil in kilometres. In such a case, one has to convert kilometre (km) to centimetre (cm). Generally, the conversion of one unit to another unit of the same quantity is performed using multiplicative conversion factors. Let’s see how to convert a different unit of length and mass.
Table for Length Conversion
The conversion of units related to length can be represented as:
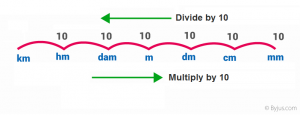
The length conversion is given in the figure above. The relation between the adjacent unit varies by the multiple of 10 (moving left to the right) and vice-versa (i.e. moving right to the left).
The table for conversion of length is:
| Unit conversion for Length | |
| 1 millimeter | 0.001 meter |
| 1 centimeter | 0.01 meter |
| 1 decimeter | 0.1 meter |
| 1 decameter | 10 meters |
| 1 hectometer | 100 meters |
| 1 kilometer | 1000 meters |
| 1 inch | 2.54 × 10−2 meters |
| 1 foot | 0.3048 meters |
| 1 mile | 1.609344 km |
| Example: Convert 2 mm to dam.
Solution: Given 2 mm length. From the length conversion table, we see dam is 4th position left to mm. Thus, dividing the given length by 104. ⇒ 2 mm = 2/104 dam ⇒ 2 mm = 0.0002 dam |
Table for Mass Conversion
The conversion of mass or weight can be done as shown in the below figure.
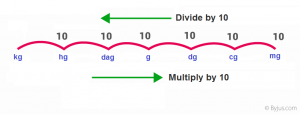
The below table helps to understand the convection of units for mass.
| Unit conversion for Mass | |
| 1 milligram | 0.001 gram |
| 1 centigram | 0.01 gram |
| 1 decigram | 0.1 gram |
| 1 decagram | 10 gram |
| 1 hectogram | 100 gram |
| 1 kilogram | 1000 grams |
Unit Conversion Table
Let’s have a look at some basic unit conversion of mass and length.
| Units of Length | Units of Mass |
|---|---|
| 1 km = 10 hm
= 100 dam = 1000 m |
1 kg = 10 hg
= 100 dag = 1000 g |
| 1m = 10 dm
= 100 cm = 1000 mm |
1 g = 10 dg
= 100 cg = 1000 mg |
| 1 dm = 10 cm
= 100 mm |
1 dg = 10 cg
= 100 mg |
| 1 cm = 10 mm | 1 cg = 10 mg |
From the table above, we have seen values of units of length are not the same, i.e. 1 km ≠ 1m. When 1 km is equal to 1000 m, we need 1000 meters to make up one kilometre. This makes a kilometre a bigger unit than a meter. This is same for 1 kg = 1000g. Conversion of units can be done in a few steps.
In mathematics, we also come across time-related problems, for example, simple and compound interest, speed and distance, work, etc.
The below table shows the conversion of units for time.
| Conversion of Units for Time | |
| 1 minute | 60 seconds |
| 1 hour | 60 minutes (or) 3600 seconds |
| 1 day | 24 hours |
| 1 week | 7 days |
| 1 year | 365 days |
In geometry, we deal with many problems of finding the area and perimeter of shapes. In such cases, one may need to convert the units of measure of area. The below table helps in such types of conversions.
| Conversion of Units for Area | |
| 1 sq. inch | 6.4516 x 10-4 square meter |
| 1 sq. foot | 9.2903 x 10-2 square meter |
| 1 acre | 4.0468 x 103 square meter |
| 1 hectare | 1 x 104 square meter |
| 1 sq. mile | 2.5888 x 106 square meter |
Points to remember:
- To convert bigger units to a smaller unit multiply.
- To convert a smaller unit to a bigger unit divide.
Conversion of Units Solved Examples
| Example 1: Convert 2 cm to km.
Step 1: Draw a line or box as shown below,
Step 2: Put 1 at the larger unit to be converted. Here we want to convert cm to km, Since km is the larger unit, thus put 1 under the corresponding column (km).
Step 3: Now put 0 till the smaller unit. Here we want to convert cm to km, put 0 till the corresponding smaller unit.
We see the conversion is from a smaller to a larger unit. Thus, we need to divide the given length by 100000 (i.e. 105). 2cm = 2/105 km ⇒2cm = 0.00002 km Example 2: Convert 5 grams to milligrams. Solution: We have to convert 5 grams to milligrams. We know, 1 g = 1000 mg Thus, 5 g = 5 × 1000 = 5000 mg |
To solve more problems on the topic, download BYJU’S – The Learning App and watch interactive videos. Also, take free tests to practice for exams.


Comments