In Geometry, a triangle is a three-sided polygon that consists of three edges and three vertices. The most important property of a triangle is that the sum of the internal angles of a triangle is equal to 180 degrees. This property is called angle sum property of triangle.
If ABC is a triangle, then it is denoted as ∆ABC, where A, B and C are the vertices of the triangle. A triangle is a two-dimensional shape, in Euclidean geometry, which is seen as three non-collinear points in a unique plane.
| Table of contents: |
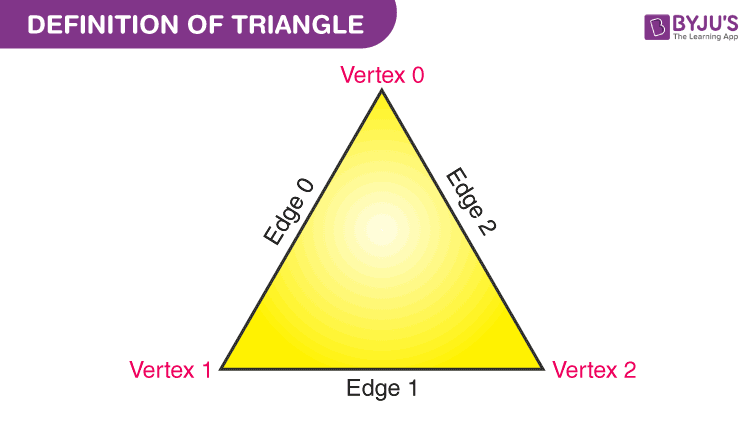
Below given is a triangle having three sides and three edges, which are numbered as 0,1,2.
Definition
As we discussed in the introduction, a triangle is a type of polygon, which has three sides, and the two sides are joined end to end is called the vertex of the triangle. An angle is formed between two sides. This is one of the important parts of geometry.
Some major concepts, such as Pythagoras theorem and trigonometry, are dependent on triangle properties. A triangle has different types based on its angles and sides.
Shape of Triangle
Triangle is a closed two-dimensional shape. It is a three-sided polygon. All sides are made of straight lines. The point where two straight lines join is the vertex. Hence, the triangle has three vertices. Each vertex forms an angle.
Angles of Triangle
There are three angles in a triangle. These angles are formed by two sides of the triangle, which meets at a common point, known as the vertex. The sum of all three interior angles is equal to 180 degrees.
If we extend the side length outwards, then it forms an exterior angle. The sum of consecutive interior and exterior angles of a triangle is supplementary.
Let us say, ∠1, ∠2 and ∠3 are the interior angles of a triangle. When we extend the sides of the triangle in the outward direction, then the three exterior angles formed are ∠4, ∠5 and ∠6, which are consecutive to ∠1, ∠2 and ∠3, respectively.
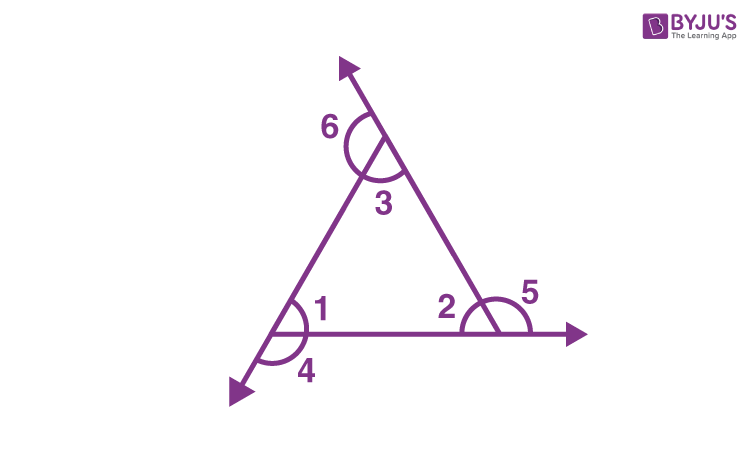
Hence,
∠1 + ∠4 = 180° ……(i)
∠2 + ∠5 = 180° …..(ii)
∠3 + ∠6 = 180° …..(iii)
If we add the above three equations, we get;
∠1+∠2+∠3+∠4+∠5+∠6 = 180° + 180° + 180°
Now, by angle sum property we know,
∠1+∠2+∠3 = 180°
Therefore,
180 + ∠4+∠5+∠6 = 180° + 180° + 180°
∠4+∠5+∠6 = 360°
This proves that the sum of the exterior angles of a triangle is equal to 360 degrees.
Properties
Each and every shape in Maths has some properties which distinguish them from each other. Let us discuss here some of the properties of triangles.
- A triangle has three sides and three angles.
- The sum of the angles of a triangle is always 180 degrees.
- The exterior angles of a triangle always add up to 360 degrees.
- The sum of consecutive interior and exterior angle is supplementary.
- The sum of the lengths of any two sides of a triangle is greater than the length of the third side. Similarly, the difference between the lengths of any two sides of a triangle is less than the length of the third side.
- The shortest side is always opposite the smallest interior angle. Similarly, the longest side is always opposite the largest interior angle.
Also, read:
Types
On the basis of length of the sides, triangles are classified into three categories:
- Scalene Triangle
- Isosceles Triangle
- Equilateral Triangle
On the basis of measurement of the angles, triangles are classified into three categories:
- Acute Angle Triangle
- Right Angle Triangle
- Obtuse Angle Triangle
Scalene Triangle
A scalene triangle is a type of triangle, in which all the three sides have different side measures. Due to this, the three angles are also different from each other.

Isosceles Triangle
In an isosceles triangle, two sides have equal length. The two angles opposite to the two equal sides are also equal to each other.
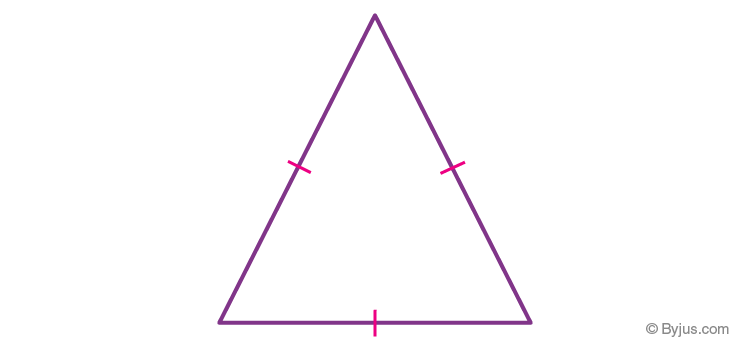
Equilateral Triangle
An equilateral triangle has all three sides equal to each other. Due to this all the internal angles are of equal degrees, i.e. each of the angles is 60°
Acute Angled Triangle
An acute triangle has all of its angles less than 90°.
Right Angled Triangle
In a right triangle, one of the angles is equal to 90° or right angle.
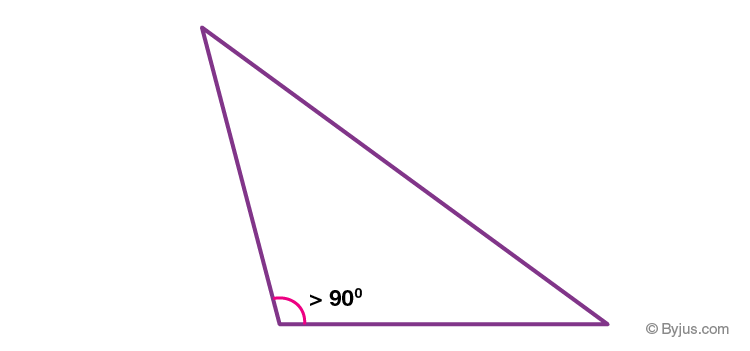
Obtuse Angled Triangle
An obtuse triangle has any of its one angles more than 90°.
Perimeter of Triangle
A perimeter of a triangle is defined as the total length of the outer boundary of the triangle. Or we can say, the perimeter of the triangle is equal to the sum of all its three sides. The unit of the perimeter is same as the unit of sides of the triangle.
| Perimeter = Sum of All Sides |
If ABC is a triangle, where AB, BC and AC are the lengths of its sides, then the perimeter of ABC is given by:
Area of a Triangle
The area of a triangle is the region occupied by the triangle in 2d space. The area for different triangles varies from each other depending on their dimensions. We can calculate the area if we know the base length and the height of a triangle. It is measured in square units.
Suppose a triangle with base ‘B’ and height ‘H’ is given to us, then, the area of a triangle is given by-

Formula:
| Area of triangle = Half of Product of Base and Height
Area = 1/2 × Base × Height |
Example
Question- Find the area of a triangle having base equal to 9 cm and height equal to 6 cm.
Solution- We know that Area = 1/2 × Base × Height
= 1/2 × 9 × 6 cm2
= 27 cm2
Area of Triangle Using Heron’s Formula
In case, if the height of a triangle is not given, we cannot be able to use the above formula to find the area of a triangle.
Therefore, Heron’s formula is used to calculate the area of a triangle, if all the sides lengths are known.
First, we need to calculate the semi perimeter (s).
s = (a+b+c)/2, (where a,b,c are the three sides of a triangle)
Now Area is given by; A = √[s(s-a)(s-b)(s-c)]
Solved Examples
Question 1: If ABC is a triangle where AB = 3cm, BC=5cm and AC = 4cm, then find its perimeter.
Solution: Given, ABC is a triangle.
AB = 3cm
BC = 5cm
AC = 4cm
As we know by the formula,
Perimeter = Sum of all three sides
P = AB + BC + AC
P = 3+5+4
P = 12cm
Question 2: Find the area of a triangle having sides 5,6 and 7 units length.
Solution- Using Heron’s formula to find the area of a triangle-
Semiperimeter (s) = (a+b+c)/2
s = (5 + 6 +7)/2
s = 9
Now Area of a triangle = √[s(s-a)(s-b)(s-c)]
=√[9(9-5)(9-6)(9-7)]
=√ [9 × 4 × 3 × 2]
=√ [3 × 3 × 2 × 2 × 3 × 2]
=√ [32 × 22 × 3 × 2]
= 6√6 square units.
Triangles: Introduction

Frequently Asked Questions – FAQs on Triangles
What are triangles?
How many types of triangles are there in Maths?
Scalene Triangles
Isosceles triangles
Equilateral triangles
Acute triangles
Obtuse triangles
Right triangles
What are the properties of triangles?
Exterior angles of a triangle add up to 360 degrees.
Shortest side is always opposite the smallest angle of a triangle.
What is the perimeter and area of a triangle?
What is the formula for area and perimeter of a triangle?
Area = ½ (Product of base and height of a triangle)
What is scalene, isosceles and equilateral triangle?
If all the three sides are different in length, then its scalene triangle.
If any two sides are equal in length, then it is an isosceles triangle.
If all three sides are equal in length, then it is an equilateral triangle.
What is the difference between acute triangle, obtuse triangle and right triangle?
An obtuse triangle has any one of its angle greater than 90 degrees.
A right triangle has exactly one angle equal to 90 degrees.





Comments