Inelastic Collision Formula

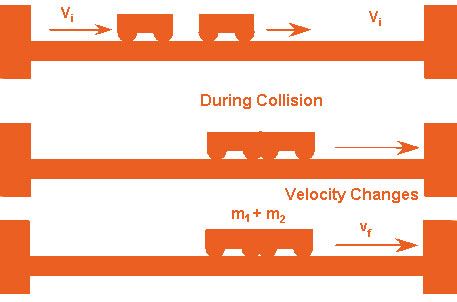
The crash in which kinetic energy of the system is not conserved but the momentum is conserved, then that collision is termed as Inelastic Collision.

Formula of Inelastic Collision

The inelastic collision formula is articulated as

Where
mass of body 1 = m₁

mass of body 2 = m₂
The initial velocity of body 1 = u₁
The initial velocity of body 2 = u₂
The final velocity of both the bodies = v

The final velocity for Inelastic collision is articulated as

The inelastic collision formula is made use of to find the velocity and mass related to the inelastic collision.

Inelastic Collision Solved Example

Problem 1: Compute the final velocity if an object of mass 2 Kg with initial velocity 3 ms^-1 hits another object of mass 3 Kg at rest? (Collision is inelastic)
Answer:
Known:
m₁ (Mass)= 2 Kg,
m₂(Mass) = 3 Kg
u₁ (Initial Velocity of first mass)= 3 ms^-1
u₂ (Initial velocity of second mass) = 0

v = 6/5

v = 1.2 m/s