Complex numbers are algebraic expressions which have real and imaginary parts. If the real part of a complex number is 0, then it is called a “purely imaginary number”. This article gives insight into complex numbers definition and complex numbers solved examples for aspirants so that they can start with their preparation.

Complex Number Definition

A number of the form z = x + iy where x is the real part, y is the imaginary part and x, y belong to a set of real numbers.

\begin{array}{l} The value of i = \sqrt{- 1} . \end{array}

The value of i can’t be seen on the number line.

Representation of a Complex Number

Representation Of A Complex Number

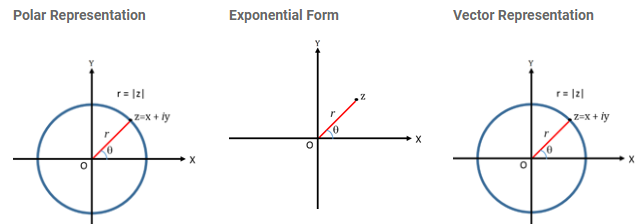
The polar form of z : x = r cos θ, y = r sin θ

The exponential form of z : z = r e^iθ (where e^iθ = cos θ + i sin θ)

Modulus and Argument of a Complex Number

If z = x + iy, then the modulus is denoted by

\begin{array}{l} | z | = \sqrt{a^{2} + b^{2}} . \end{array}

The angle made by the positive direction of the real axis can be defined as the argument of a complex number and denoted by arg(z).

The properties of the modulus of complex numbers are as follows:

\begin{array}{l} 1] | z_{1} z_{2} | = | z_{1} \cdot z_{2} | \\ 2] | z_{1} + z_{2} | \leq | z_{1} + z_{2} | \\ 3] | \frac{z_{1}}{z_{2}} | = \frac{| z_{1} |}{| z_{2} |} \\ 4] | z_{1} - z_{2} | \geq | z_{1} - z_{2} | \end{array}

The identities of arguments are as follows:

\begin{array}{l} 1] A r g (z_{1} z_{2}) \equiv A r g (z_{1}) + A r g (z_{2}) (\mod (- π, π]), \\ 2] A r g (\frac{z_{1}}{z_{2}}) \equiv A r g (z_{1}) - A r g (z_{2}) (\mod (- π, π]) . \\ 3] If z \neq 0 a n d n i s a n y i n t e g e r, t h e n A r g (z^{n}) \equiv n A r g (z) (\mod (- π, π]) . \end{array}

Conjugate of a Complex Number

A number consisting of an equally real and imaginary part which is equal in magnitude but with opposite signs can be termed a complex conjugate of a complex number.

The properties of the conjugate of complex numbers are as follows:

Let z and w be two complex numbers.

\begin{array}{l} 1] \overset{―}{z + w} = \overset{―}{z} + \overset{―}{w} \\ 2] \overset{―}{z - w} = \overset{―}{z} - \overset{―}{w} \\ 3] \overset{―}{z w} = \overset{―}{z} \overset{―}{w} \\ 4] \overset{―}{(\frac{z}{w})} = \frac{\overset{―}{z}}{\overset{―}{w}}, if w \neq 0 \\ 5] \overset{―}{z} = z \Leftrightarrow z \in R \\ 6] \overset{―}{z^{n}} = {(\overset{―}{z})}^{n}, \forall n \in Z \\ 7] | \overset{―}{z} | = | z | \\ 8] {| z |}^{2} = z \overset{―}{z} = \overset{―}{z} z \\ 9] \overset{―}{\overset{―}{z}} = z \\ 10] z^{- 1} = \frac{\overset{―}{z}}{{| z |}^{2}}, \forall z \neq 0 \end{array}

Algebra of Complex Numbers

The different rules for operations on complex numbers are as follows:

\begin{array}{l} 1] z_{1} + z_{2} = (a + b i) + (c + d i) = (a + c) + (b + d) i \\ 2] z_{1} - z_{2} = (a + b i) - (c + d i) = (a - c) + (b - d) i \\ 3] z_{1} z_{2} = (a + b i) (c + d i) = a c + a d i + b c i + b d i^{2} = (a c - b d) + (b c + a d) i \\ 4] \frac{z_{1}}{z_{2}} = \frac{a c + b d}{c^{2} + d^{2}} + \frac{b c - a d}{c^{2} + d^{2}} i . \end{array}

Equality of Complex Numbers

Consider two complex numbers z₁= (a+bi) and z₂= (c + di). They are said to be equal if their real and imaginary parts are equal, that is

\begin{array}{l} z_{1} = z_{2} \to R e (z_{1}) = R e (z_{2}) and I m (z_{1}) = I m (z_{2}) . \end{array}

Complex Numbers

Representation of a Complex Number

Complex Numbers – Top 12 Most Important and Expected JEE Questions

2,780

Complex Number Examples

Solved examples on complex numbers are given below.

Example 1: If z₁, z₂, z₃ are the vertices of an equilateral triangle ABC, such that |z₁− i| = |z₂− i| = |z₃− i|, then what is the value of |z₁+z₂+ z₃|?

Solution:

|z₁− i| = |z₂− i| = |z₃− i|

Hence, z₁, z₂, and z₃ lie on the circle whose centre is i.

Also, the circumcenter coincides.

[z₁+ z₂+ z₃] / 3 = i

⇒ |z₁+ z₂+ z₃| = 3

Example 2: What is the value of λ if the curve y = (λ + 1)x²+ 2 intersects the curve y = λx + 3 at exactly one point?

Solution:

As (λ + 1)x²+ 2 = λx + 3 has only one solution, so D = 0

⇒ λ²− 4(λ + 1)(−1) = 0

Λ²+ 4λ + 4 = 0

Or (λ + 2)²= 0

Therefore, λ = −2

Example 3: If k + ∣k + z²∣ = |z|²;(k ∈ R⁻), what is the possible argument of z?

Solution:

|k + z²| = |z²| − k = |z²| + |k|

⇒ k, z² and 0 + i0 are collinear

⇒ arg (z²)= arg (k)

⇒ 2 arg (z) = π

⇒ arg (z) = π/2

Example 4: Let a≠0 and p(x) be a polynomial of degree greater than 2. If p(x) leaves remainders a and ?a when divided respectively, by x + a and x – a, the remainder when p(x) is divided by x²− a² is?

Solution:

We are given that p(-a) = a and p(a) = -a

(When a polynomial f(x) is divided by x – a, remainder is f[a]),

Let the remainder, when p(x) is divided by x²− a², be Ax+B.

Then,

p(x) = Q(x)(x²− a²) + Ax + B ….. (1)

Where Q(x) is the quotient.

Putting x = a and -a in (1), we get

p(a) = 0 + Aa + B

⇒ −a = Aa + B …. (2)

And p(−a) = 0 − aA + B

⇒ a = −aA + B …….(3)

Solving (2) and (3), we get

B = 0 and A = -1

Hence, the required remainder is -x.

Example 5: If the roots of the equation x²+2ax+b=0 are real and distinct and they differ by at most 2m, then at what interval does b lie?

Solution:

Let the roots be α, β.

∴α + β = −2a and αβ = b

Given, |α − β| ≤ 2m

or |α − β|²≤ (2m)² or(α + β)²− 4ab ≤ 4m² or 4a²− 4b ≤ 4m²

⇒ a²− m²≤ b and discriminant D > 0 or 4a²− 4b > 0

⇒ a²− m²≤ b and b < a².

Hence, b ∈ [a²−m²,a²).

Example 6: Find the conjugate of (2 – i)(1 + 2i)/(2 + 3i)(3 – 2i).

Solution:

We have (2-i)(1+2i)/(2+3i)(3-2i) = (2-i+4i+2)/ (6+9i-4i+6)

= (4+3i) / (12+5i)

Multiply the numerator and denominator by (12-5i).

(4+3i)(12-5i) / (12+5i)(12-5i) = (48+36i-20i+15)/(144+25)

= (63+16i) / 169

Hence, the conjugate is (63+16i) / 169

Example 7: Solve the equation x²+3x+9 = 0

Solution:

We have x²+3x+9 = 0

b²-4ac = 3²-4×1×9 = 9-36 = -27 < 0

∴ x = (-3+√-27)/2 or (-3-√-27)/2 (Using equation [-b±√(b²-4ac)]/2a)

= (-3+√27 i)/2 or (-3-√27 i)/2

Complex Numbers – Important Topics

3,120

Complex Numbers – Important Questions

5,311

Complex Number Definition

Representation of a Complex Number

Modulus and Argument of a Complex Number

Conjugate of a Complex Number

Algebra of Complex Numbers

Equality of Complex Numbers

Related articles

Complex Numbers – Top 12 Most Important and Expected JEE Questions

Complex Number Examples

Complex Numbers – Important Topics

Complex Numbers – Important Questions

Comments

Leave a Comment Cancel reply