The resistivity of alloy manganin is

Nearly independent of temperature

Decreases with increase in temperature

Increases rapidly with increase in temperature

Increases rapidly with decrease in temperature

Electric Current - Definition, Unit, Circuit Conditions

The time rate (t) of the flow of charges (q) through any cross-section is called an electric current. It is a scalar quantity, and its SI unit is ampere (A). If charges ΔQ passes through a cross-section in time Δt, then

Electric Current

\(\begin{array}{l}\mathbf{i_{av}\;=\;\frac{\Delta \;Q}{\Delta \;t}}\end{array} \)

Instantaneous Current Electricity

\(\begin{array}{l}\mathbf{i\;=\;lim_{\Delta t\;\rightarrow \;0}\;\frac{\Delta \;Q}{\Delta \;t}\;=\;\frac{dQ}{dt}}\end{array} \)

If the flow of charge is uniform, then

\(\begin{array}{l}\mathbf{i\;=\;\frac{Q}{t}}\end{array} \)

Note: In a conductor, the electric current is caused by the movement of free electrons. The total number of electrons (- ve charge) and protons (+ ve charge) in a conductor is always the same. Hence, the net charge in a conductor carrying current is zero. Also, the value of the current does not change with the change in the cross-sectional area of the conductor.

Electric current (i) due to the rotatory motion of the charge (q):

If a point charge (q) is moving with speed v in a circular path of radius r, then

\(\begin{array}{l}\mathbf{i\;=q\nu =\;\frac{q}{T}\;=\;\frac{q\; v }{2\;\;\pi \;r}\;=\;\frac{q\;\omega }{2\;\pi }}\end{array} \)

Where,

\(\begin{array}{l}\mathbf{\omega }= \text{angular velocity},\end{array} \)

T = Time period and

\(\begin{array}{l}\nu = \text{frequency}.\end{array} \)

Current electricity when the voltage (V) is applied across the resistance (R):

\(\begin{array}{l}\mathbf{i\;=\;\frac{V}{R}}\end{array} \)

and

\(\begin{array}{l}\mathbf{i\;=\;\frac{P}{V}}\end{array} \)

[Where P = Power]

Note: In solids, the current carriers are the free electrons. In liquids, the current carriers are negative and positive ions. In gases, the current carriers are free electrons and positive ions. In semiconductors, the current carriers are holes and free electrons.

Current Density

The current density in a conductor is the current per unit area of the cross-section of the conductor.

If the area is normal to the direction of the flow of charge, the current density (J) at any point is given by

\(\begin{array}{l}\mathbf{\overrightarrow{J}\;=\;\frac{di}{dA}\;\overrightarrow{n}}\end{array} \)

Or,

\(\begin{array}{l}\mathbf{di\;=\;J\;dA\;cos\; \theta \;=\;\overrightarrow{J}\;.\;\overrightarrow{dA}}\end{array} \)

Therefore, the relationship between current electricity and current density, if the current density is uniform for a normal cross-section,

\(\begin{array}{l}\mathbf{i\;=\int \;\overrightarrow{J}\;.\;\overrightarrow{dA}}\end{array} \)

\(\begin{array}{l}\text{Since},\ \mathbf{\overrightarrow{J}} = \text{Constant}\end{array} \)

Therefore,

\(\begin{array}{l}\mathbf{i\;=\int \;\overrightarrow{J}\;.\;\overrightarrow{dA}\;=\;\overrightarrow{J}\;.\;\int \;\overrightarrow{dA}\;=\;\overrightarrow{J}\;.\;\overrightarrow{A}\;=\;J A\;cos\;0\;=\;J A }\end{array} \)

The dimension of current density is [L^-2 A], and the SI unit is Ampere m^-2.

Different Circuit Conditions

Case 1: When the cell is discharging, i.e., closed circuit

A. The current given by the cell

\(\begin{array}{l}\mathbf{i\;=\;\frac{E}{R\;+\;r} }\end{array} \)

B. The potential difference (PD) across the resistance is given by V = iR

C. Potential drop inside the cell = ir

D. The equation of the cell E = V + ir (E > V)

E. The internal resistance (r) of the cell is given by

\(\begin{array}{l}\mathbf{r\;=\;\left [ \frac{E}{V}\;-\;1 \right ]\;.\;R}\end{array} \)

F. The power (P) dissipated in the external resistance (R) is given by

\(\begin{array}{l}\mathbf{P\;=\;V\;i\;=\;i^{2}\;R\;=\;\frac{V^{2}}{R}\;=\;\left [ \frac{E}{R\;+\;r} \right ]^{2}\;.\;R}\end{array} \)

G. Power = maximum when R = r,

\(\begin{array}{l}i.e., \mathbf{P_{max}\;=\;\frac{E^{2}}{4\;r}}\end{array} \)

Electric Current IIT JEE

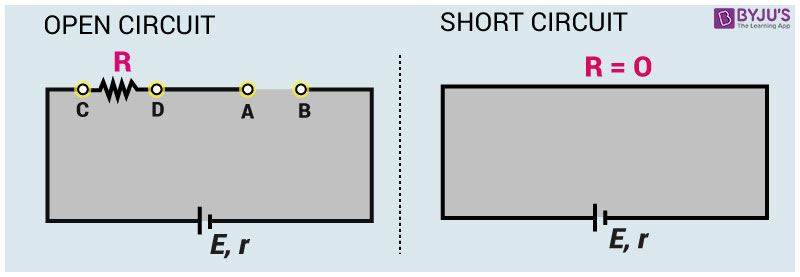
Case 2: Open Circuit Condition

A. Current through the circuit (i) = 0

B. Potential difference between A and B, (V_B) = E

C. Potential difference between C and D, (V_CD) = 0

Case 3: Short Circuit Condition

A. Potential difference (V) = 0

B. Short circuit current = i_sc = E/r

Grouping of Cell

1. If n identical cells are in a series connection.

Electric Current IIT JEE

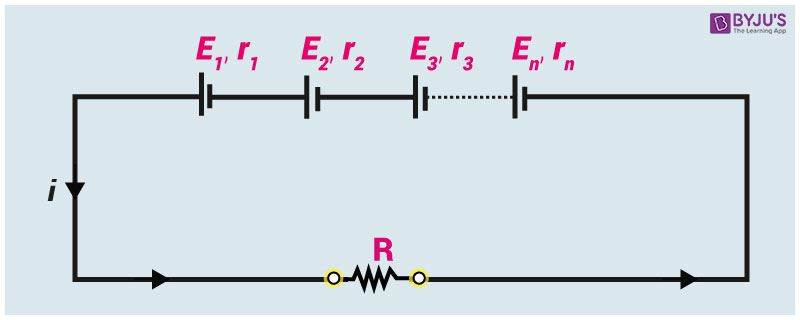
A. The equiv. EMF Eeq = n E

B. The equiv. internal resistance req = n r

C. Electric current from each cell = Main current

\(\begin{array}{l}\mathbf{i\;=\;\frac{n\;E}{R\;+\;nr}}\end{array} \)

D. The potential difference (PD) across external resistance V = i R

E. The potential difference (PD) across each cell

\(\begin{array}{l}\mathbf{V^{‘}\;=\;\frac{V}{n}}\end{array} \)

F. Power (P) dissipated in the circuit

\(\begin{array}{l}\mathbf{P\;=\;\left [ \frac{n\;E}{R\;+\;nr} \right ]^{2}\;.\;R}\end{array} \)

G. For maximum power: R = nr

H. Maximum power

\(\begin{array}{l}\mathbf{P_{max}\;=\;n\;\left [ \frac{E^{2}}{4\;r} \right ]}\end{array} \)

2. If n identical cells are in parallel connection.

Electric Current IIT JEE

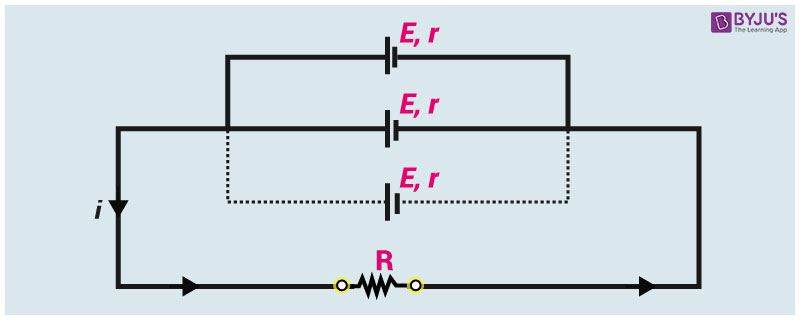
A. The eq. EMF Eeq = E

B. The eq. internal resistance req = r/n

C. Main current

\(\begin{array}{l}\mathbf{i\;=\;\frac{E}{R\;+\;\frac{r}{n}}}\end{array} \)

D. The potential difference (PD) across external resistance = Potential difference across each cell = V = i R

E. Current electricity from each cell = i’ = i/n

F. Power (P) dissipated in the circuit

\(\begin{array}{l}\mathbf{P\;=\;\left [ \frac{E}{R\;+\;\frac{r}{n}} \right ]^{2}\;.\;R}\end{array} \)

G. For maximum power:

\(\begin{array}{l}\mathbf{R\;=\;\frac{r}{n}}\end{array} \)

H. Maximum power

\(\begin{array}{l}\mathbf{P_{max}\;=\;n\;\left [ \frac{E^{2}}{4\;r} \right ]}\end{array} \)

Mixed Grouping: If n number of identical cells are connected in series and m rows are in parallel connection, as shown below.

Electric Current IIT JEE

A. The equiv. EMF Eeq = n E

B. The equiv. internal resistance (req) of the combination req = nr/m

C. Main current through the load

\(\begin{array}{l}\mathbf{i\;=\;\frac{nE}{R\;+\;\frac{nr}{m}}\;=\;\frac{mnE}{mR\;+\;nr}}\end{array} \)

D. Potential difference (PD) across load V = iR

E. Potential difference (PD) across each cell

\(\begin{array}{l}\mathbf{V’\;=\;\frac{V}{n}}\end{array} \)

F. Electric current from each cell

\(\begin{array}{l}\mathbf{i’\;=\;\frac{i}{n}}\end{array} \)

G. For maximum power:

\(\begin{array}{l}\mathbf{R\;=\;\frac{nr}{m}}\end{array} \)

H. Maximum power

\(\begin{array}{l}\mathbf{P_{max}\;=\;mn\left [ \frac{E^{2}}{4r} \right ]}\end{array} \)

I. The total number of cells = m × n

Electric Current IIT JEE Study Material

Different Circuit Conditions

Grouping of Cell

Video Lessons

Current Electricity – JEE Main Important Topics

Current Electricity – JEE Solved Questions

Current Electricity Important JEE Main Questions

Current Electricity – Important and Previous Year Questions

Capacitors and Electric Current – JEE Advanced PYQs

Current Electricity – JEE Main Important and Expected Questions

Comments

Leave a Comment Cancel reply

FREE TEXTBOOK SOLUTIONS