Having a good knowledge of vector operations is important as in physics we have to deal with numerous vector quantities. Some of the FAQ’s related to these topics are discussed below.
Important Questions For Vector Operations
- What is meant by equality of vectors?
Ans – Two vectors are said to be equal if their magnitudes and directions are the same. Here we are talking about two values of the same physical quantity, i.e. we can not talk about equality of two vectors if they don’t represent the same physical quantity. For instance, one can’t say that the velocity vector of 5 m/s in the positive x-axis and Force vector of 5 N also in the positive x-axis is equal.
- Explain the addition and subtraction of vectors.
Ans –
Addition of vectors:
The addition of vectors is done based on Triangle Rule:
Suppose there are two vectors:
\(\begin{array}{l}\vec{a}\ \text{and}\ \vec{b}\end{array} \)
\(\begin{array}{l}\text{Now, draw a line AB representing}\ \vec{a}\ \text{with A as the tail and B as the head.}\end{array} \)
\(\begin{array}{l}\text{Draw another line BC representing}\ \vec{b}\ \text{with B as the tail and C as the head.}\end{array} \)
Now join the line AC with A as the tail and C as the head. \(\begin{array}{l}\text{The line AC represents the resultant sum of the vectors}\ \vec{a}\ \text{and}\ \vec{b}\end{array} \)
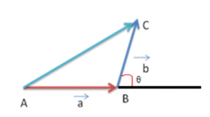
The line AC represents
\(\begin{array}{l}\vec{a}+\vec{b}\end{array} \)
\(\begin{array}{l}\text{The magnitude of }\ \vec{a}+\vec{b}=\sqrt{a^2\;+\;b^2\;+\;2ab\;cos\; \theta}\end{array} \)
Where,
\(\begin{array}{l}a = \text{magnitude of vector}\ \vec{a}\end{array} \)
\(\begin{array}{l}b = \text{magnitude of vector}\ \vec{b}\end{array} \)
\(\begin{array}{l}\theta = \text{angle between}\ \vec{a}\ \text{and}\ \vec{b}\end{array} \)
Let the resultant vector make an angle of θ with
\(\begin{array}{l}\vec{a},\ \text{then}\ tan\ \theta = \frac{b\;sin\;\theta}{a+b\;cos\; \theta}\end{array} \)
Let us understand this by the means of an example. Suppose there are two vectors having equal magnitude A, and they make an angle θ with each other. Now, to find the magnitude and direction of the resultant vector, we will use the formulas mentioned above.
Let the magnitude of the resultant vector be B
\(\begin{array}{l}B = \sqrt{A^2\;+\;A^2\;+\;2AA\;cos\; \theta}\end{array} \)
\(\begin{array}{l}=2A\;cos \; \frac{ \theta}{2}\end{array} \)
Let’s say that the resultant vector makes an angle θ with the first vector
\(\begin{array}{l}tan\ \theta = \frac{A\;sin\; \theta}{A\;+\;A\;cos\; \theta}\end{array} \)
\(\begin{array}{l}=tan\;\frac{ \theta}{2}\end{array} \)
Or,
θ = θ/2
Subtraction of vectors:
The subtraction of two vectors is similar to the addition of vectors.
\(\begin{array}{l}\text{Suppose}\ \vec{a}\ \text{is to be subtracted from}\ \vec{b}.\end{array} \)
\(\begin{array}{l}\vec{a} – \vec{b}\ \text{can be said as the addition of the vectors}\ \vec{a}\ \text{and}\ (-\vec{b}).\end{array} \)
Thus, the formula for addition can be applied as:
\(\begin{array}{l}\vec{a}-\vec{b} = \sqrt{a^2\;+\;b^2\;-\;2ab\;cos \theta}\end{array} \)
\(\begin{array}{l}(-\vec{b})\ \text{is nothing but}\ \vec{b}\ \text{reversed in direction}.\end{array} \)
- Explain the multiplication of a vector by a scalar.
Ans. –
\(\begin{array}{l}\text{Suppose}\ \vec{a}\ \text{is a vector of magnitude ‘a’ and n is a number}.\end{array} \)
\(\begin{array}{l}\text{If we multiply}\ \overrightarrow{a}\ \text{by n, then we will get a new vector}.\end{array} \)
\(\begin{array}{l}\text{Let’s say this vector is}\ \vec{b}.\end{array} \)
We define vector
\(\begin{array}{l}\vec{b} = n\vec{a}\end{array} \)
as the vector of magnitude na. \(\begin{array}{l}\text{The direction of the vector}\ \vec{b}\ \text{will be the same as of vector}\ \vec{a},\end{array} \)
\(\begin{array}{l}\text{i.e. if the vector}\ \vec{a}\ \text{is in positive x direction,}\end{array} \)
\(\begin{array}{l}\vec{b}\ \text{will be in positive x direction; if the vector}\ \vec{a}\ \text{is in negative x direction,}\end{array} \)
\(\begin{array}{l}\vec{b}\ \text{will be in negative x direction.}\end{array} \)
If this number n is negative, the direction of
\(\begin{array}{l}\vec{b}\ \text{is opposite to the direction of the vector}\ \vec{a}.\end{array} \)
If n= -1, then multiplication by n just reverses the direction of the vector.
- What are some of the best books to refer for vector operations in physics?
Ans – Knowledge of vector is very important as it forms the backbone for physics. Halliday and Resnick are good books to learn the concepts while students can also refer to H.C. Verma or Arihant publication for problem-solving.
To know more about different topics in physics keep visiting BYJU’S.

Comments