Graphical Representation of Simple Harmonic Motion

Simple harmonic motion (SHM) is a repetitive back and forth motion about an equilibrium position. The time period of each complete vibration will be the same. The SHM is characterised by the changing acceleration that is directly proportional to the equilibrium position, and it is always directed towards the equilibrium position.

Characteristics of Simple Harmonic Motion

Displacement: It is the distance of the particle from the mean or equilibrium position. It is denoted as ‘y’ if the SHM is along the y-axis, and it is denoted as ‘x’ if the SHM is along the x-axis.

Amplitude: The maximum displacement of the particle on either side of the mean position is called the amplitude.

Oscillation: One complete two and fro motion about the mean position is called an oscillation.

Time Period: The time required for one complete oscillation is called the time period.

Frequency: The number of oscillations completed in one second by the particle is called frequency.

Phase: Phase signifies the state of motion of the particle.

Velocity and Acceleration of the Particle Executing Simple Harmonic Motion

Let us consider a particle that executes SHM along the y-axis. The equation of motion of the particle is given by the expression

y = A sin ωt

Here, A is the amplitude

ω is the angular frequency

The velocity of the particle executing simple harmonic motion along the y-axis

v = dy/dt = Aω cos (ωt)

v² = (Aω)² cos ²(ωt)

= ω² [A² – A²sin²ωt]

= ω² [A² – y²] (since y = A sin ωt)

v = √ω² [A² – y²]

Put y = 0, v = Aω

Put y = A, v = 0

Therefore, the velocity of the particle executing simple harmonic motion is maximum at the equilibrium position and minimum at the extreme position.

The equation of velocity can also be written as

v² = ω² [A² – y²]

v² + ω²y²= ω²A²

(v²/ω²A²)+ (y²/A²) = 1 (standard equation of ellipse)

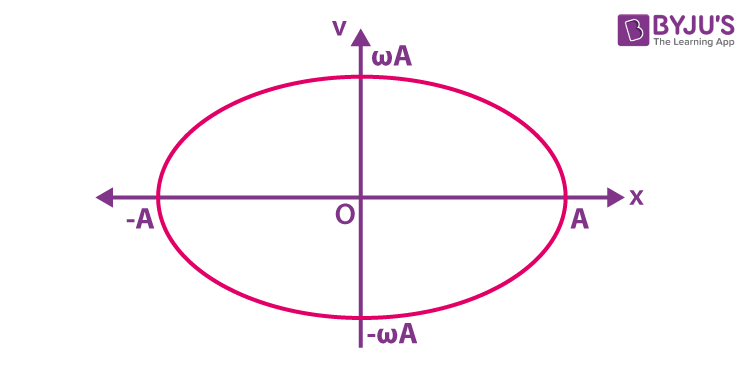
This is a standard equation of an ellipse. The graph between velocity and displacement is an ellipse, and it can be represented as follows:

The acceleration of the particle is given by the equation,

a = – Aω²sin(ωt)

a = – ω²y

This shows that acceleration is proportional to the displacement, and it is in opposite directions.

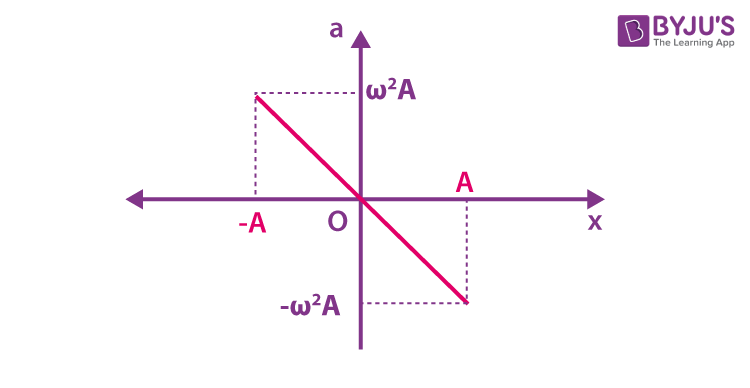
The graph of acceleration vs displacement is a straight line with a negative slope.

Graphical Representation of Simple Harmonic Motion

The graphical representation of displacement, velocity and acceleration of the particle vibrating in SHM is given below.

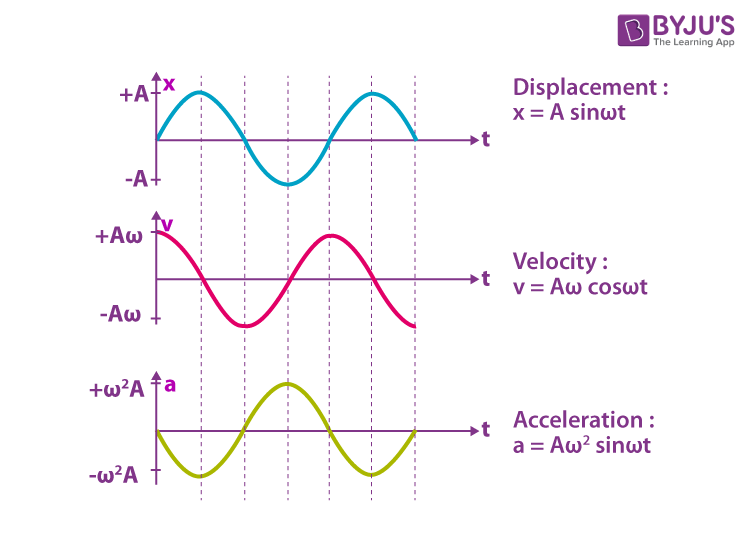
(i) The displacement of the particle is given by the expression y = A sin ωt. When y = ± A, the displacement of the particle is maximum.

The equation of velocity can also be written as y = A sin (ωt + 0) ——-(1)

(ii) The velocity of the particle executing SHM is given by v = Aω cos (ωt). The velocity of the particle is maximum at the mean position, i.e., v = ± Aω, and at the extreme position, it will be zero.

The equation of velocity can also be written as v =Aω sin (ωt + π/2) ——–(2)

(iii) The acceleration of the particle executing simple harmonic motion is a = – Aω²sin(ωt). The acceleration will be maximum at the extreme position, and it is zero at the mean position.

The equation of acceleration can also be written as a = Aω² sin (ωt + π) ——–(3)

From the equations (1), (2) and (3), we can understand that the phase difference between displacement, velocity and acceleration is π/2.

Solved Questions

1. Which of the following options gives the phase difference between displacement and velocity in simple harmonic motion?

a) zero

b) π

c) π/2

d) 3π/4

Answer: c) π/2

2. Which of the following statements is true regarding the acceleration of the particle executing simple harmonic motion?

(a) Acceleration is zero at the mean position

(b) Acceleration is maximum at the mean position

(c) Acceleration is zero at the extreme position

(d) It is a constant

Answer: (a) Acceleration is zero at the mean position

Video Lessons

Simple Harmonic Motion (SHM) – JEE Concept

Angular SHM (Simple Harmonic Motion)

What Is Energy in SHM?

Graphical Representation of SHM