Important Centre of Mass Formulas for JEE Main and Advanced

Before we look at the centre of mass formulas lets us quickly look at what the concept means. The centre of mass of a body is defined as a point at which whole of the mass of the body appears to be concentrated. The centre of mass of few useful configurations is given below.

Centre of Mass Formulas

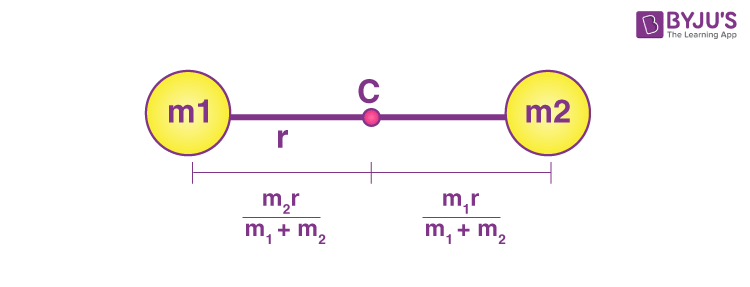
1. A system of two point masses m₁r₁ = m₂r_2. The centre of mass lies closer to the heavier mass.

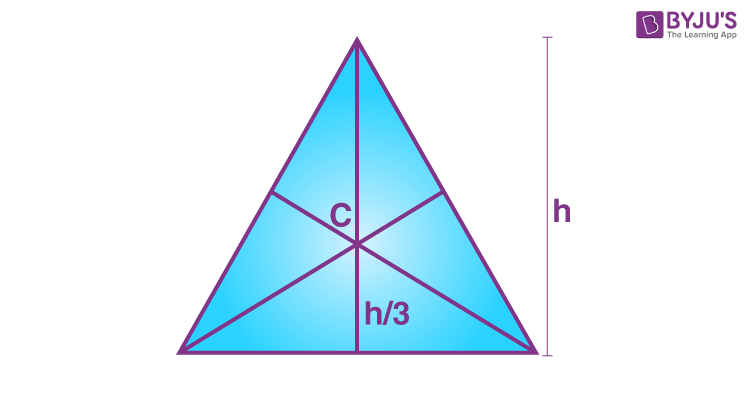
2. Triangle (at the centroid)

y_c=h/3

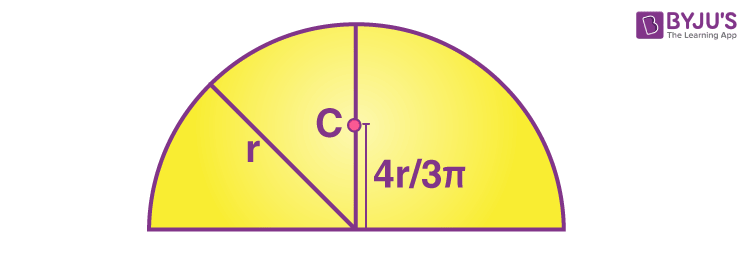
3. A semi-circular disc

y_c= 4r/3π

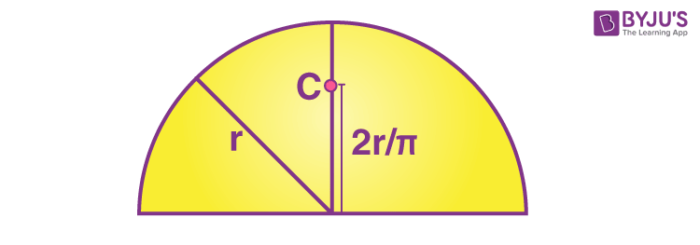
4. Semicircular ring

y_c= 2r/π

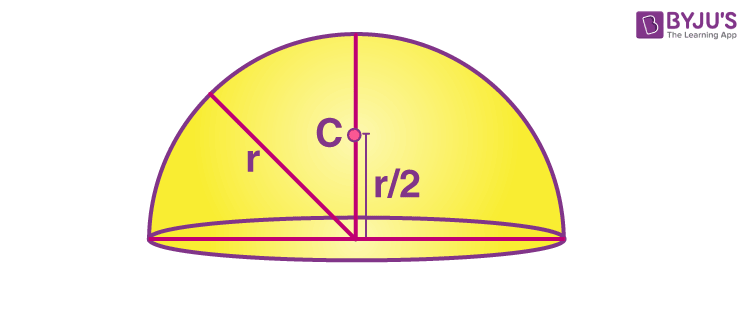
5. Hemispherical shell

y_c= r/2

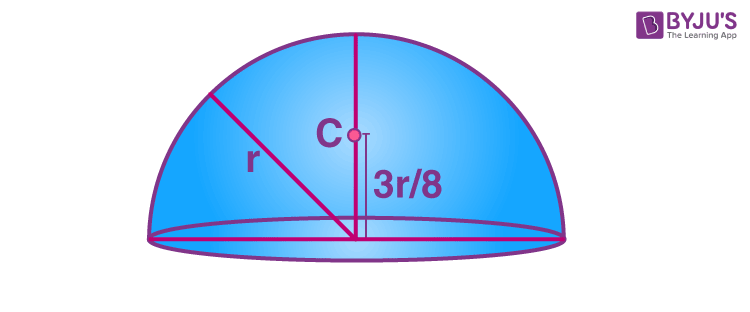
6. Solid Hemisphere

y_c =3r/8

7. Cone.

The height of the centre of mass from the base is h/4 for the solid cone and h/3 for the hollow cone.

Centre of Mass Videos

Problem illustration on Centre of Mass

Motion of the Centre of Mass and Conservation of Momentum

1. Velocity of centre of mass

\(\begin{array}{l}\vec{V}_{cm}=\frac{m_{1}\vec{v_{1}}+m_{2}\vec{v_{2}}——-m_{n}\vec{v_{n}}}{M}\end{array} \)

\(\begin{array}{l}\vec{p}_{cm}=M\vec{v_{cm}}\end{array} \)

2. Acceleration of centre of mass

\(\begin{array}{l}\vec{a}_{cm}=\frac{m_{1}\vec{a_{1}}+m_{2}\vec{a_{2}}——-m_{n}\vec{a_{n}}}{M}\end{array} \)

\(\begin{array}{l}\vec{a}_{cm}=\vec{F}_{ext}{M}\end{array} \)

Impulse

\(\begin{array}{l}\vec{J}=\int \vec{F}{dt}=\Delta\vec{p}\end{array} \)

Collision

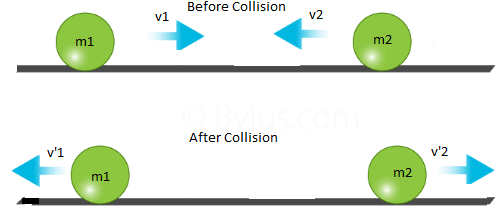
Momentum conservation m₁v₁+m₂v₂ =m₁v’₁ + m₂v’₂

Elastic Collision= ½ m₁v₁² + ½ m₂v₂² = ½ m₁v’₁ ²+½m₂v’₂²

Coefficient of restitution

\(\begin{array}{l}e=\frac{-(v’_{1}-v’_{2})}{v_{1}-v_{2}}\end{array} \)

e=0, completely elestic collision

e=1, completely inelastic collision

If v₂=0 and m₁≪ m₂ then v’₁ = -v₁

If v₂=0 and m₁ ≫ m₂ then v’₂ = 2v₁

Elastic Collision with m1=m2 then v’₁ = v₂ and v’₂ = v₁