Increasing and Decreasing Functions in Calculus

In calculus, the derivative of a function is used to check whether the function is decreasing or increasing at any interval in a given domain. For a given function, y = F(x), if the value of y increases on increasing the value of x, then the function is known as an increasing function, and if the value of y decreases on increasing the value of x, then the function is known as a decreasing function.

In both of the given functions, x₁ < x₂ and F(x₁) < F(x₂), we can say it is an increasing function.

F(x) = e^-x

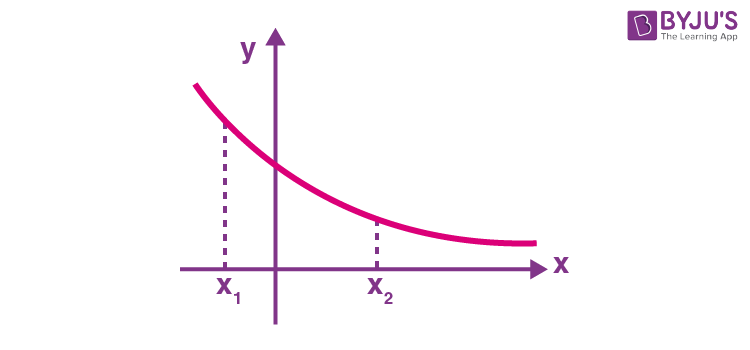
In this function, value of y decreases on increasing the value of x as x₁ < x₂ and F(x₁) < F(x₂).

Increasing Function in Calculus

For a function, y = f(x) to be increasing (dy/dx) ≥ 0 for all such values of interval (a, b), and equality may hold for discrete values.

Example: Check whether y = x³ is an increasing or decreasing function.

Solution:

So, it is an increasing function.

Graphical Representation:

Decreasing Function in Calculus

For a function, y = f(x) to be monotonically decreasing (dy/dx) ≤ 0 for all such values of interval (a, b), and equality may hold for discrete values.

Example: Check whether the function y = -3x/4 + 7 is an increasing or decreasing function.

Differentiate the function with respect to x, and we get

So, we can say it is a decreasing function.

Solved Questions on Increasing and Decreasing Functions

Question 1: Prove that f(x) = x – sin(x) is an increasing function.

Solution: f(x) = x – sin(x)

(dy/dx) ≥ 0 as cos(x) having a value in the interval [-1, 1] and (dy/dx) = 0 for the discrete values of x and do not form an interval.

Hence, we can include this function as a monotonically increasing function.

Question 2: Prove that f(x) = cos x is decreasing function in [0, π].

Solution: f(x) = cos x

f’(x) = – sin x

As sin x is positive in the first and second quadrants, i.e., sin x ≥ 0 in [0, π], so we can say that

(dy/dx) = – (positive ) = negative ≤ 0

So, function f(x) = cos x is decreasing in [0, π].

Question 3: Prove that a polynomial with positive coefficients is increasing.

Solution: Let’s suppose polynomial is

So,

Derivate the above function with respect to x, and we have

As every coefficient is positive, and for a polynomial n ≥ 0.

So,

Therefore, we can say that a polynomial with positive coefficients is increasing.

Question 4: Discuss the increasing and decreasing nature of the function f(x) = x ln(x)

Solution:

Here, f(x) = x ln(x)

⇒ f’(x) = 1 + ln(x)

For a function to be increasing f’(x) > 0

⇒ 1 + ln(x) > 0

⇒ ln(x) > -1

⇒ ln(x) > – ln(e)

⇒ ln(x) > ln (e^-1)

We know that ln(x) is increasing function, so for ln(x) > ln (e^-1) to be hold

⇒ x > e^-1

⇒ x > 1/e

Thus, function f(x) = x ln(x) to be increasing x ∈ (1/e, ∞) and for function f(x) = x ln(x) to be decreasing x ∈ (0, 1/e).

Question 5: Find the value of “a” if the function x³ – 6x² + ax is increasing for all the values of x.

Solution:

Here f(x) = x³ – 6x² + ax

⇒ f’(x) = 3x² – 12x + a

For a function to be increasing f’(x) > 0

So, 3x² – 12x + a > 0

⇒ 3(x² – 4x + a/3) > 0

⇒ x² – 4x + a/3 > 0

⇒ (x – 2)² – 2² + a/3 > 0

⇒ (3(x – 2)² – 12 + a)/3 > 0

⇒ 3(x – 2)² – 12 + a > 0

We know that 3(x – 2)² can’t be negative and having the minimum value 0 at x = 2

The minimum value of f’(x) is at x = 2

min. f’(x) = -12 + a

So for f’(x) > 0

⇒ -12 + a > 0

⇒ a > 12.

Video Lessons

Domain, Range, Period of Functions

Functions and Relations

Increasing and Decreasing Functions

Increasing and Decreasing Functions in One-Shot for JEE Mains 2023