Integration is the process of finding the antiderivative. The integration of g′(x), with respect to dx, is given by
∫ g′(x) dx = g(x) + C, where C is the constant of integration.
The two types of integrals are
- Definite integral: An integral with limits, namely upper and lower limits, without the constant of integration.
- Indefinite integral: An integral without limits and with an arbitrary constant.
This article covers standard integrals, properties of integration, important formulas and examples of integration which helps students to have a deep knowledge of the topic.
Standard Integrals
Integrals of Rational and Irrational Functions
\(\begin{array}{l}\int x^n dx = \frac{x^{n+1}}{n+1} + C , n \ne 1\\ \int \frac{1}{x} dx = \ln|x| + C \\ \int c \, dx = c \cdot x + C \\ \int x \, dx = \frac{x^2}{2} + C \\ \int x^2 \, dx = \frac{x^3}{3} + C \\ \int \frac{1}{x^2} dx = -\frac{1}{x} + C \\\end{array} \)
\(\begin{array}{l}\int \sqrt{x} \, dx = \frac{2\cdot x \cdot \sqrt{x} }{3} + C\\ \int \frac{1}{1+x^2} dx = \arctan x + C \\ \int \frac{1}{\sqrt{1-x^2}} dx = \arcsin x + C \\\end{array} \)
Integrals of Trigonometric Functions
\(\begin{array}{l}\int \sin x\,dx = -\cos x + C \\ \int \cos x\,dx = \sin x + C\\ \int \tan x\,dx = \ln|\sec x| + C \\ \int \sec x\,dx = \ln|\tan x + \sec x | + C \\\end{array} \)
\(\begin{array}{l}\int \sin^2x\,dx = \frac{1}{2}(x-\sin x \cdot \cos x) + C\\ \int \cos^2x\,dx = \frac{1}{2}(x + \sin x \cdot \cos x) + C \\ \int \tan^2x\,dx = \tan x – x + C \\ \int \sec^2x\,dx = \tan x + C \\\end{array} \)
Integrals of Exponential and Logarithmic Functions
\(\begin{array}{l}\int \ln x \,dx =x \cdot \ln x -x + C \\ \int x^n \cdot \ln x \,dx =\frac{x^{n+1}}{n+1} \ln x – \frac{x^{n+1}}{(n+1)^2} + C \\ \int e^x\,dx = e^x + C \\ \int a^x\,dx = \frac{a^x}{\ln a} + C\\\end{array} \)
Properties of Integration
Property 1:
\(\begin{array}{l}\int\limits_{a}^{a}{f(x)\,dx=0}\end{array} \)
Property 2:
\(\begin{array}{l}\int\limits_{a}^{b}{f(x)dx=}-\int\limits_{b}^{a}{f(x)dx}\end{array} \)
Property 3:
\(\begin{array}{l}\int\limits_{a}^{b}{f(x)dx=}\int\limits_{a}^{b}{f(t)dt}\end{array} \)
Property 4:
\(\begin{array}{l}\int\limits_{a}^{b}{f(x)dx=}\int\limits_{a}^{c}{f(x)dx+\int\limits_{a}^{b}{f(x)dx}}\end{array} \)
Property 5:
\(\begin{array}{l}(i)\ \int\limits_{a}^{b}{f(x)dx=}\int\limits_{a}^{b}{f(a+b-x)dx}\end{array} \)
\(\begin{array}{l}(ii)\ \int\limits_{0}^{a}{f(x)dx=}\int\limits_{0}^{a}{f(a-x)dx}\end{array} \)
⇒ Also Read: Definite and Indefinite Integration
Useful Formulas
- \(\begin{array}{l}\int{{{e}^{ax}}\sin bx=\frac{{{e}^{ax}}}{{{a}^{2}}+{{b}^{2}}}\left[ a\sin bx-b\cos bx \right]}\end{array} \)
- \(\begin{array}{l}\int{{{e}^{ax}}\cos bx=\frac{{{e}^{ax}}}{{{a}^{2}}+{{b}^{2}}}\left[ a\cos bx+b\sin bx \right]}\end{array} \)
- \(\begin{array}{l}\int{{{e}^{x}}\left( f(x)+f'(x) \right)}={{e}^{x}}f(x)\end{array} \)
Illustration:
\(\begin{array}{l}\int{{{e}^{x}}(\sin x+\cos x)dx={{e}^{x}}\sin x+c\\}\end{array} \)
\(\begin{array}{l}\int{{{e}^{x}}(lnx+\frac{1}{x})dx={{e}^{x}}lnx+c}\end{array} \)
Integration of Trigonometric Functions
Type 1:
\(\begin{array}{l}I=\int{{{\sin }^{m}}x{{\cos }^{n}}xdx}\end{array} \)
1. If m is odd, put cos x = t
2. If n is odd, put sin x = t
3. If m, n rationales then put tan x = t
4. If both are even, then use the reduction method.
\(\begin{array}{l}Q\int{\frac{{{\cos }^{3}}x}{{{\sin }^{6}}x}dx=\int{\frac{1-{{t}^{2}}}{{{t}^{6}}}dt}}\end{array} \)
Where t = sin x
\(\begin{array}{l}=\int{{{t}^{-6}}-{{t}^{-4}}dt}\end{array} \)
\(\begin{array}{l}=-\frac{1}{5si{{n}^{5}}x}+\frac{1}{3{{\sin }^{3}}x}+c\end{array} \)
Type 2:
\(\begin{array}{l}\int{\frac{dx}{a\cos x+b\sin x+c}}\end{array} \)
Put t = tan (x/2)
Illustration
\(\begin{array}{l}\int{\frac{dx}{2+\sin x}}\end{array} \)
\(\begin{array}{l}\Rightarrow t=\tan \left( \frac{x}{2} \right)\end{array} \)
\(\begin{array}{l}dx=\frac{2dt}{1+{{t}^{2}}}\end{array} \)
\(\begin{array}{l}=\int{\frac{\frac{2dt}{1+{{t}^{2}}}}{2+\frac{2t}{1+{{t}^{2}}}}}\end{array} \)
\(\begin{array}{l}\Rightarrow \int{\frac{dt}{{{t}^{2}}+t+1}}\end{array} \)
\(\begin{array}{l}=\frac{2}{\sqrt{3}}{{\tan }^{-1}}\left( \frac{2t+1}{\sqrt{3}} \right)\end{array} \)
\(\begin{array}{l}=\frac{2}{\sqrt{3}}{{\tan }^{-1}}\left( \frac{2\tan \frac{x}{2}+1}{\sqrt{3}} \right)+c\end{array} \)
Some Useful Substitutions for Irrational Functions
- Form 1 : \(\begin{array}{l}\int{linear\sqrt{Quadratic}\,dx}\end{array} \)
\(\begin{array}{l}\text{Substitute}\ linear=mQudratic’+n\end{array} \)
- Form 2: \(\begin{array}{l}\int{\frac{dx}{lin\sqrt{li{{n}_{1}}}},}\,\int{\frac{lin}{\sqrt{li{{n}_{1}}}}}dx,\,\int{\frac{\sqrt{li{{n}_{1}}}}{lin}dx}\end{array} \)
\(\begin{array}{l}\text{Substitute}\ li{{n}_{1}}={{t}^{2}}\end{array} \)
- Form 3: \(\begin{array}{l}\int{\frac{1}{lin\sqrt{Qua}}dx}\end{array} \)
Substitute lin = 1/t
- Form 4: \(\begin{array}{l}\int{\frac{dx}{\left( a{{x}^{2}}+b \right)\sqrt{\left( {{x}^{2}}+d \right)}}}\end{array} \)
Substitute x = 1/t and then u2 for at2 + b
Integration Formulas
- \(\begin{array}{l}\int\limits_{a}^{b}{f(x)dx=}\int\limits_{a}^{b}{f(t)dt}\end{array} \)
- \(\begin{array}{l}\int\limits_{a}^{b}{f(x)dx=}-\int\limits_{b}^{a}{f(x)dx}\end{array} \)
- \(\begin{array}{l}\int\limits_{a}^{b}{f(x)dx=}\int\limits_{a}^{c}{f(x)dx}+\int\limits_{c}^{b}{f(x)dx}\end{array} \)
- \(\begin{array}{l}\int\limits_{a}^{b}{f(x)dx=}\int\limits_{a}^{b}{f(a+b-x)dx}\end{array} \)
- \(\begin{array}{l}\int\limits_{0}^{2a}{f(x)dx}=\int\limits_{0}^{a}{f(x)dx}+\int\limits_{0}^{a}{f(2a-x)dx}\end{array} \)\(\begin{array}{l}=0\ \text{if}\\,f(2a-x)=-f(x)\end{array} \)and\(\begin{array}{l}=2\int\limits_{0}^{a}{f(x)}\ \text{if}\ \,f(2a-x)=f(x)\end{array} \)
- \(\begin{array}{l}\int\limits_{-a}^{a}{f(x)dx=\left\{ \begin{matrix} 0 & if\,\,f\left( x \right)\ \text{is odd} \\ 2\int\limits_{0}^{a}{f\left( x \right)dx} & if\,\,f\left( x \right)\ \text{is even} \\ \end{matrix} \right.\,\,\,\,\,\,}\end{array} \)
Problems on Integration
Illustration:
\(\begin{array}{l}\int\limits_{0}^{2}{{{x}^{2}}\left[ x \right]dx=}\int\limits_{0}^{1}{{{x}^{2}}\left[ x \right]dx}+\int\limits_{1}^{2}{{{x}^{2}}\left[ x \right]dx}\end{array} \)
\(\begin{array}{l}=\int\limits_{0}^{1}{{{x}^{2}}.0\,dx}+\int\limits_{1}^{2}{{{x}^{2}}\left[ 1 \right]dx}\end{array} \)
\(\begin{array}{l}=0+\left. \frac{{{x}^{3}}}{3} \right|_{1}^{2}\end{array} \)
\(\begin{array}{l}=\frac{8-1}{3}\,=\frac{7}{3}\end{array} \)
Illustration:
\(\begin{array}{l}\int\limits_{{\pi }/{6}\;}^{{\pi }/{3}\;}{\frac{\sqrt{\sin x}}{\sqrt{\sin x}+\sqrt{\cos x}}dx}\end{array} \)
\(\begin{array}{l}I = \int{\frac{\sqrt{\cos x}}{\sqrt{\sin x}+\sqrt{\cos x}}dx}\ \(\text{by}\ x\to \frac{\pi}{2} – x)\end{array} \)
\(\begin{array}{l}2I=\int\limits_{{\pi }/{6}\;}^{{\pi }/{3}\;}{\frac{\sqrt{\sin x}+\sqrt{\cos x}}{\sqrt{\sin x}+\sqrt{\cos x}}}=\int\limits_{{\pi }/{6}\;}^{{\pi }/{3}\;}{1\,dx}=\frac{\pi }{6}\end{array} \)
\(\begin{array}{l}I=\frac{\pi }{12}\end{array} \)
Illustration:
\(\begin{array}{l}I=\int{{{\sin }^{100}}x{{\cos }^{99}}x}\end{array} \)
Here, f(2π – x) = f(x)
Or
\(\begin{array}{l}I=2\int\limits_{0}^{\pi }{{{\sin }^{100}}x{{\cos }^{99}}x}\end{array} \)
\(\begin{array}{l}=2\int\limits_{0}^{\pi }{{{\sin }^{100}}\left( \pi -x \right){{\cos }^{99}}\left( \pi -x \right)}\end{array} \)
I = -I
I = 0
Illustration:
\(\begin{array}{l}\int\limits_{-5}^{5}{{{x}^{3}}=0}\ \text{as}\ f(x)\ \text{is odd}\end{array} \)
Leibnitz’s rule
\(\begin{array}{l}\frac{d}{dx}\int\limits_{u\left( x \right)}^{v\left( x \right)}{f\left( t \right)dt=f\left( v\left( x \right) \right)}\frac{dv\left( x \right)}{dx}-f\left( u\left( x \right) \right)u’\left( x \right)\end{array} \)
Practice Problems
Problem 1.
\(\begin{array}{l}\text{If}\ \int\limits_{{{x}^{2}}}^{{{x}^{3}}}{\frac{1}{\log t}dt=y}\ \text{find}\end{array} \)
\(\begin{array}{l}\frac{dy}{dx}=x\left( x-1 \right){{\left( \log x \right)}^{-1}}\end{array} \)
Problem 2.
\(\begin{array}{l}\text{If}\ \int\limits_{\sin x}^{1}{{{t}^{2}}f\left( t \right)dt=1-\sin x.}\end{array} \)
where x ∈ (0, π/2), find f(1/√3).
Problem 3.
\(\begin{array}{l}\text{If}\ f\left( 2 \right)=6,f’\left( 2 \right)=\frac{1}{48}.\ \text{Find}\underset{x\to 2}{\mathop{\lim }}\,\int\limits_{6}^{f\left( x \right)}{\frac{4{{t}^{3}}}{x-2}}dt=18.\end{array} \)
Problem 4.
\(\begin{array}{l}\underset{x\to \infty }{\mathop{\lim }}\,\frac{\int\limits_{0}^{x}{{{e}^{{{x}^{2}}}}dx}}{\int\limits_{0}^{x}{{{e}^{2{{x}^{2}}}}dx}}=0\end{array} \)
Integration by Parts
\(\begin{array}{l}\int{uv\,dx}=u\int{vdx}-\int{u’\left( \int{vdx} \right)}\,dx\end{array} \)
Illustration:
Q.
\(\begin{array}{l}\int{\ell n\,x}=\int{\ell n\,\,x.1\,\,dx}\end{array} \)
\(\begin{array}{l}=x\,\ell n\,x-\int{\frac{1}{x}.\,x}\,dx\end{array} \)
\(\begin{array}{l}=x\,\ell n\,x-x\end{array} \)
Q.
\(\begin{array}{l}\int{x\,{{e}^{x}}dx=x\int{{{e}^{x}}dx-\int{{{\left( 1 \right)}}\left( \int{{{e}^{x}}dx} \right)}dx}}\end{array} \)
\(\begin{array}{l}=x{{e}^{x}}-\int{{{e}^{x}}dx}\end{array} \)
\(\begin{array}{l}=x{{e}^{x}}-{{e}^{x}}\end{array} \)
Integration of Irrational Algebraic Functions
Type
\(\begin{array}{l}\int{\frac{dx}{{{\left( ax+b \right)}^{k}}\sqrt{px+q}}}\end{array} \)
Q.
\(\begin{array}{l}\int{\frac{x}{\left( x-3 \right)\sqrt{x+1}}dx}\end{array} \)
Put x + 1 = t2, we get
\(\begin{array}{l}I=\int{\frac{\left( {{t}^{2}}-1 \right)2t\,dt}{\left( {{t}^{2}}-4 \right)t}}=2\int{\frac{{{t}^{2}}-1}{{{t}^{2}}-4}dt}\end{array} \)
\(\begin{array}{l}=2\int{1}+\frac{3}{{{t}^{2}}-4}dt\end{array} \)
\(\begin{array}{l}=2t+\frac{3}{2}\ell n\left| \frac{t-2}{t+2} \right|+c\end{array} \)
\(\begin{array}{l}=2\sqrt{x+1}+\frac{3}{2}\ell n\left| \frac{\sqrt{x+1}-2}{\sqrt{x+1}+2} \right|+c\end{array} \)
\(\begin{array}{l}\Rightarrow \int\limits_{0}^{2a}{f\left( x \right)dx=\int\limits_{0}^{a}{f\left( x \right)dx+}}\int\limits_{0}^{a}{f\left( 2a-x \right)dx}\end{array} \)
= 0 if f(2a – x) = -f(x)
\(\begin{array}{l}=2\int\limits_{0}^{a}{f\left( x \right)}\ \text{if}\ f(2a – x) = f(x)\end{array} \)
Optimisation of Area for Greatest and Least Values
Illustration:
If area by y = f(x) and y = x2 + 2 between abscissa x = 2 and x = α is α3 – 4α2 + 8. Find f(x).
Answer:
\(\begin{array}{l}{{\alpha }^{3}}-4{{\alpha }^{2}}+8=\int\limits_{2}^{\alpha }{\left( {{x}^{2}}+2-f\left( x \right) \right)dx}\end{array} \)
Differentiating with Labniz equation,
\(\begin{array}{l}3{{\alpha }^{2}}-8\alpha ={{\alpha }^{2}}+2-f\left( \alpha \right)\end{array} \)
\(\begin{array}{l}f\left( x \right)=-2{{x}^{2}}+8x+2\end{array} \)
Integrations Important JEE Main Questions
Definite Integration JEE Questions
Indefinite Integration JEE Questions
Solved Problems on Integration
Problem 1:
\(\begin{array}{l}\int_{{}}^{{}}{\frac{dx}{\cos (x-a)\cos (x-b)}=}\\\end{array} \)
Solution:
\(\begin{array}{l}\int_{{}}^{{}}{\frac{dx}{\cos (x-a)\cos (x-b)}}\\ =\frac{1}{\sin (a-b)}\int_{{}}^{{}}{\frac{\sin \left\{ (x-b)-(x-a) \right\}}{\cos (x-a)\,.\,\cos (x-b)}\,dx}\\ =\frac{1}{\sin (a-b)}\int_{{}}^{{}}{\left\{ \frac{\sin (x-b)}{\cos (x-b)}-\frac{\sin (x-a)}{\cos (x-a)} \right\}dx}\\ =\text{cosec}\,(a-b)\log \frac{\cos (x-a)}{\cos (x-b)}+c\end{array} \)
Problem 2:
\(\begin{array}{l}\int_{{}}^{{}}{\frac{dx}{\sqrt{x+a}+\sqrt{x+b}}}=\\\end{array} \)
Solution:
\(\begin{array}{l}\int_{{}}^{{}}{\frac{dx}{\sqrt{x+a}+\sqrt{x+b}}=\int_{{}}^{{}}{\frac{\sqrt{x+a}-\sqrt{x+b}}{(x+a)-(x+b)}\,dx}}\\ =\frac{1}{(a-b)}\int_{{}}^{{}}{{{(x+a)}^{1/2}}dx}-\frac{1}{(a-b)}\int_{{}}^{{}}{{{(x+b)}^{1/2}}dx}\\ =\frac{2}{3(a-b)}[{{(x+a)}^{3/2}}-{{(x+b)}^{3/2}}]+c\end{array} \)
Problem 3:
\(\begin{array}{l}\int_{{}}^{{}}{\frac{{{x}^{3}}-x-2}{(1-{{x}^{2}})}\ dx=}\\\end{array} \)
Solution:
\(\begin{array}{l}\int_{{}}^{{}}{\frac{{{x}^{3}}-x-2}{(1-{{x}^{2}})}\,dx}\\=\int_{{}}^{{}}{\frac{-x(1-{{x}^{2}})}{(1-{{x}^{2}})}\,dx-\int_{{}}^{{}}{\frac{2}{1-{{x}^{2}}}\,dx}}\\=-\int_{{}}^{{}}{x\,dx}-2\int_{{}}^{{}}{\frac{1}{1-{{x}^{2}}}\,dx\\=\frac{-{{x}^{2}}}{2}+\log \left(\frac{x-1}{x+1}\right)+c.}\end{array} \)
Problem 4:
\(\begin{array}{l}\int_{{}}^{{}}{\frac{{{\sin }^{8}}x-{{\cos }^{8}}x}{1-2{{\sin }^{2}}x{{\cos }^{2}}x}\ dx=}\\\end{array} \)
Solution:
\(\begin{array}{l}\int_{{}}^{{}}{\frac{{{\sin }^{8}}x-{{\cos }^{8}}x}{1-2{{\sin }^{2}}x{{\cos }^{2}}x}\,dx}\\ =\int_{{}}^{{}}{\frac{({{\sin }^{4}}x+{{\cos }^{4}}x)({{\sin }^{4}}x-{{\cos }^{4}}x)}{{{({{\sin }^{2}}x+{{\cos }^{2}}x)}^{2}}-2{{\sin }^{2}}x{{\cos }^{2}}x}}\,dx\\ =\int_{{}}^{{}}{({{\sin }^{4}}x-{{\cos }^{4}}x)\,dx}\\ =\int_{{}}^{{}}{({{\sin }^{2}}x+{{\cos }^{2}}x)({{\sin }^{2}}x-{{\cos }^{2}}x)\,dx}\\ =\int_{{}}^{{}}{({{\sin }^{2}}x-{{\cos }^{2}}x)\,dx}\\=\int_{{}}^{{}}{-\cos 2x\,dx=-\frac{\sin 2x}{2}+c}\end{array} \)
Problem 5:
\(\begin{array}{l}\int_{{}}^{{}}{\frac{{{x}^{2}}dx}{{{(a+bx)}^{2}}}}=\\\end{array} \)
Solution:
Put a + bx = t ⇒ x = (t – a)/b and dx = dt/b
\(\begin{array}{l}I={{\int_{{}}^{{}}{\left( \frac{t-a}{b} \right)}}^{2}}\times \frac{1}{{{t}^{2}}}\frac{dt}{b}\\ =\frac{1}{{{b}^{2}}}\int_{{}}^{{}}{\left( 1-\frac{2a}{t}+{{a}^{2}}.{{t}^{-2}} \right)}\,dt\\=\frac{1}{{{b}^{2}}}\left[ t-2a\,\,\log t-\frac{{{a}^{2}}}{t} \right]\\ =\frac{1}{{{b}^{2}}}\left[ x+\frac{a}{b}-\frac{2a}{b}\log (a+bx)-\frac{{{a}^{2}}}{b}\frac{1}{(a+bx)} \right]\\\end{array} \)
Problem 6: Solve
\(\begin{array}{l}\int{\frac{2\cos x+3\sin x}{4\cos x+5\sin x}}\,dx\end{array} \)
Solution:
Problem of type
\(\begin{array}{l}\int{\frac{a\cos x+b\sin x+p}{c\cos x+d\sin x+q}}\,dx,\int{\frac{a{{e}^{x}}+b{{e}^{-x}}+c}{d{{e}^{x}}+f{{e}^{-x}}+h}}\,dx\end{array} \)
can be solved by \(\begin{array}{l}Nr=nDr+mDr'\end{array} \)
Now,
Let 2 cos x + 3 sin x = a( 4 cos x + 5 sin x) + b(-4 sin x + 5 cos x)
Solving by comparing, we get
\(\begin{array}{l}a=\frac{23}{41}\,\,\,\,\,\,b=\frac{-2}{41}\end{array} \)
\(\begin{array}{l}\therefore I=\int{\frac{23}{41}-\frac{2}{41}\left( \frac{-4\sin x+5\cos x}{4\cos x+5\sin x} \right)dx}\end{array} \)
\(\begin{array}{l}=\frac{23}{41}x-\frac{2}{41}\ell n\left| 4\cos x+5\sin x \right|+c\end{array} \)
Problem 7: Find area between y2 ≤ 4x, x2 + y2 ≥ 2x and x ≤ y + 2 in first quadrant.
Answer:
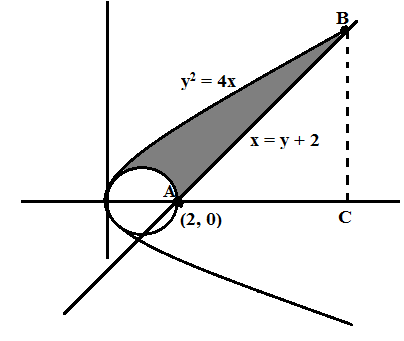
\(\begin{array}{l}A=\int\limits_{0}^{{{\left( \sqrt{3}+1 \right)}^{2}}}{\sqrt{4x}\,\,dx-} ar(semicircle) – ar(\triangle ABC)\end{array} \)
\(\begin{array}{l}=\sqrt{4}\left[ \frac{2{{x}^{3/2}}}{3} \right]_{0}^{{{\left( \sqrt{3}+1 \right)}^{2}}}-\frac{\pi }{2}-\frac{1}{2}{{\left( \sqrt{3}+1 \right)}^{2}}2\left( \sqrt{3}+1 \right)\end{array} \)
\(\begin{array}{l}=\frac{{{\left( \sqrt{3}+1 \right)}^{3}}}{3}-\frac{\pi }{2}\end{array} \)
Most Important Questions from Definite Integration for JEE Advanced
Frequently Asked Questions
Q1
What do you mean by integration in maths?
Integration is the process of finding the antiderivative of a function.
Q2
What is the integral of x?
The integral of x = (x2/2) + C, where C is the constant of integration.
Q3
What is the integral of sin x?
Integral of sin x =-cos x + C
Q4
Give two applications of integration.
Integration is used to find the area under a curve. It is also used to find the velocity and trajectory of a satellite.
Comments