Trigonometry is a measurement of a triangle, and it is included with inverse functions. sin-1x, cos-1 x, tan-1 x etc., represent angles or real numbers, and their sine is x, cosine is x, and tangent is x, given that the answers are numerically the smallest available. They are also written as arc sin x, arc cos x etc.
If there are two angles, one positive and another negative, having the same numerical value, then a positive angle should be taken. In this article, we will explain the topic of “inverse trigonometric functions”, important formulas and some solved problems.
Principal Values and Domain of Inverse Trigonometric Functions

Formulas of Inverse Trigonometric Functions
Given below are some basic formulas for the inverse of trigonometric functions:
\(\begin{array}{l}\sin^{-1} (\frac{1}{x}) = \csc ^{-1} x\end{array} \)
\(\begin{array}{l}\cos ^{-1} (\frac{1}{x}) = \sec ^{-1} x\end{array} \)
\(\begin{array}{l}\tan ^{-1} (\frac{1}{x}) = \cot ^{-1} x\end{array} \)
\(\begin{array}{l}\sin ^{-1} (-x) = – \sin ^{-1} x\end{array} \)
\(\begin{array}{l}\tan ^{-1} x + \cot ^{-1} x = \frac{\pi}{2}\end{array} \)
\(\begin{array}{l}\sin ^{-1} x + \cos ^{-1} x = \frac{\pi}{2}\end{array} \)
\(\begin{array}{l}\csc ^{-1} x + \sec ^{-1} x = \frac{\pi}{2}\end{array} \)
\(\begin{array}{l}\tan ^{-1} x + \tan ^{-1} y = \tan ^{-1} (\frac{x + y}{1 – xy})\end{array} \)
\(\begin{array}{l}\tan ^{-1} x – \tan ^{-1} y = \tan ^{-1} (\frac{x + y}{1 – xy})\end{array} \)
\(\begin{array}{l}2 \tan ^{-1} x = \sin ^{-1} (\frac{2x}{1 + x^2}) = \cos ^{-1} (\frac{1 – x^2}{1 + x^2}) = \tan ^{-1}(\frac{2x}{1 – x^2})\end{array} \)
Graphs of All Six Inverse Circular Functions
(1) Arc Sin x
Let y = sin-1 x, |x| ≤1, y ∈ [(-π)/2, π/2]
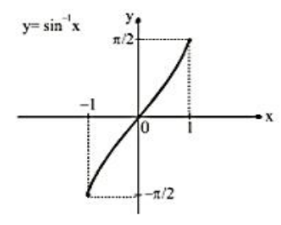
| Important Points:
(i) sin-1 x is bounded in [(-π)/2, π/2].
(ii) sin-1 x is an odd function (symmetric about the origin).
(iii) sin-1 x is an increasing function in its domain.
(iv) Maximum value of sin-1 x = π/2, occurs at x = 1, and minimum value of sin-1 x = (-π)/2, occurs at x = -1.
(v) sin-1 x is a periodic function. |
(2) Arc Cos x
Let y = cos-1 x, |x| ≤ 1, y ∈[0 , π].
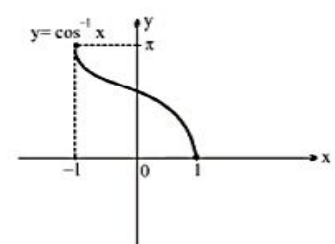
| Important Points:
(i) cos-1 x is bounded in [0, π].
(ii) cos-1 x is neither an odd nor even function.
(iii) cos-1 x is a decreasing function in its domain.
(iv) Maximum value of cos-1 x = π, occurs at x = -1, and minimum value of cos-1 x = 0, occurs at x = 1.
(v) cos-1x is a periodic function. |
(3) Arc tan x
Let y = tan-1 x, x ϵ R , y ∈ ((-π)/2, π/2).
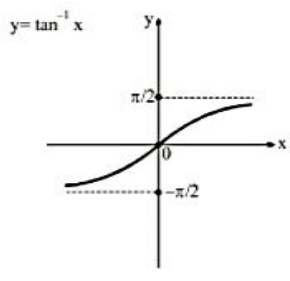
| Important Points:
(i) tan-1 x is bounded in ((-π)/2,π/2).
(ii) tan-1 x is an odd function (symmetric about x axis).
(iii) tan-1 x is an increasing function in its domain.
(iv) Maximum and minimum value is not defined for the tan-1 x.
(v) tan-1 x is a periodic function. |
(4) Arc cot x
Let y = cot-1 x, x ϵ R, y ∈(0 , π).
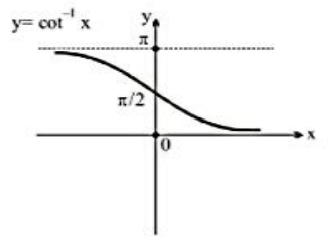
| Important Points:
(i) cot-1 x is bounded in (0, π).
(ii) cot-1 x is neither an odd nor even function.
(iii) cot-1 x is a decreasing function in its domain.
(iv) Maximum and minimum value is not defined for the cot-1 x.
(v) cot-1 x is a periodic function. |
(5) Arc Sec x
Let y = sec-1 x, |x| ≥ 1 , y ∈ [0, π/2) ∪ (π/2, π].
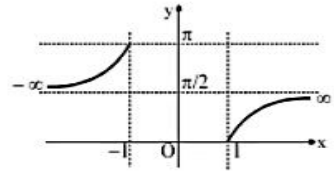
| Important points:
(i) sec-1 x is bounded in [0, π].
(ii) sec-1 x is neither an odd nor even function.
(iii) sec-1 x is an increasing function in two different intervals.
(iv) Maximum value of sec-1 x is π, occurs at x = -1, and minimum value of the sec-1 x is -π, occurs at x = 1.
(v) sec-1 x is a periodic function. |
(6) Arc cosec x
Let y = cosec-1 x, |x|≥1 , y ∈ [-π/2,0) ∪ (0, π/2].
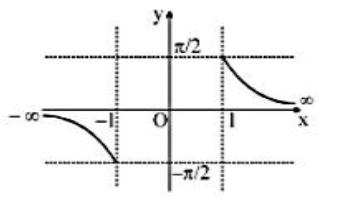
| Important Points:
(i) cosec-1x is bounded in [-π/2, π/2].
(ii) cosec-1 x is an odd function(symmetric about origin).
(iii) cosec-1 x is a decreasing function in two different intervals.
(iv) Maximum value of cosec-1 x is π/2, occurs at x = 1, and minimum value of the cosec-1 x is –π/2, occurs at x = -1.
(v) cosec-1 x is a periodic function. |
Different Techniques for Graphs of Inverse Trigonometric Functions
Solved Examples
Example 1: Find the value of sin(2 sin-1 3/5).
Solution: let sin-1 3/5= A
⇒ sin A = 3/5, cos A = 4/5
⇒ sin (2sin-1 3/5) = sin 2A = 2.sin A.cos A = 2.3/5.4/5=24/25.
Example 2: Find the value of cos(sin-14/5 – cos-1 4/5).
Solution: Let sin-1 4/5 = A and cos-1 4/5 = B
⇒ sin A = 4/5 and cos B = 4/5
⇒ cos A = 3/5 and sin B = 3/5
⇒ cos(sin-1 4/5 – cos-1 4/5)
[Using cos(A-B) = cos A cos B + sin A sin B]
⇒ 4/5 x 3/5 + 4/5 x 3/5 = 24/25.
Example 3: Show that
\(\begin{array}{l}sin^{-1}(2x \sqrt{1 – x^2}) = 2 cos ^{-1}(x), \frac{-1}{\sqrt{2}} \leq x \leq 1\end{array} \)
.
Solution:
Given
\(\begin{array}{l}sin^{-1}(2x \sqrt{1 – x^2}) = 2 cos ^{-1}(x)\end{array} \)
Let us consider
\(\begin{array}{l}x = \cos \theta\end{array} \)
Then,
\(\begin{array}{l}cos^{-1} x = \theta\end{array} \)
We have
\(\begin{array}{l}sin^{-1}(2x \sqrt{1 – x^2}) = sin^{-1}(2 cos \theta \sqrt{1 – \cos^2 \theta})\end{array} \)
Formula:
\(\begin{array}{l}sin^2 \theta = 1 – cos^2 \theta\end{array} \)
\(\begin{array}{l}=sin^{-1} (2 cos \theta \sqrt{sin ^2 \theta})\end{array} \)
\(\begin{array}{l}=sin^{-1}(2 cos \theta sin \theta)\end{array} \)
Formula:
\(\begin{array}{l}sin 2 \theta = 2 sin \theta cos \theta\end{array} \)
\(\begin{array}{l}=sin^{-1}(sin 2 \theta)\end{array} \)
\(\begin{array}{l}=2 \theta\end{array} \)
\(\begin{array}{l}= 2 cos ^{-1} (x)\end{array} \)
Example 4: Write
\(\begin{array}{l}tan^{-1} (\frac{cos y}{1 – sin y}), \frac{-\pi}{2} < y < \frac{\pi}{2}\end{array} \)
in the simplest form.
Solution:
Given,
\(\begin{array}{l}tan^{-1} (\frac{cos y}{1 – sin y})\end{array} \)
We are going to simplify the given
\(\begin{array}{l}tan^{-1} \frac{cos y}{1 – sin y}\end{array} \)
Formula:
\(\begin{array}{l}cos y = sin (\frac{\pi}{2} – y)\end{array} \)
and \(\begin{array}{l}sin y = cos (\frac{\pi}{2} – y)\end{array} \)
\(\begin{array}{l}tan^{-1}( \frac{cos y}{1 – sin y}) = tan^{-1}\frac{sin(\frac{\pi}{2} – y)}{1 – cos (\frac{\pi}{2} – y)}\end{array} \)
\(\begin{array}{l}=tan ^{-1} (tan (\frac{\pi}{4} + \frac{y}{2})\end{array} \)
\(\begin{array}{l}=\frac{\pi}{4} + \frac{y}{2}\end{array} \)
Example 5:
\(\begin{array}{l}\sin ({{\cot}^{-1}}x)=\end{array} \)
Solution:
Let
\(\begin{array}{l}{{\cot}^{-1}}x=\theta \,\,\Rightarrow \,\,x=\cot \theta \\ \text{Now}\ \cos ec\,\theta =\sqrt{1+{{\cot}^{2}}\theta }=\sqrt{1+{{x}^{2}}}\\ \,\,\,\sin \theta =\frac{1}{\cos ec\,\theta }=\frac{1}{\sqrt{1+{{x}^{2}}}}\,\,\\ \Rightarrow \,\theta ={{\sin}^{-1}}\frac{1}{\sqrt{1+{{x}^{2}}}}\\ \text{Hence,}\ \sin \,({{\cot}^{-1}}x)\,=\sin \,\left( {{\sin}^{-1}}\frac{1}{\sqrt{1+{{x}^{2}}}} \right)\\ =\frac{1}{\sqrt{1+{{x}^{2}}}}={{(1+{{x}^{2}})}^{-1/2}}\end{array} \)
Example 6:
\(\begin{array}{l}{{\tan}^{-1}}\left(\frac{\sqrt{1+{{x}^{2}}}-1}{x} \right)=\end{array} \)
.
Solution:
\(\begin{array}{l}{{\tan }^{-1}}\left(\frac{\sqrt{1+{{x}^{2}}}-1}{x} \right)={{\tan}^{-1}}\left[\frac{\sqrt{1+{{\tan }^{2}}\theta}-1}{\tan \theta} \right]\\(\text{Putting}\ x=\tan \theta)\\ ={{\tan}^{-1}}\left[ \frac{\sec \theta -1}{\tan \theta} \right]\\={{\tan}^{-1}}\left[\frac{1-\cos \theta}{\sin \theta} \right]\\ ={{\tan}^{-1}}\left[\frac{2\,{{\sin}^{2}}\frac{\theta}{2}}{2\,\sin \frac{\theta}{2}\cos \frac{\theta}{2}} \right]\\ ={{\tan}^{-1}}\tan \frac{\theta}{2}=\frac{\theta}{2}=\frac{1}{2}{{\tan }^{-1}}x\end{array} \)
Example 7:
\(\begin{array}{l}{{\sin}^{-1}}\left[x\sqrt{1-x}-\sqrt{x}\sqrt{1-{{x}^{2}}} \right]=\end{array} \)
.
Solution:
Let
\(\begin{array}{l}x=\sin \theta \text{and}\ \sqrt{x}=\sin \varphi\\ \text{Hence,}\ {{\sin}^{-1}}(x\sqrt{1-x}-\sqrt{x}\,\sqrt{1-{{x}^{2}}})\\ ={{\sin}^{-1}}(\sin \theta \sqrt{1-{{\sin}^{2}}\varphi }-\sin \varphi \sqrt{1-{{\sin}^{2}}\theta})\\ ={{\sin }^{-1}}(\sin \theta \cos \varphi -\sin \varphi \cos \theta )\\={{\sin}^{-1}}\sin \,(\theta -\varphi)\\ =\theta -\varphi ={{\sin}^{-1}}(x)-{{\sin}^{-1}}(\sqrt{x})\end{array} \)
Example 8:
\(\begin{array}{l}\text{If}\ {{\tan}^{-1}}\frac{1-x}{1+x}=\frac{1}{2}{{\tan}^{-1}}x,\ \text{then}\ x=\end{array} \)
.
Solution:
We have
\(\begin{array}{l}{{\tan}^{-1}}\,\frac{1-x}{1+x}=\frac{1}{2}{{\tan}^{-1}}x\\ \Rightarrow \,\,{{\tan}^{-1}}\,\left[ \frac{1-\tan \theta}{1+\tan \theta} \right]=\frac{1}{2}\theta \\ (\text{Putting}\ x=\tan \theta )\\ \Rightarrow \,\,{{\tan}^{-1}}\,\left[\frac{\tan \frac{\pi}{4}-\tan \theta}{1+\tan \frac{\pi}{4}\tan \theta} \right]\\ =\frac{\theta}{2}\\ \Rightarrow \,\,{{\tan}^{-1}}\tan \,\left(\frac{\pi }{4}-\theta \right)=\frac{\theta}{2}\,\,\Rightarrow \,\,\frac{\pi}{4}-\theta =\frac{\theta}{2}\\ \Rightarrow \,\,\theta =\frac{\pi}{6}={{\tan}^{-1}}x\,\,\Rightarrow \,\,x=\tan \frac{\pi}{6}=\frac{1}{\sqrt{3}}\end{array} \)
Example 9: The smallest and the largest values of
\(\begin{array}{l}{{\tan}^{-1}}\left( \frac{1-x}{1+x} \right)\text{ },\,\,0\le x\le 1\end{array} \)
are
Solution:
We have,
\(\begin{array}{l}{{\tan }^{-1}}\,\left( \frac{1-x}{1+x} \right)\\={{\tan }^{-1}}1-{{\tan }^{-1}}x\\=\frac{\pi }{4}-{{\tan }^{-1}}x \\ \text{Since}\ 0\le x\le 1\,\,\\ \Rightarrow \,\,0\le {{\tan }^{-1}}x\le \frac{\pi }{4}\\ \Rightarrow \,\,0\ge -{{\tan }^{-1}}x\ge \frac{-\pi }{4}\\ \Rightarrow \,\,\frac{\pi }{4}\ge \frac{\pi }{4}-{{\tan }^{-1}}x\ge 0\\ \Rightarrow \,\,\frac{\pi }{4}\ge {{\tan }^{-1}}\left( \frac{1-x}{1+x} \right)\ge 0\end{array} \)
Video Lessons
Domain, Range and Graph of Inverse Trigonometric Functions
Inverse Trigonometric Functions Video Lesson
Properties of Inverse Trigonometric Functions – 1
Properties of Inverse Trigonometric Functions – 2
Sum, Difference and Multiple Angle Formulas – ITF
ITF – Most Important JEE Main Questions
ITF – Top 10 Most Important JEE Questions
Frequently Asked Questions
Q1
What are the 6 inverse trigonometric functions?
Arcsine, Arccosine, Arctangent, Arccotangent, Arcsecant, and Arccosecant are the 6 inverse trigonometric functions.
Q2
What is the range of cos-1x?
The range of cos-1x is [0, π].
Q3
What is the domain of sin-1x?
The domain of sin-1x is [-1, 1].
Q4
What is the domain of cos-1x?
The domain of cos-1x is [-1, 1].

















Comments