JEE Main 2020 solved shift 1 Maths paper with solutions are available on this page. Students are recommended to revise these questions and understand how the solutions are formed so that they can improve their problem-solving skills. These question paper given here will help candidates to understand the question types along with the paper pattern and the difficulty level of questions from each chapter. Students can easily download the solutions in PDF format for free.
JEE Advanced 2020 Question Paper
January 9 Shift 1 – Maths
January 9 Shift 1 – Maths
Question 1. If C be the centroid of the triangle having vertices (3, -1), (1, 3) and (2, 4). Let P be the point of intersection of the lines x + 3y – 1 = 0 and 3x – y + 1 = 0, then the line passing through the points C and P also passes through the point:
a) (-9, -7)
b) (-9, -6)
c) (7, 6)
d) (9, 7)
Coordinates of C are ((3+1+2)/3 , (-1+3+4)/3) = (2,2)
Point of intersection of two lines
x + 3y – 1 = 0 and 3x – y + 1 = 0 is P(-1/5, 2/5).
Equation of line CP is 8x-11y+6 = 0
Point (-9,-6) lies on CP.
Answer:(b)
Question 2. The product 21/4×41/16×81/48×161/128… ..∞ to is equal to
a) 21/4
b) 2
c) 21/2
d) 1
21/4×41/16×81/48×161/128… ∞= 21/4×22/16×23/48×….∞
21/4×21/8×21/16×… ∞= 21/4 + 1/8 + 1/16 …∞
\(\begin{array}{l}2^{\left ( \frac{\frac{1}{4}}{1-\frac{1}{2}} \right )}\end{array} \)
= √2
Answer: (c)
Question 3. A spherical iron ball of 10 cm radius is coated with a layer of ice of uniform thickness that melts at the rate of 50 cm3/min. When the thickness of ice is 5 cm, then the rate (in cm/min.) at which the thickness of ice decreases, is:
a) 5/6π
b) 1/54π
c) 1/36π
d) 1/18π
Let thickness of ice be 𝑥 cm.
Therefore, net radius of sphere = (10+𝑥) cm
Volume of sphere V = (4π/3)(10+𝑥)3
⇒dV/dt = 4𝜋(10+𝑥)2 dx/dt
At x = 5, dV/dt = 50 cm3/min
⇒ 50 = 4π×225×𝑑x/𝑑t
dx/dt = 1/18π cm/min
Answer: (d)
Question 4. Let f be any function continuous on [𝑎,𝑏] and twice differentiable on (𝑎,𝑏). If for all 𝑥∈(𝑎,𝑏),f’(x)> 0 and f’’(x) < 0, then for any c ∈ (a,b), (f(c) – f(a)])- (f(b) – f(c)]) is greater than:
a) (b-c)/(c-a)
b) 1
c) (c-a)/(b-c)
d) (b+a)/(b-a)
c∈(a,b) and f is twice differentiable and continuous function on (𝑎,𝑏)
LMVT is applicable.
For p ∈ (a,c) f’(𝑝) = (f(𝑐)−𝑓(𝑎))/(𝑐−𝑎)
For q ∈ (c,b), f’(q) = (f(b)-f(c)/(b-c)
f’’(x) < 0 f’(x) is decreasing
f’(p) > f’(q)
(f(c) – f(a))/(c-a) > (f(b) – f(c))/(b-c)
(f(c) – f(a))/ (f(b) – f(c)) > (c-a)/(b-c) (as f’(x)>0 f(x) is increasing.
Answer: (c)
Question 5. The value of cos3 (π/8) cos (3π/8) + sin3 (π/8) sin (3π/8) is:
a) 1/4
b) 1/2√2
c) 1/2
d) 1/√2
cos3 (π/8) cos (3π/8) + sin3 (π/8) sin (3π/8) = cos3 (π/8) [ 4 cos3 (π/8) – 3 cos (π/8)] + sin3 (π/8)[ 3 sin (π/8) – 4 sin3 (π/8)]
= 4[cos6 (π/8) – sin6 (π/8)] + 3[sin4 (π/8) – cos4(π/8)]
= 4[cos2 (π/8) – sin2 (π/8)] [cos4 (π/8) + sin4 (π/8) + cos2 (π/8) sin2 (π/8)] -3[cos2 (π/8) – sin2 (π/8)]
= [cos2 (π/8) – sin2 (π/8)][4(1-cos2(π/8) sin2 (π/8) -3]
= cos (π/4)[1- sin2 (π/4)]
= 1/2√2
Answer: (c)
Question 6. The number of real roots of the equation, e4x + e3x – 4e2x + 1 = 0 is
a) 3
b) 4
c) 1
d) 2
e4x + e3x – 4e2x + ex + 1 = 0
e2x + ex – 4 + (1/ex) + (1/e2x) = 0
(e2x + (1/e2x)) + (ex + 1/ex) – 4 = 0
(ex + 1/ex)2 – 2 + (ex + 1/ex) – 4 = 0
Let (ex + 1/ex) = u
Then u2 + u – 6 = 0
u = 2, -3
u ≠ -3 as u > 0 ( since ex > 0)
(ex + 1/ex) = 2
(ex – 1)2 = 0
ex = 1
x = 0
Hence, only one real solution is possible.
Answer: (c)
Question 7. The value of \(\begin{array}{l}\int_{0}^{2\pi }\frac{x\sin ^{8}x}{\sin ^{8}x+\cos ^{8}x}dx\end{array} \)
is equal to
a) 2
b) 4
c) 22
d) π2
Let I =
\(\begin{array}{l}\int_{0}^{2\pi }\frac{x\sin ^{8}x}{\sin ^{8}x+\cos ^{8}x}dx\end{array} \)
…(i)
I =
\(\begin{array}{l}\int_{0}^{2\pi }\frac{(2\pi -x)\sin ^{8}(2\pi -x)}{\sin ^{8}(2\pi -x)+\cos ^{8}(2\pi -x)}dx\end{array} \)
=
\(\begin{array}{l}\int_{0}^{2\pi }\frac{(2\pi -x)\sin ^{8}x}{\sin ^{8}x+\cos ^{8}x}dx\end{array} \)
..(ii)
Adding (i) and (ii)
\(\begin{array}{l}2I = 2\pi \int_{0}^{2\pi }\frac{\sin ^{8}x}{\sin ^{8}x+\cos ^{8}x}dx\end{array} \)
\(\begin{array}{l}I = \pi \int_{0}^{2\pi }\frac{\sin ^{8}x}{\sin ^{8}x+\cos ^{8}x}dx\end{array} \)
\(\begin{array}{l}I = 4\pi \int_{0}^{\frac{\pi }{2} }\frac{\sin ^{8}x}{\sin ^{8}x+\cos ^{8}x}dx\end{array} \)
…(iii)
\(\begin{array}{l}I = 4\pi \int_{0}^{\frac{\pi }{2} }\frac{\sin ^{8}(\frac{\pi }{2}-x)}{\sin ^{8}(\frac{\pi }{2}-x)+\cos ^{8}(\frac{\pi }{2}-x)}dx\end{array} \)
=
\(\begin{array}{l}4\pi \int_{0}^{\frac{\pi }{2} }\frac{\cos ^{8}x}{\sin ^{8}x+\cos ^{8}x}dx\end{array} \)
..(iv)
Adding (iii) and (iv), we get:
\(\begin{array}{l}I = 2\pi \int_{0}^{\frac{\pi }{2} }1dx = 2\pi \times \frac{\pi }{2}=\pi ^{2}\end{array} \)
Answer: (d)
Question 8. If for some α and β in 𝑅, the intersection of the following three planes
x + 4y − 2z = 1
x + 7y − 5z =β
x + 5y + αz = 5
is a line in 𝑅3, then α+β is equal to:
a) 0
b) 10
c) -10
d) 2
The given planes intersect in a line
D = Dx = Dy = Dz = 0
D = 0
\(\begin{array}{l}\begin{vmatrix} 1 &4 & -2\\ 1 &7 & -5\\ 1 & 5& \alpha \end{vmatrix} = 0\end{array} \)
7α + 25 – 4α -20 + 4 = 0
α= -3
Dz = 0
\(\begin{array}{l}\begin{vmatrix} 1 &4 & 1\\ 1 &7 & \beta \\ 1 & 5& 5 \end{vmatrix} = 0\end{array} \)
35 – 5β -20 + 4β -2 = 0
β= 13
α+ β= 10
Answer: (b)
Question 9. If e1 and e2 are the eccentricities of the ellipse, (x2/18) + (y2/4) = 1 and the hyperbola, (x2/9) -(y2/4) =1 respectively and (e1 , e2) is a point on the ellipse, 15x2 + 3y2 = k. Then k is equal to:
a) 14
b) 15
c) 17
d) 16
e1 = √(1-(4/18))
= √7/3
e2 = √(1+(4/9))
= √13/3
Since (e1, e2) lies on the ellipse 15x2 + 3y2 = k
15×(7/9) + 3×(13/9) = k
k = 16
Answer: (d)
Question 10. If f(x) =
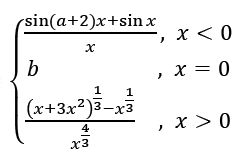
is continuous at x = 0 then a + 2b is equal to:
a) -2
b) 1
c) 0
d) 1
f(x) is continuous at x = 0
\(\begin{array}{l}\lim_{x\to0^{-}}f(x)= b= \lim_{x\to0^{+}}f(x)\end{array} \)
\(\begin{array}{l}b = \lim_{h\to0}f(0+h)= \lim_{h\to0}\frac{(h+3h^{2})^{\frac{1}{3}}-h^{\frac{1}{3}}}{h^{\frac{4}{3}}}\end{array} \)
\(\begin{array}{l}b = \lim_{h\to0} \frac{h^{\frac{1}{3}\left [ (1+3h)^{\frac{1}{3}}-1\right ]}}{h\frac{4}{3}}\end{array} \)
\(\begin{array}{l}b = \lim_{h\to0} \frac{(1+3h)^{\frac{1}{3}}-1}{h}\end{array} \)
\(\begin{array}{l}b = \lim_{h\to0} \frac{1}{3}(1+3h)^{\frac{-2}{3}}\times 3\end{array} \)
Or b = 1.
\(\begin{array}{l}\lim_{x\to0^{-}} f(x)=1\Rightarrow \lim_{h\to0}\frac{\sin ((a+2)(-h))+\sin (-h)}{-h}= 1\end{array} \)
a + 3 = 1 a = -2
a + 2b = 0
Answer: (c)
Question 11. If the matrices A = \(\begin{array}{l}\begin{bmatrix} 1 & 1 &2 \\ 1& 3&4 \\ 1 & -1&3 \end{bmatrix}\end{array} \)
, B = adj A and C = 3A, then \(\begin{array}{l}\frac{\left | adj \: B \right |}{\left | C \right |}\end{array} \)
is equal to
a) 16
b) 2
c) 8
d) 72
A =
\(\begin{array}{l}\begin{bmatrix} 1 & 1 &2 \\ 1& 3&4 \\ 1 & -1&3 \end{bmatrix}\end{array} \)
\(\begin{array}{l}\left | A \right |= \begin{vmatrix} 1 & 1 & 2\\ 1& 3 & 4\\ 1& -1 & 3 \end{vmatrix}\end{array} \)
= 13 + 1 – 8
= 6
B = adj(A) ǀadj Bǀ = ǀadj (adj A)ǀ = ǀAǀ4 = 64
ǀCǀ = ǀ3Aǀ = 33ǀAǀ = 33 × 6
\(\begin{array}{l}\frac{\left | adj \: B \right |}{\left | C \right |}\end{array} \)
= 64/(33×6)
= 8
Answer: (c)
Question 12. A circle touches the y-axis at the point (0,4) and passes through the point (2,0). Which of the following lines is not a tangent to the circle?
a) 4x−3y+17 = 0
b) 3x+4y−6 = 0
c) 4x+3y−8 = 0
d) 3x−4y−24 = 0

OD2 = OA×OB
16 = 2× OB
OB = 8
AB = 6
AM = 3
CM = 4
CA = 5
OM = 5
Centre will be (5,4) and radius is 5
Now checking all the options
Option (c) is not a tangent.
4x+3y−8=0
(20 + 12 – 8)/√(32 + 42) = 24/5
(p ≠ r)
Answer: (c)
Question 13. Let 𝑧 be a complex number such that \(\begin{array}{l}{\left | \frac{z-i}{z+2i} \right |}= 1\end{array} \)
and \(\begin{array}{l}{\left | z\right |}= \frac{5}{2}\end{array} \)
. Then the value of \(\begin{array}{l}{\left | z+3i\right |}\end{array} \)
is:
a) √10
b) 7/2
c) 15/4
d) 2√3
If
\(\begin{array}{l}{\left | \frac{z-i}{z+2i} \right |}= 1\end{array} \)
and \(\begin{array}{l}{\left | z\right |}= \frac{5}{2}\end{array} \)
\(\begin{array}{l}{\left | z-i\right |} = {\left | z+2i\right |}\end{array} \)
y-1 = ± (y+2)
y-1 = -y-2
y = -1/2
ǀzǀ = 5/2
x2 + y2 = 25/4
x2 + y2 = 25/4
x2 + ¼ = 25/4
x = ±√6
\(\begin{array}{l}{\left | z+3i\right |} = \sqrt{(x^{2}+(y+3)^{2}}\end{array} \)
\(\begin{array}{l}{\left | z+3i\right |} = \frac{7}{2}\end{array} \)
Answer: (b)
Question 14. If f’(x) = tan -1 (sec x + tan x ), (-π/2) < x < (π/2), and f(0) = 0, then f(1) is equal to:
a) (π+1)/4
b) (π+2)/4
c) 1/4
d) (π-1)/4
f’(x) = tan-1 (sec x + tan x) = tan-1 ((1+ sin x)/cos x )
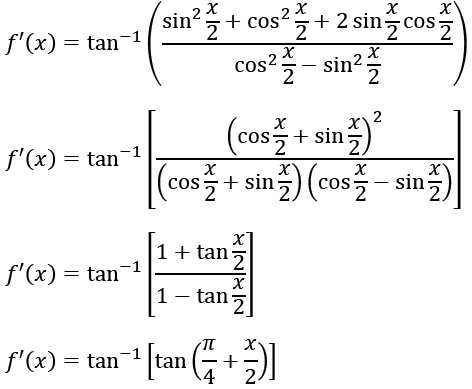
f’(x) = (π/4) + (x/2)
f(x) = (π/4) x+ (x2/4) +c
f(0) = 0
c = 0
f(1) = (π/4) + (1/4) = (π+1)/4
Answer: (a)
Question 15. Negation of the statement: ′√5 is an integer or 5 is irrational′ is:
a) √5 is irrational or 5 is an integer.
b) √5 is not an integer or 5 is not irrational.
c) √5 is an integer and 5 is irrational.
d) √5 is not an integer and 5 is not irrational.
p:√5 is an integer
q:5 is an irrational number
Given statement : (p∨q)
Required negation statement: ~(p∨q) = ~p∧ ~ q
′√5 is not an integer and 5 is not irrational’
Answer: (d)
Question 16. If for all real triplets (a,b,c), f(x) = a+ bx+ cx2; then \(\begin{array}{l}\int_{0}^{1}f(x)dx\end{array} \)
is equal to
a) 2(3f(1)+2f(1/2))
b) (1/3)(f(0)+f(1/2))
c) (1/2) (f(1)+3f(1/2))
d) (1/6)(f(0)+f(1)+4f(1/2))
f(x) = a+ bx + cx2
f(0) = a, f(1) = a + b + c
f(1/2) = (c/4) + (b/2) + a
\(\begin{array}{l}\int_{0}^{1}f(x)dx = \int_{0}^{1}(a+bx+cx^{2})dx = a+\frac{b}{2}+\frac{c}{3}\end{array} \)
= (1/6) (6a + 3b + 2c)
= (1/6) (a + (a + b + c) + (4a + 2b +c))
= (1/6)(f(0) + f(1) + 4f(1/2))
Answer: (d)
Question 17. If the number of five digit numbers with distinct digits and 2 at the 10th place is 336k, then k is equal to:
a) 8
b) 7
c) 4
d) 6

Total numbers that can be formed are = 8×8×7×6
= 8×336
k = 8
Answer (a)
Question 18. Let the observations xi(1 ≤ i ≤ 10) satisfy the equations, \(\begin{array}{l}\sum_{i=1}^{10}(x_{i}-5)=10\end{array} \)
and \(\begin{array}{l}\sum_{i=1}^{10}(x_{i}-5)^{2}=40\end{array} \)
. If μ and λ are the mean and the variance of observations, (x1-3),(x2-3)…..(x10-3) , then the ordered pair (μ,λ) is equal to:
a) (6,3)
b) (3,6)
c) (3,3)
d) (6,6)
Solution:
\(\begin{array}{l}\sum_{i=1}^{10}(x_{i}-5)=10\end{array} \)
\(\begin{array}{l}\sum_{i=1}^{10}x_{i}=60\end{array} \)
\(\begin{array}{l}\mu = \frac{\sum_{i=1}^{10}(x_{i}-3)}{10}=\frac{\sum_{i=1}^{10}x_{i}-30}{10} = 3\end{array} \)
Variance is unchanged, if a constant is added or subtracted from each observation.
λ= Var (xi-3)
= Var (xi-5)
=
\(\begin{array}{l}\frac{\sum_{i=1}^{10}(x_{i}-5)^{2}}{10}-\left ( \frac{\sum_{i=1}^{10}(x_{i}-5)}{10} \right )^{2}= \frac{40}{10}-(\frac{10}{10})^{2} = 3\end{array} \)
Answer (c)
Question 19. The integral \(\begin{array}{l}\int \frac{dx}{\left (x+4\right )^{\frac{8}{7}}\left (x-3 \right )^{\frac{6}{7}}}\end{array} \)
is equal to: (where C is a constant of integration)
a) \(\begin{array}{l}-\left ( \frac{x-3}{x+4} \right )^{-\frac{1}{7}}+ C\end{array} \)
b) \(\begin{array}{l}\frac{1}{2}\left ( \frac{x-3}{x+4} \right )^{\frac{3}{7}}+ C\end{array} \)
c) \(\begin{array}{l}\left ( \frac{x-3}{x+4} \right )^{\frac{1}{7}}+ C\end{array} \)
d) \(\begin{array}{l}-\frac{1}{13}\left ( \frac{x-3}{x+4} \right )^{-\frac{13}{7}}+ C\end{array} \)

Answer: (c)
Question 20. In a box, there are 20 cards out of which 10 are labelled as A and remaining 10 are labelled as B. Cards are drawn at random, one after the other and with replacement, till a second A-card is obtained. The probability that the second A-card appears before the third 𝐵-card is:
a) 15/16
b) 9/16
c) 13/16
d) 11/16
Here P(A) = P(B) = 12
Then, these following cases are possible AA, BAA, ABA, ABBA, BBAA, BABA
So, the required probability is = (1/4)+(1/8)+(1/8) +(1/16)+(1/16)+(1/16) = 11/16
Answer: (d)
Question 21. If the vectors \(\begin{array}{l}\vec{p} = (a+1)\hat{i}+a\hat{j}+a\hat{k}\end{array} \)
, \(\begin{array}{l}\vec{q} = a\hat{i}+(a+1)\hat{j}+a\hat{k}\end{array} \)
and \(\begin{array}{l}\vec{r} = a\hat{i}+a\hat{j}+(a+1)\hat{k}\end{array} \)
(a∈R) are coplanar and \(\begin{array}{l}3(\vec{p} .\vec{q})^{2}-\lambda \left |\vec{r}\times \vec{q} \right |^{2}=0\end{array} \)
then value of λ is
As vectors p, q and r are coplanar,
\(\begin{array}{l}\begin{vmatrix} (a+1) &a & a\\ a & (a+1)& a\\ a & a& (a+1) \end{vmatrix}=0\end{array} \)
R1 🡪 R1 + R2 + R3
\(\begin{array}{l}\begin{vmatrix} 3a+1 &3a+1 & 3a+1\\ a & a+1& a\\ a & a& a+1 \end{vmatrix}=0\end{array} \)
\(\begin{array}{l}(3a+1)\begin{vmatrix} 1 &1 & 1\\ a & a+1& a\\ a & a& a+1 \end{vmatrix}=0\end{array} \)
C2 🡪 C2 – C1 and C3 🡪 C3 – C1
\(\begin{array}{l}(3a+1)\begin{vmatrix} 1 &0 & 0\\ a & 1& 0\\ a & 0& 1 \end{vmatrix}=0\end{array} \)
3a + 1 = 0
a = -1/3

Answer: (1)
Question 22.The projection of the line segment joining the points (1,-1,3) and (2,-4,11) on the line joining the points (-1,2,3) and (3,-2,10) is __.
\(\begin{array}{l}\vec{AB} = \hat{i}-3\hat{j}+8\hat{k}\end{array} \)
\(\begin{array}{l}\vec{CD} = 4\hat{i}-4\hat{j}+7\hat{k}\end{array} \)
Projection of vector AB on vector CD =
\(\begin{array}{l}\frac{\vec{AB}.\vec{CD}}{\left | \vec{CD} \right |}=\frac{4+12+56}{\sqrt{4^{2}+4^{2}+7^{2}}}=\frac{72}{9}=8\end{array} \)
Answer: (8)
Question 23. The number of distinct solutions of the equation \(\begin{array}{l}log_{\frac{1}{2}}\left | \sin x \right |= 2-log_{\frac{1}{2}} \left | \cos x \right |\end{array} \)
in the interval [0, 2] is:

sin 2x = ±1/2

∴ We have 8 solutions for x ∈ [0,2]
Answer: (8)
Question 24. If for x ≥ 0,y = y(x) is the solution of the differential equation (1+x)dy = [(1+x)2+y-3]dx, y(2) = 0, then y(3) is equal to:
(1+x) dy/dx = [(1+x)2 + (y-3)]
(1+x) (dy/dx) -y = (1+x)2 -3
(dy/dx)-(1/1+x)y = 1+x – 3/(1+x)
I.F =
\(\begin{array}{l}e^{-\int \frac{1}{1+x}dx} = \frac{1}{1+x}\end{array} \)
\(\begin{array}{l}y\times \frac{1}{1+x} = \int 1-\frac{3}{(1+x)^{2}}dx\end{array} \)
y = x(1+x) + 3+c(1+x)
At x = 2, y = 0 we get
0 = 6+3+3c
c = -3
At x = 3,
y = x2 -2x
= 9-6
= 3
y(3) = 3
Answer: (3)
Question 25. The coefficient of x4 in the expansion of (1+x+x)10 is
General term of the given expression is given by
\(\begin{array}{l}\frac{10!}{p!q!r!}x^{q+2r}\end{array} \)
Here, q+2r =4
For p = 6, q = 4, r = 0, coefficient = 10!/(6!×4!) = 210
For p = 7, q = 2, r = 1, coefficient = 10!/(7!×2!×1!) = 360
For p = 8, q = 0, r = 2, coefficient = 10!/(8!×2!) = 45
Therefore, sum = 615
Answer (615)
Video Lessons – January 9 Shift 1 Maths
Download PDF 
carouselExampleControls112
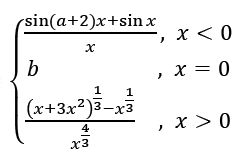

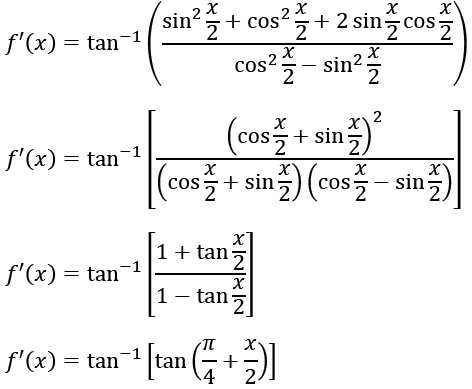
























Comments