IIT JEE is an examination conducted for admission into some of the top colleges in India. The examination is conducted in two levels- JEE Main and JEE Advanced. Students can find the solved paper of JEE Main 2020 Physics (Shift 1-2nd Sept) on this page. The subject experts at BYJU’S have solved all these questions. Students can also download these solutions from our website in PDF format.
JEE Main 2020 Physics Paper With Solutions Sep 2 Shift 1
September 2 Shift 1 – Physics
Question 1.The mass density of a spherical galaxy K varies as K/r over a large distance ‘r’ from its centre. In that region, a small star is in a circular orbit of radius R. Then the period of revolution, T depends on R as:
a) T2∝R
b) T2∝R3
c) T2∝ (1/R3)
d) T ∝R
a) T2∝R
b) T2∝R3
c) T2∝ (1/R3)
d) T ∝R
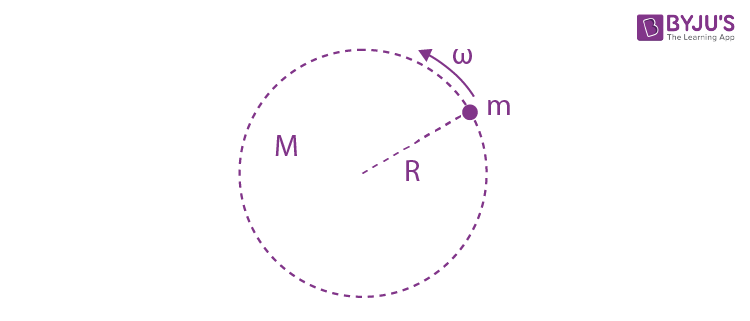
Mass of galaxy =
\(\begin{array}{l}\int_{0}^{R}\rho dv\end{array} \)
=
\(\begin{array}{l}\int_{0}^{R}\frac{k}{r}4\pi r^{2} dv\end{array} \)
\(\begin{array}{l}=4\pi k\int_{0}^{R}rdr\end{array} \)
\(\begin{array}{l}M=\frac{4\pi kR^{2}}{2}=k_{1}R^{2}\end{array} \)
\(\begin{array}{l}F =m\omega ^{2}R\end{array} \)
\(\begin{array}{l}\frac{GMm}{R^{2}}=m\omega ^{2}R\end{array} \)
\(\begin{array}{l}\frac{Gk_{1}R^{2}}{R^{2}}=\omega ^{2}R\end{array} \)
\(\begin{array}{l}\omega ^{2}=\frac{k_{2}}{R}\end{array} \)
\(\begin{array}{l}\omega =\sqrt{\frac{k_{2}}{R}}\end{array} \)
\(\begin{array}{l}T=\frac{2\pi }{\omega }=2\pi \sqrt{\frac{R}{k_{2}}}\end{array} \)
\(\begin{array}{l}T=k_{3}\sqrt{R}\end{array} \)
T2∝R
Answer:(a)
Question 2. An amplitude modulated wave is represented by the expression vm= 5(1 + 0.6 cos6280t )sin (211 x 104t) volts. The minimum and maximum amplitudes of the amplitude modulated wave are, respectively :
a)
b) 5V,8V
c) 3V,5V
d)
a)
\(\begin{array}{l}\frac{3}{2}V,5V\end{array} \)
b) 5V,8V
c) 3V,5V
d)
\(\begin{array}{l}\frac{5}{2}V,8V\end{array} \)
\(\begin{array}{l}\frac{A_{m}}{A_{c}}=0.6\end{array} \)
Vm = (5+3 cos 6280t) sin (211×104 t)
maximum Amp. = 5+3 = 8 V
minimum Amp. = 5–3 = 2 V
from the given option nearest value of minimum Amplitude = (5/2) V
Answer: (d)
Question 3. A spherical mirror is obtained as shown in the figure from a hollow glass sphere. If an object is positioned in front of the mirror, what will be the nature and magnification of the image of the object ? (Figure drawn as schematic and not to scale)
a) Erect, virtual and unmagnified
b) Inverted, real and magnified
c) Erect, virtual and magnified
d) Inverted, real and unmagnified
a) Erect, virtual and unmagnified
b) Inverted, real and magnified
c) Erect, virtual and magnified
d) Inverted, real and unmagnified
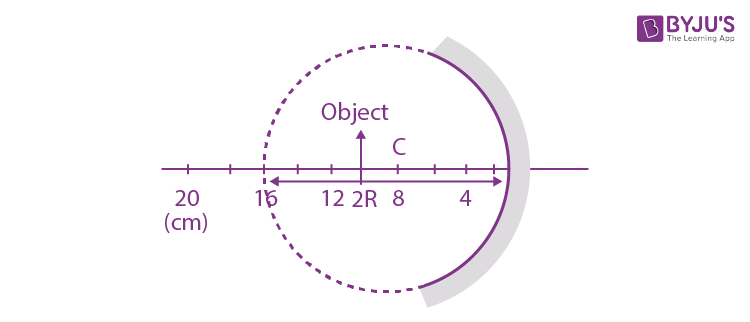
Therefore beyond C i.e -∞< u < C
Therefore real, inverted, and unmagnified.
Answer: (d)
Question 4. A cylindrical vessel containing a liquid is rotated about its axis so that the liquid rises at its sides as shown in the figure. The radius of vessel is 5 cm an and the angular speed of rotation is
a)
b)
c)
d)
\(\begin{array}{l}\omega\end{array} \)
rad s–1. The difference in the height, h (in cm) of liquid at the centre of vessel and at the side will be:
a)
\(\begin{array}{l}\frac{5\omega ^{2}}{2g}\end{array} \)
b)
\(\begin{array}{l}\frac{2\omega ^{2}}{25g}\end{array} \)
c)
\(\begin{array}{l}\frac{25\omega ^{2}}{2g}\end{array} \)
d)
\(\begin{array}{l}\frac{2\omega ^{2}}{5g}\end{array} \)
\(\begin{array}{l}y=\frac{\omega ^{2}x^{2}}{2g}\end{array} \)
At x = 5cm , y =h
\(\begin{array}{l}h=\frac{\omega ^{2}5^{2}}{2g}=\frac{25\omega ^{2}}{2g}\end{array} \)
Answer: (c)
Question 5. If speed V, area A and force F are chosen as fundamental units, then the dimension of;
a) FA2V-3
b) FA2V-2
c) FA-1V0
d) FA2V-1
Young’s modulus will be
a) FA2V-3
b) FA2V-2
c) FA-1V0
d) FA2V-1
\(\begin{array}{l}y=k\left [ F \right ]^{x}\left [ A \right ]^{y}\left [ V \right ]^{z}\end{array} \)
\(\begin{array}{l}\left [ ML^{-1}T^{-2} \right ]=\left [ MLT^{-2} \right ]^{x}\left [ L^{2} \right ]^{y}\left [ LT^{-1} \right ]^{z}\end{array} \)
\(\begin{array}{l}\left [ ML^{-1}T^{-2} \right ]=\left [ M^{x}L^{x+2y+z} T^{-2x-z}\right ]\end{array} \)
x = 1, -2x-z = -2, x+2y+z = -1
z = 0
y = -1
Answer: (c)
Question 6. A bead of mass m stays at point P (a, b) on a wire bent in the shape of a parabola y = 4Cx2 and rotating with angular speed
a)
b)
c)
d)
\(\begin{array}{l}\omega\end{array} \)
(see figure). The value of \(\begin{array}{l}\omega\end{array} \)
is (neglect friction):
a)
\(\begin{array}{l}\sqrt{\frac{2g}{C}}\end{array} \)
b)
\(\begin{array}{l}2\sqrt{gC}\end{array} \)
c)
\(\begin{array}{l}\sqrt{\frac{2gC}{ab}}\end{array} \)
d)
\(\begin{array}{l}2\sqrt{2gC}\end{array} \)
Y = 4 cx2
(dy/dx) = 8cx
N cos θ = mg
N sin θ = mω2a
\(\begin{array}{l}tan\theta =\frac{m\omega ^{2}a}{mg}\end{array} \)
\(\begin{array}{l}tan\theta =\frac{m\omega ^{2}a}{mg}\end{array} \)
(x = a),
\(\begin{array}{l}8ca=\frac{\omega ^{2}a}{g}\end{array} \)
\(\begin{array}{l}2\sqrt{2gc}=\omega\end{array} \)
Answer: (d)
Question 7. Magnetic materials used for making permanent magnets (P) and magnets in a transformer (T) have different properties of the following, which property best matches for the type of magnet required?
a) P : Small retentivity, large coercivity
b) P : Large retentivity, large coercivity
c) T : Large retentivity, large coercivity
d) T : Large retentivity, small coercivity
a) P : Small retentivity, large coercivity
b) P : Large retentivity, large coercivity
c) T : Large retentivity, large coercivity
d) T : Large retentivity, small coercivity
Permanent magnet must retain for long use and should not be easily demagnetised
Answer: (b)
Question 8. Interference fringes are observed on a screen by illuminating two thin slits 1 mm apart with a light source (λ = 632.8 nm). The distance between the screen and the slits is 100cm. If a bright fringe is observed on screen at a distance of 1.27 mm from the central bright fringe, then the path difference between the waves, which are reaching this pointfrom the slits is close to:
a) 2.05 μ m
b) 2.87 nm
c) 2 nm
d) 1.27 μ m
a) 2.05 μ m
b) 2.87 nm
c) 2 nm
d) 1.27 μ m
given, d = 1mm
λ = 632.8 nm
D = 100cm
y = 1.27 mm
Δx =d sin θ
(θ = small)
Δx =d tan θ
\(\begin{array}{l}\Delta x=\frac{dy}{D}=\frac{1\times 10^{-3}\times 1.27\times 10^{-3}}{100\times 10^{-2}}\end{array} \)
= 1.27 × 10–6 m
= 1.27 μ m
Answer: (d)
Question 9. A gas mixture consists of 3 moles of oxygen and 5 moles of argon at temperature T. Assuming the gases to be ideal and the oxygen bond to be rigid, the total internal energy (in units of RT) of the mixture is:
a) 11
b) 13
c) 15
d) 20
a) 11
b) 13
c) 15
d) 20
U = n1Cv1T+ n2Cv2T
\(\begin{array}{l}U = 3 \times \frac{5}{2}RT+5\times \frac{3}{2}RT\end{array} \)
= (30/2)RT = 15RT
Answer: (c)
Question 10. A plane electromagnetic wave, has frequency of 2.0 × 1010 Hz and its energy density is 1.02 × 10–8 J/m3 in vacuum. The amplitude of the magnetic field of the wave is close
a) 160 nT
b) 150 nT
c) 180 nT
d) 190 nT
\(\begin{array}{l}(\frac{1}{4\pi \varepsilon _{0}}=9 \times 10^{9}\frac{Nm^{2}}{C^{2}})\end{array} \)
and speed of light = 3 x 108 m/sa) 160 nT
b) 150 nT
c) 180 nT
d) 190 nT
Energy density =
\(\begin{array}{l}\frac{B_{0}^{2}}{2\mu _{0}}\end{array} \)
———(1)
And
\(\begin{array}{l}C= \frac{1}{\sqrt{\mu _{0}\epsilon _{0}}}\end{array} \)
——–(2)
\(\begin{array}{l}\mu _{0}= \frac{1}{C^{2}\varepsilon _{0}}\end{array} \)
\(\begin{array}{l}B=\sqrt{U\times 2\mu _{0}}\end{array} \)
\(\begin{array}{l}B=\sqrt{1.02\times 10^{-8}\times 2\times \frac{1}{9\times 10^{16}}\times 4\pi \times 9\times 10^{9}}\end{array} \)
= 160nT
Answer: (a)
Question 11.Consider four conducting materials copper, tungsten, mercury and aluminium with resistivity ρc, ρm , ρT and ρA respectively. Then:
a) ρc > ρA> ρT
b) ρA> ρm > ρc
c) ρA> ρT > ρc
d) ρm > ρA> ρc
a) ρc > ρA> ρT
b) ρA> ρm > ρc
c) ρA> ρT > ρc
d) ρm > ρA> ρc
(Theoretical concept)
Answer: (d)
Question 12.A beam of protons with speed 4 x 105 ms–1 enters a uniform magnetic field of 0.3 T at an angle of 60° to the magnetic field. The pitch of the resulting helical path of protons is close to: (Mass of the pr oton =1.67 × 10–27 kg, charge of the proton =1.69 × 10–19C)
a) 4 cm
b) 2 cm
c) 12 cm
d) 5 cm
a) 4 cm
b) 2 cm
c) 12 cm
d) 5 cm
Pitch = Vcos 600 x T =
\(\begin{array}{l}\frac{V2\pi m}{2eB}\end{array} \)
\(\begin{array}{l}=4\times 10^{5}\times \frac{1}{2}\times \frac{2\pi }{0.3}\left ( \frac{m}{e} \right )\end{array} \)
\(\begin{array}{l}=\frac{4\pi \times 10^{5}\times 10^{-8}}{0.3}\end{array} \)
= 4cm
Answer: (a)
Question 13. Two identical strings X and Z made of same material have tension Tx and Tz in them. If their fundamental frequencies are 450 Hz and 300 Hz, respectively, then the ratio Tx/Tz is:
a) 2.25
b) 1.25
c) 0.44
d) 1.5
a) 2.25
b) 1.25
c) 0.44
d) 1.5
\(\begin{array}{l}f=\frac{1}{2L}\sqrt{\frac{T}{\mu }}\end{array} \)
given, μx = μz
& Lx = Ly as identical
F ∝
\(\begin{array}{l}\sqrt{T}\end{array} \)
Therefore,
\(\begin{array}{l}\frac{T_{x}}{T_{z}}=\frac{f_{x}^{2}}{f_{z}^{2}}=\left ( \frac{450}{300} \right )=\left ( \frac{3}{2} \right )^{2}=\frac{9}{4}\end{array} \)
\(\begin{array}{l}\frac{T_{x}}{T_{y}}=2.25\end{array} \)
Option (3) is the correct answer.
Answer: (a)
Question 14. A uniform cylinder of mass M and radius R is to be pulled over a step of height a(a < R) by applying a force F at its centre ‘O’ perpendicular to the plane through the axes of the cylinder on the edge of the step (see figure). The minimum value of F required is
(1) Mg√[(R/(R-a))2 – 1]
(2) Mg√(1 – a2/R2)
(3) Mga/R
(4) Mg√[1 – ((R-a)/R)2]
\(\begin{array}{l}cos\theta =\frac{\sqrt{R^{2}-(R-a)^{2}}}{R}\end{array} \)
\(\begin{array}{l}\sqrt{\frac{R^{2}}{R^{2}}-\left [ \frac{R-a}{R} \right ]^{2}}\end{array} \)
\(\begin{array}{l}\sqrt{1-\left [ \frac{R-a}{R} \right ]^{2}}\end{array} \)
To pull up, τF ≥τmg
FR ≥ mg cosθ R
for min F, Fmin = mg cos θ
\(\begin{array}{l}F_{min}=mg\sqrt{1-\left [ \frac{R-a}{R} \right ]^{2}}\end{array} \)
Answer: (d)
Question 15. In a reactor, 2 kg of 92U235 fuel is fully used up in 30 days. The energy released perfission is 200 MeV. Given that the Avogadro number, N = 6.023 × 1026per kilo mole and1 eV =1.6 × 10–19 J. The power output of the reactor is close to
a) 60 MW
b) 54 MW
c) 125 MW
d) 35 MW
a) 60 MW
b) 54 MW
c) 125 MW
d) 35 MW
\(\begin{array}{l}n(moles)=\frac{2kg}{235gm}=\frac{2000}{235}\end{array} \)
No. of nucleus = NA x n
= 6.022 x 1023 x (2000/235)
= 51. 25 x 1023
= 102.5 × 1025 MeV
= 102.5 × 1025 × 106 × 1.6 × 10–16J
= 164 × 106 MJ
\(\begin{array}{l}power \: = \: \frac{164 \times 10^{6}MJ}{30\times 24\times 60\times 60S}=0.063 \times 10^{3}MW\end{array} \)
= 60 MW
Answer: (a)
Question 16. A charged particle (mass m and charge q) moves along X axis with velocity V0. When it passes through the origin it enters a region having uniform electric field
a)
b)
c)
d)
\(\begin{array}{l}\vec{E}=-E\hat{j}\end{array} \)
which extends upto x = d. Equation of path of electron in the region x > d is :
a)
\(\begin{array}{l}y=\frac{qEd^{2}}{mV_{0}^{2}}x\end{array} \)
b)
\(\begin{array}{l}y=\frac{qEd}{mV_{0}^{2}}\left [ \frac{d}{2}-x \right ]\end{array} \)
c)
\(\begin{array}{l}y=\frac{qEd}{mV_{0}^{2}}\left [x-d\right ]\end{array} \)
d)
\(\begin{array}{l}y=\frac{qEd}{mV_{0}^{2}}x\end{array} \)
\(\begin{array}{l}-y=\frac{1}{2}at^{2}\end{array} \)
\(\begin{array}{l}-y=\frac{1}{2}\frac{qE}{m}t^{2}\end{array} \)
——–(1)
X = V0t
t=x/ V0 ——(2)
for x ≤d,
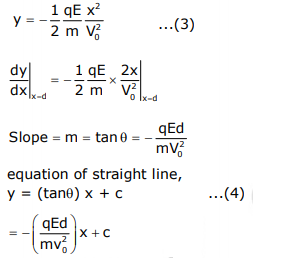
(now for C, at x = d,
\(\begin{array}{l}y=\frac{qEd^{2}}{2mv_{0}^{2}}\end{array} \)
put in (4)
\(\begin{array}{l}-\frac{qEd^{2}}{2mv_{0}^{2}}=\frac{qEd^{2}}{mv_{0}^{2}}+C\end{array} \)
\(\begin{array}{l}C=\frac{qEd^{2}}{2mv_{0}^{2}}\end{array} \)
For x > d,
\(\begin{array}{l}y=-\left [ \frac{qEd}{mV_{0}^{2}} \right ]x+\frac{qEd^{2}}{2mv_{0}^{2}}\end{array} \)
\(\begin{array}{l}y=\left [ \frac{qEd}{mV_{0}^{2}} \right ]\left ( \frac{d}{2}-x \right )\end{array} \)
Answer: (b)
Question 17. Train A and train B are running on parallel tracks in the opposite directions with speeds of 36 km/hour and 72 km/hour, respectively. A person is walking in train A in the direction opposite to its motion with a speed of 1.8 km/hour. Speed (in ms–1) of this person as observed from train B will be close to:
a) 29.5 ms–1
b) 30.5 ms–1
c) 31.5 ms–1
d) 28.5 ms–1
a) 29.5 ms–1
b) 30.5 ms–1
c) 31.5 ms–1
d) 28.5 ms–1
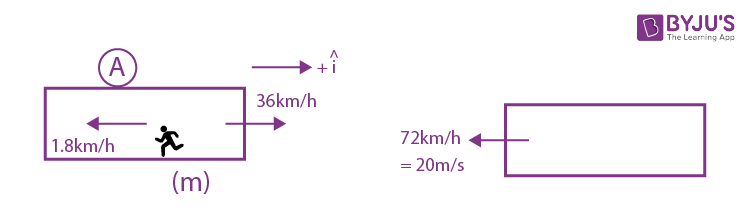
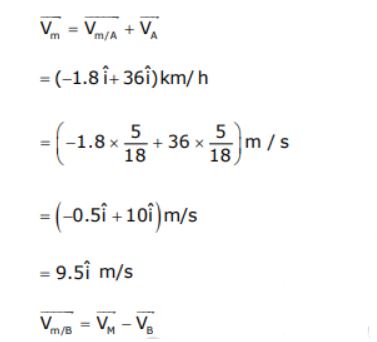
\(\begin{array}{l}= 9.5\hat{i}-(-20\hat{i})m/s\end{array} \)
=
\(\begin{array}{l}= 29.5m/s\hat{i}\end{array} \)
Answer (a)
Question 18. Shown in the figure is rigid and uniform one meter long rod AB held in horizontal position by two strings tied to its ends and attached to the ceiling. The rod is of mass `m` and has another weight of mass 2 m hung at a distance of 75 cm from A. The tension in the string at A is:
a) 0.75 mg
b) 0.5 mg
c) 1 mg
d) 2 mg
a) 0.75 mg
b) 0.5 mg
c) 1 mg
d) 2 mg
At equilibrium torque about any axis must be zero. Taking the torque about B.
T × 100cm = mg × 50cm + 2mg × 25cm
T = 1 mg
Answer (c)
Question 19.The least count of the main scale of a vernier callipers is 1 mm. Its vernier scale is divided into 10 divisions and coincide with 9 divisions of the main scale. When jaws are touching each other, the 7th division of vernier scale coincides with a division of main scale and the zero of vernier scale is lying right side of the zero of main scale. When this vernier is used to measure length of a cylinder the zero of the vernier scale between 3.1 cm and 3.2 cm and 4th VSD coincides with a main scale division. The length of the cylinder is: (VSD is vernier scale division)
a) 3.21 cm
b) 3.07 cm
c) 2.99 cm
d) 3.2 cm
a) 3.21 cm
b) 3.07 cm
c) 2.99 cm
d) 3.2 cm
L.C. = 1MSD – 1VSD
L.C. = 0.1MSD
1 MSD = 1mm
L. C. = 0.1mm
+ve zero error = +7 × L.C. = 0.7mm
Reading = (3.1cm + 4 × L.C) – zero error
= 3.1cm + 0.4mm – 0.7mm
= 3.1cm – 0.03cm (as given 1 MSD = 1mm)
= 3.07 cm
Answer: (b)
Question 20. A particle of mass m with an initial velocity
a)
b)
c)
d)
\(\begin{array}{l}u\hat{i}\end{array} \)
collides perfectly elastically with a mass 3m at rest. It moves with a velocity \(\begin{array}{l}u\hat{j}\end{array} \)
after collision, then v is given by:a)
\(\begin{array}{l}v=\frac{1}{\sqrt{6}}u\end{array} \)
b)
\(\begin{array}{l}v=\sqrt{\frac{2}{3}u}\end{array} \)
c)
\(\begin{array}{l}v=\frac{u}{\sqrt{3}}\end{array} \)
d)
\(\begin{array}{l}v=\frac{u}{\sqrt{2}}\end{array} \)
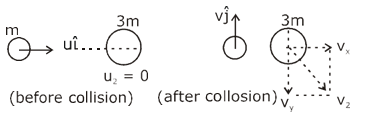
Answer: (d)
Question 21. A small block starts slipping down from a point B on an inclined plane AB, which is making an angle θ with the horizontal section BC is smooth and the remaining section CA is rough with a coefficient of friction. It is found that the block comes to rest as it reaches the bottom (point A) of the inclined plane. If BC = 2AC, the coefficient of friction is given by μ =k tan θ. The value of k is __________
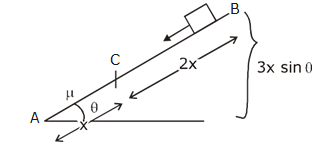
from work energy theorem
Wg + Wr = ΔKE
Mg3 x sin θ- μmgcos θ x = 0 -0
3tan θ = μ
K= 3
Answer: (3)
Question 22.An engine takes in 5 moles of air at 20°C and 1atm, and compresses it adiabaticaly to 1/10th of the original volume. Assuming air to be a diatomic ideal gas made up of rigid molecules, the change in its internal energy during this process comes out to be X kJ. The value of X to the nearest integer is ___________.
Answer: (46kJ)
Question 23. When radiation of wavelength λ is used to illuminate a metallic surface, the stopping potential is V. When the same surface is illuminated with radiation of wavelength 3 λ, the stopping potential is V/4. If the threshold wavelength for the metallic surface is n λ then value of n will be __________.
\(\begin{array}{l}\frac{hc}{\lambda }=\phi + eV\end{array} \)
——-(1)
\(\begin{array}{l}\frac{hc}{3\lambda }=\phi + \frac{eV}{4}\end{array} \)
———-(2)
Equ (1)/equa(2)
\(\begin{array}{l}3 = \frac{\phi +eV}{\phi +\frac{eV}{4}}\end{array} \)
\(\begin{array}{l}3\phi +\frac{3eV}{4} = \phi +eV\end{array} \)
\(\begin{array}{l}\phi = \frac{eV}{8}\end{array} \)
\(\begin{array}{l}\frac{hc}{\lambda } = \frac{eV}{8}+eV = \frac{9}{8}eV\end{array} \)
Therefore,
\(\begin{array}{l}ev = \frac{8}{9}\frac{hc}{\lambda }\end{array} \)
So,
\(\begin{array}{l}\phi -\frac{hc}{\lambda } = \frac{8}{9}\frac{hc}{\lambda }\end{array} \)
\(\begin{array}{l}\phi = \frac{1}{9}\frac{hc}{\lambda }\end{array} \)
\(\begin{array}{l}\frac{hc}{\lambda _{th}} = \frac{hc}{9\lambda }\end{array} \)
\(\begin{array}{l}\lambda _{th}=9\lambda\end{array} \)
Answer: (9λ)
Question 24.A circular coil of radius 10 cm is placed in uniform magnetic field of 3.0 × 10–5 T with its plane perpendicular to the field initially. It is rotated at constant angular speed about an axis along the diameter of coil and perpendicular to magnetic field so that it undergoes half of rotation in 0.2s. The maximum value of EMF induced (in μV) in the coil will be close to the integer __________.
\(\begin{array}{l}\phi =BAcos\omega t\end{array} \)
\(\begin{array}{l}E=\frac{-d\phi }{dt}=BA\omega sin\omega t\end{array} \)
\(\begin{array}{l}E_{m}=BA\omega\end{array} \)
(ω= π/0.2)
= 3 x 10-5 x πR2 x (π/0.2)
= 15 x 10-6 V
= 15 μV
Answer: (15 μV)
Question 25. A 5μF capacitor is charged fully by a 220V supply. It is then disconnected from the supply and is connected in series to another uncharged 2.5μ F capacitor. If the energy change during the charge redistribution is (X/100) J then value of X to the nearest integer is _________.
*NTA Answer is 36
Heat = Ui – Uf
\(\begin{array}{l}=\frac{1}{2}\frac{C_{1}C_{2}}{C_{1}+C_{2}}(V_{1}-V_{2})^{2}\end{array} \)
\(\begin{array}{l}=\frac{1}{2}\frac{5\times 2.5}{7.5}(220-0)^{2}\mu J\end{array} \)
\(\begin{array}{l}=\frac{5}{6}\times 220\times 220\times 10^{-6}J\end{array} \)
= 40,333.33 x 10-6J
= 40.3 × 10-3 =(X/100)
⇒ x = 4.03
≈ 4
Answer (4)
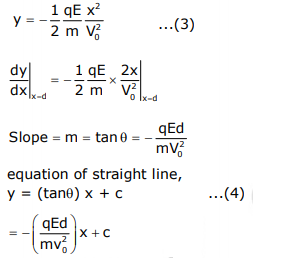
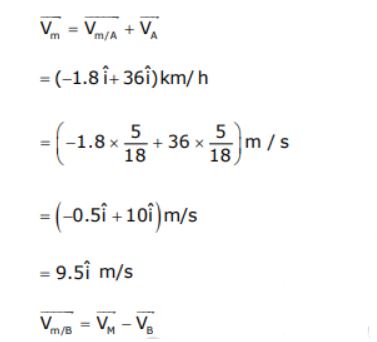
Comments