The JEE Main 2022 July 28 – Shift 2 Maths Question Paper with Solutions is given on this page. JEE Main 2022 answer keys can be used to assess your performance and calculate the expected scores. Students can use the JEE Main 2022 question paper with solutions for revision and thus make their knowledge in each subject more thoroughly. Solving the JEE Main 2022 question papers is an effective way to prepare for JEE exams. Solve and practise the JEE Main 2022 July 28 – Shift 2 Maths Question Paper with Solutions given below.
JEE Main 2022 July 28th Shift 2 Mathematics Question Paper and Solutions
SECTION – A
Multiple Choice Questions: This section contains 20 multiple choice questions. Each question has 4 choices (1), (2), (3) and (4), out of which ONLY ONE is correct.
Choose the correct answer :
1. Let \(\begin{array}{l} S=\left\{x\in\left[-6, 3\right]-\left\{-2,2 \right\}:\frac{\left|x+3\right|-1}{\left|x\right|-2}\geq 0 \right\}\ \text{and} T=\left\{x\in \mathbb{Z}:x^2-7\left|x\right|+9\leq 0\right\}.\end{array} \)
Then the number of elements in S ⋂ T is
(A) 7
(B) 5
(C) 4
(D) 3
Answer (D)
Sol.
\(\begin{array}{l} \left|x\right|^2-7\left|x\right|+9\leq0\end{array} \)
\(\begin{array}{l} \Rightarrow \left|x\right|\in \left[\frac{7-\sqrt{13}}{2},\frac{7+\sqrt{13}}{2}\right] \end{array} \)
\(\begin{array}{l}\text{As}~ x \in Z\end{array} \)
\(\begin{array}{l}\text{So, x can be} \pm 2, \pm 3, \pm 4, \pm 5\end{array} \)
Out of these values of x,
x = 3, –4, –5
satisfy S as well
\(\begin{array}{l}n\left(S\cap T \right) = 3\end{array} \)
2. Let α, β be the roots of the equation \(\begin{array}{l} x^2-\sqrt{2}x+\sqrt{6}=0\ \text{and}\ \frac{1}{\alpha^2}+1,\frac{1}{\beta^2}+1\end{array} \)
be the roots of the equation x2 + ax + b = 0 . Then the roots of the equation x2 – (a + b – 2)x + (a + b + 2) = 0 are
(A) Non-real complex number
(B) Real and both negative
(C) Real and both positive
(D) Real and exactly one of them is positive
Answer (B)
Sol.
\(\begin{array}{l} \alpha+\beta=\sqrt{2},\alpha\beta=\sqrt{6}\end{array} \)
\(\begin{array}{l} \frac{1}{\alpha^2}+1+\frac{1}{\beta^2}+1=2+\frac{\alpha^2+\beta^2}{6} \end{array} \)
\(\begin{array}{l} =2+\frac{2-2\sqrt{6}}{6}=-a \end{array} \)
\(\begin{array}{l} \left(\frac{1}{\alpha^2}+1\right)\left(\frac{1}{\beta^2}+1\right)=1+\frac{1}{\alpha^2}+\frac{1}{\beta^2}+\frac{1}{\alpha^2\beta^2}\end{array} \)
\(\begin{array}{l} =\frac{7}{6}+\frac{2-2\sqrt{6}}{6}=b\end{array} \)
\(\begin{array}{l} \Rightarrow a+b=\frac{-5}{6}\end{array} \)
So, equation is
\(\begin{array}{l} x^2+\frac{17x}{6}+\frac{7}{6}=0\end{array} \)
Or 6x2 + 17x + 7 = 0
Both roots of the equation are –ve and distinct.
3. Let A and B be any two 3 × 3 symmetric and skew symmetric matrices, respectively. Then Which of the following is NOT true?
(A) A4 – B4 is a symmetric matrix
(B) AB – BA is a symmetric matrix
(C) B5 – A5 is a skew-symmetric matrix
(D) AB + BA is a skew-symmetric matrix
Answer (C)
Sol.
\(\begin{array}{l}\left(A\right) M = A^4 – B^4\\ M^T = \left(A^4 – B^4\right)^T = \left(A^T\right)^4 – \left(B^T\right)^4\\ = A^4 – \left(-B\right)^4 = A^4 – B^4 = M\end{array} \)
\(\begin{array}{l}\left(B\right) M = AB – BA\\ M^T = \left(AB – BA\right)^T = \left(AB\right)^T – \left(BA\right)^T\\ = B^TA^T – A^TB^T\\ = -BA – A\left(-B\right)\\ = AB – BA = M\end{array} \)
\(\begin{array}{l}\left(C\right) M = B^5 – A^5\\ M^T = \left(B^T\right)^5 – \left(A^T\right)^5 = -\left(B^5 + A^5\right) \ne -M \end{array} \)
\(\begin{array}{l}\left(D\right) M = AB + BA\\ M^T = \left(AB\right)^T + \left(BA\right)^T\\ = B^TA^T + A^TB^T= -BA – AB = -M\end{array} \)
4. Let f(x) = ax2 + bx + c be such that f(1) = 3, f(-2) = λ and f(3) = 4. If f(0) + f(1) + f(-2) + f(3) = 14, then λ is equal to
\(\begin{array}{l}\left(A\right) -4\\ \left(B\right) \frac{13}{2} \\ \left(C\right)\frac{23}{2}\\ \left(D\right)4\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l}f\left(1\right) = a + b + c = 3\cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot \left(i\right)\\ f\left(3\right) = 9a + 3b + c = 4 \cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot\left(ii\right)\end{array} \)
\(\begin{array}{l}f\left(0\right) + f\left(1\right) + f\left(-2\right) + f\left(3\right) = 14\\ \text{OR}~ c + 3 + \left(4a -2b + c\right) + 4 = 14\end{array} \)
\(\begin{array}{l}\text{OR}~ 4a – 2b + 2c = 7\cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot \left(iii\right)\\ \text{From}~ \left(i\right) ~\text{and}~ \left(ii\right) 8a + 2b = 1 \cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot\left(iv\right)\end{array} \)
\(\begin{array}{l}From \left(iii\right) – \left(2\right) \times \left(i\right)\\ \Rightarrow 2a – 4b = 1\cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot\cdot\left(v\right)\end{array} \)
\(\begin{array}{l}\text{From} \left(iv\right) \text{and} \left(v\right) a=\frac{1}{6},b=\frac{-1}{6}\text{ and }c= 3\end{array} \)
\(\begin{array}{l} f\left(-2\right) = 4a – 2b + c\end{array} \)
\(\begin{array}{l} =\frac{4}{6}+\frac{2}{6}+3=4\end{array} \)
5. The function f: ℝ → ℝ defined by \(\begin{array}{l} f\left(x\right)=\displaystyle \lim_{n \to \infty}\frac{\cos\left(2\pi x\right)-x^{2n}\sin\left(x-1\right)}{1+x^{2n+1}-x^{2n}}\end{array} \)
is continuous for all x in
\(\begin{array}{l} (\text{A})\ \mathbb{R} – \left\{-1 \right\}\end{array} \)
\(\begin{array}{l} (\text{B})\ \mathbb{R} – \left\{-1,1 \right\}\end{array} \)
\(\begin{array}{l} (\text{C})\ \mathbb{R} – \left\{1 \right\}\end{array} \)
\(\begin{array}{l} (\text{D})\ \mathbb{R} – \left\{0 \right\}\end{array} \)
Answer (B)
Sol.
\(\begin{array}{l} f\left(x\right)=\displaystyle \lim_{n \to \infty}\frac{\cos\left(2\pi x\right)-x^{2n}\sin\left(x-1\right)}{1+x^{2n+1}-x^{2n}}\end{array} \)
\(\begin{array}{l}\text{For} \left|x\right| < 1, f\left(x\right) = cos2\pi x, \text{continuous function}\end{array} \)
|x| > 1,
\(\begin{array}{l} f\left(x\right)=\displaystyle \lim_{n \to \infty}\frac{x^{\frac{1}{{2n}}\cos2\pi x-\sin\left(x-1\right)}}{x^{\frac{1}{2n}+x-1}}\end{array} \)
\(\begin{array}{l} =\frac{-\sin\left(x-1\right)}{x-1},\text{continuous}\end{array} \)
For |x| = 1,
\(\begin{array}{l} f\left(x\right)=\left\{\begin{matrix}1 & \text{if}&x=1 \\-1\left(1+\sin2\right)&\text{if} &x=-1 \\\end{matrix}\right. \end{array} \)
Now,
\(\begin{array}{l} \displaystyle \lim_{x \to 1^+} f\left(x\right)=-1,~~~\displaystyle \lim_{x \to 1^-}f\left(x\right)=1,\end{array} \)
so discontinuous at x = 1
\(\begin{array}{l} \displaystyle \lim_{x \to -1^+}f\left(x\right)=1,~~\displaystyle \lim_{x \to -1^-}f\left(x\right)=-\frac{\sin2}{2},\end{array} \)
so discontinuous at x = –1
\(\begin{array}{l} \therefore f\left(x\right)\text{is continuous for all}~ x \in R – \{-1, 1\}\end{array} \)
6. The function \(\begin{array}{l} f\left(x\right)=xe^{x\left(1-x\right)}, x\in \mathbb{R} \end{array} \)
is
\(\begin{array}{l} (\text{A})\ \text{Increasing in}\left(-\frac{1}{2},1\right)\end{array} \)
\(\begin{array}{l} (\text{B})\ \text{Decreasing in}\left(\frac{1}{2},2\right)\end{array} \)
\(\begin{array}{l} (\text{C})\ \text{Increasing in}\left(-1,-\frac{1}{2}\right)\end{array} \)
\(\begin{array}{l} (\text{D})\ \text{Decreasing in}\left(-\frac{1}{2},\frac{1}{2}\right)\end{array} \)
Answer (A)
Sol.
\(\begin{array}{l} f\left(x\right)=xe^{x\left(1-x\right)},x\in \mathbb{R}\end{array} \)
\(\begin{array}{l} f’\left(x\right)=xe^{x\left(1-x\right)}.\left(1-2x\right)+e^{x\left(1-x\right)}\end{array} \)
\(\begin{array}{l} =e^{x\left(1-x\right)}\left[x-2x^2+1\right]\end{array} \)
\(\begin{array}{l} =-e^{x\left(1-x\right)}\left[2x^2-x-1\right] \end{array} \)
\(\begin{array}{l} =-e^{x\left(1-x\right)}\left(2x+1\right)\left(x-1\right)\end{array} \)
∴ f(x) is increasing in
\(\begin{array}{l} \left(-\frac{1}{2},1\right) \end{array} \)
and decreasing in \(\begin{array}{l} \left(-\infty, -\frac{1}{2}\right)\cup \left(1,\infty\right)\end{array} \)
7. The sum of the absolute maximum and absolute minimum values of the function \(\begin{array}{l} f\left(x\right)=\tan^{-1}\left(\sin x-\cos x\right) \end{array} \)
in the interval [0, π] is
\(\begin{array}{l} (\text{A}) 0\end{array} \)
\(\begin{array}{l} (\text{B})\ \tan^{-1}\left(\frac{1}{\sqrt{2}}\right)-\frac{\pi}{4}\end{array} \)
\(\begin{array}{l} (\text{C})\ \cos^{-1}\left(\frac{1}{\sqrt{3}}\right)-\frac{\pi}{4}\end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{-\pi}{12}\end{array} \)
Answer (C)
Sol.
\(\begin{array}{l} f\left(x\right)=\tan^{-1}\left(\sin x-\cos x\right),~~\left[0,\pi\right]\end{array} \)
Let
\(\begin{array}{l} g\left(x\right)=\sin x-\cos x \end{array} \)
\(\begin{array}{l} =\sqrt{2}\sin\left(x-\frac{\pi}{4}\right)\text{ and }x-\frac{\pi}{4}\in \left[\frac{-\pi}{4},\frac{3\pi}{4}\right]\end{array} \)
\(\begin{array}{l} \therefore g\left(x\right)\in\left[-1,\sqrt{2}\right] \end{array} \)
and tan-1 x is an increasing function
\(\begin{array}{l} \therefore\ f\left(x\right)\in \left[\tan^{-1}\left(-1\right),\tan^{-1}\sqrt{2}\right]\end{array} \)
\(\begin{array}{l} \in\left[-\frac{\pi}{4},\tan^{-1}\sqrt{2}\right] \end{array} \)
\(\begin{array}{l}\therefore~\text{Sum of} ~f_{\text{max}}\text{ and }f_{\text{min}}=\tan^{-1}\sqrt{2}-\frac{\pi}{4}\end{array} \)
\(\begin{array}{l} =\cos^{-1}\left(\frac{1}{\sqrt{3}}\right)-\frac{\pi}{4} \end{array} \)
8. Let \(\begin{array}{l} x\left(t\right)=2\sqrt{2}\cos t\sqrt{\sin 2t}\ \text{and}\ y\left(t\right)=2\sqrt{2}\sin t\sqrt{\sin 2t},t\in \left(0,\frac{\pi}{2}\right).\end{array} \)
\(\begin{array}{l}\text{Then}\ \frac{1+\left(\frac{dy}{dx}\right)^2}{\frac{d^2y}{dx^2}}\ \text{at}\ t=\frac{\pi}{4}\end{array} \)
is equal to
\(\begin{array}{l} (\text{A})\ \frac{-2\sqrt{2}}{3}\end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{2}{3}\end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{1}{3}\end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{-2}{3}\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l} x=2\sqrt{2}\cos t\sqrt{\sin2t} , y=2\sqrt{2}\sin t\sqrt{\sin 2t}\end{array} \)
\(\begin{array}{l} \therefore\ \frac{dx}{dt}=\frac{2\sqrt{2}\cos 3t}{\sqrt{\sin 2t}}, \frac{dy}{dt}=\frac{2\sqrt{2}\sin 3t}{\sqrt{\sin2t}}\end{array} \)
\(\begin{array}{l} \therefore\ \frac{dy}{dx}=\tan 3t, \left(\text{at }t=\frac{\pi}{4},\frac{dy}{dx}=-1\right) \end{array} \)
and
\(\begin{array}{l} \frac{d^2y}{dx^2}=3\sec^23t\cdot\frac{dt}{dx}=\frac{3\sec^23t\cdot\sqrt{\sin2t}}{2\sqrt{2}\cos3t}\end{array} \)
\(\begin{array}{l} \left(\text{At }t=\frac{\pi}{4},\frac{d^2y}{dx^2}=-3\right)\end{array} \)
\(\begin{array}{l} \therefore \frac{1+\left(\frac{dy}{dx}\right)^2}{\frac{d^2y}{dx^2}}=\frac{2}{-3}=\frac{-2}{3}\end{array} \)
9. Let \(\begin{array}{l} I_n\left(x\right)=\int_0^x\frac{1}{\left(t^2+5\right)^n}dt, n=1, 2, 3,\cdots\end{array} \)
Then
\(\begin{array}{l} (\text{A})\ 50I_6-9I_5=x\overset{‘}{I}_5 \end{array} \)
\(\begin{array}{l} (\text{B})\ 50I_6-11I_5=x\overset{‘}{I}_5 \end{array} \)
\(\begin{array}{l} (\text{C})\ 50I_6-9I_5=\overset{‘}{I}_5 \end{array} \)
\(\begin{array}{l} (\text{D})\ 50I_6-11I_5=\overset{‘}{I}_5 \end{array} \)
Answer (A)
Sol.
\(\begin{array}{l} I_n\left(x\right)=\displaystyle\int\limits_0^x\frac{1}{\left(t^2+5\right)^n}dt\end{array} \)
\(\begin{array}{l} =\displaystyle\int\limits_0^x\frac{1}{\underset{I}{\underbrace{\left(t^2+5\right)^n}}}\times\underset{II}{\underbrace{I}}dt\end{array} \)
\(\begin{array}{l} \left.=\frac{t}{\left(t^2+5\right)^n} \right|^x_0-\displaystyle\int\limits_0^x\frac{-2nt}{\left(t^2+5\right)^{n+1}}\times t\ dt\end{array} \)
\(\begin{array}{l} =\frac{x}{\left(x^2+5\right)^n}+\displaystyle\int\limits_0^x2n\left(\frac{t^2+5-5}{\left(t^2+5\right)^{n+1}}\right)dt\end{array} \)
\(\begin{array}{l} I_n\left(x\right)=\frac{x}{\left(x^2+5\right)^n}+2n\ I_n\left(x\right)-10n\ I_{n+1}\left(x\right) \end{array} \)
\(\begin{array}{l} 10n\ I_{n+1}\left(x\right)-\left(2n-1\right)\ I_n\left(x\right)=xI’_n\left(x\right) \end{array} \)
\(\begin{array}{l} \text{For}~n=5\\50I_6\left(x\right)-9I_5\left(x\right)=xI’_5\left(x\right)\end{array} \)
10. The area enclosed by the curves \(\begin{array}{l} y=\text{log}_e\left(x+e^2\right),\ x=\text{log}_e\left(\frac{2}{y}\right)\text{ and }x=\text{ log }_e\ 2,\end{array} \)
above the line y = 1 is
\(\begin{array}{l} \left(A\right) 2 + e – log_e2 \\\left(B\right) 1 + e – log_e2\\ \left(C\right) e – log_e2 \\\left(D\right) 1 + log_e2\end{array} \)
Answer (B*)
Sol.
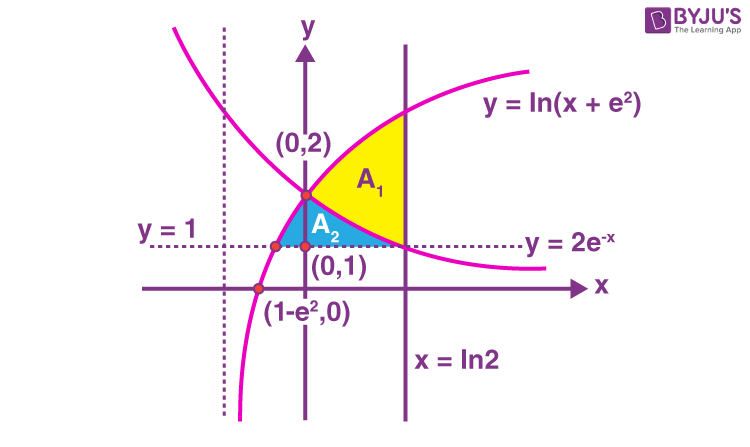
According to NTA, the required region A2, which is shaded in crossed lines and comes out to be
\(\begin{array}{l} A_2=\displaystyle\int\limits_1^2\left(\text{In }\frac{2}{y}-e^y+e^2\right)dy=1+e-\text{In}2 \end{array} \)
But according to us the required region A1 comes out to be shaded in parallel lines, which can be obtained as
\(\begin{array}{l} A_1=\displaystyle\int\limits_0^{\text{In }2}\left(\text{In}\left(x+e^2\right)-2e^{-x}\right)dx\end{array} \)
\(\begin{array}{l} \left. =\left\{\left(x+e^2\right)\text{In}\left(x+e^2\right)-x+2e^{-x} \right\} \right|_0^{\text{In }2}\end{array} \)
\(\begin{array}{l} =\left(\text{In}2+e^2\right)\text{In}\left(\text{In2}+e^2\right)-\text{In}2+1-2e^2 – 2\end{array} \)
\(\begin{array}{l} =\left(\text{In}2+e^2\right)\text{In}\left(\text{In}2-e^2\right)-\text{In}2-2e^2-1\end{array} \)
Not given in any option.
The region asked in the question is bounded by three curves
\(\begin{array}{l} y=\text{In}\left(x+e^2\right)\end{array} \)
\(\begin{array}{l} x=\text{In}\left(\frac{2}{y}\right) \end{array} \)
\(\begin{array}{l} x=\text{In}2\end{array} \)
There is only one region which satisfies above requirement and which also lies above line y = 1
Line y = 1 may or may not be the boundary of the region.
11. Let y = y(x) be the solution curve of the differential equation \(\begin{array}{l} \frac{dy}{dx}+\frac{1}{x^2-1}y=\left(\frac{x-1}{x+1}\right)^{1/2},x>1 \end{array} \)
passing through the point (2, √ (1/3)). Then √ 7 y(8) is
\(\begin{array}{l} \left(A\right) 11 + 6 log_e3\\ \left(B\right) 19\\ \left(C\right) 12 – 2 log_e3\\ \left(D\right) 19 – 6 log_e3\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l} \frac{dy}{dx}+\frac{1}{x^2-1}y=\sqrt{\frac{x-1}{x+1}},x>1\end{array} \)
Integrating factor
\(\begin{array}{l} \text{I.F.}=e^{\int\frac{1}{x^2-1}dx}=e^{\frac{1}{2}\text{In}\left|\frac{x-1}{x+1}\right|} \end{array} \)
\(\begin{array}{l} =\sqrt{\frac{x-1}{x+1}}\end{array} \)
Solution of differential equation
\(\begin{array}{l} y\sqrt{\frac{x-1}{x+1}}=\int\frac{x-1}{x+1}dx =\int\left(1-\frac{2}{x+1}\right)dx\end{array} \)
\(\begin{array}{l} y\sqrt{\frac{x-1}{x+1}}=x-2\text{In}\left|x+1\right|+C\end{array} \)
Curve passes through (2, √ (1/3) )
\(\begin{array}{l} \frac{1}{\sqrt{3}}\times\frac{1}{\sqrt{3}}=2-2\text{In}3+C \end{array} \)
\(\begin{array}{l} C=2\text{In}3-\frac{5}{3} \end{array} \)
\(\begin{array}{l} y\left(8\right)\times\frac{\sqrt{7}}{3}=8-2\text{In}9+2\text{In}3-\frac{5}{3}\end{array} \)
\(\begin{array}{l} \sqrt{7}\cdot y\left(8\right)=19-6\text{In}3 \end{array} \)
12. The differential equation of the family of circles passing through the points (0, 2) and (0, –2) is
\(\begin{array}{l} (\text{A})\ 2xy\frac{dy}{dx}+\left(x^2-y^2+4\right)=0 \end{array} \)
\(\begin{array}{l} (\text{B})\ 2xy\frac{dy}{dx}+\left(x^2+y^2-4\right)=0\end{array} \)
\(\begin{array}{l} (\text{C})\ 2xy\frac{dy}{dx}+\left(y^2-x^2+4\right)=0\end{array} \)
\(\begin{array}{l} (\text{D})\ 2xy\frac{dy}{dx}-\left(x^2-y^2+4\right)=0\end{array} \)
Answer (A)
Sol. Family of circles passing through the points (0, 2) and (0, –2)
\(\begin{array}{l}x^2 + \left(y – 2\right) \left(y + 2\right) + \lambda x = 0, \lambda \in \mathbb{R}\\ x^2 + y^2 + \lambda x – 4 = 0 \cdot\cdot\cdot\cdot\cdot\cdot\left(1\right)\end{array} \)
Differentiate w.r.t x
\(\begin{array}{l} 2x+2y\frac{dy}{dx}+\lambda=0\cdots\left(2\right)\end{array} \)
Using (1) and (2), eliminate λ
\(\begin{array}{l} x^2+y^2-\left(2x+2y\frac{dy}{dx}\right)x-4=0\end{array} \)
\(\begin{array}{l} 2xy\frac{dy}{dx}+x^2-y^2+4=0\end{array} \)
13. Let the tangents at two points A and B on the circle x2 + y2 – 4x + 3 = 0 meet at origin O(0, 0). Then the area of the triangle OAB is
\(\begin{array}{l} (\text{A})\ \frac{3\sqrt{3}}{2} \end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{3\sqrt{3}}{4} \end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{3}{2\sqrt{3}} \end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{3}{4\sqrt{3}}\end{array} \)
Answer (B)
Sol.
\(\begin{array}{l}x^2 + y^2 – 4x + 3 = 0\end{array} \)
\(\begin{array}{l} \Rightarrow \left(x-2\right)^2+y^2=1 \end{array} \)
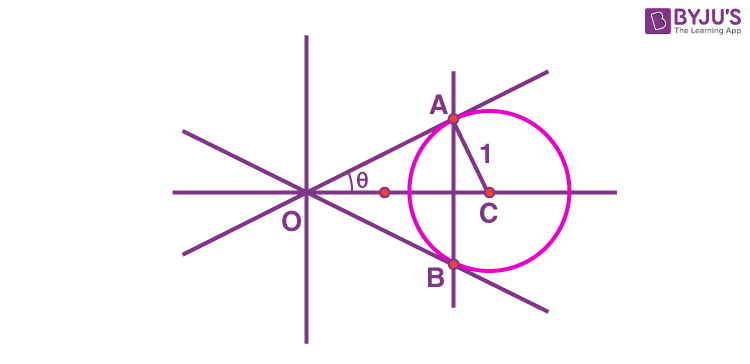
\(\begin{array}{l} AO=\sqrt{\left(OC\right)^2-\left(AC\right)^2} \end{array} \)
\(\begin{array}{l} =\sqrt{4-1}=\sqrt{3}\end{array} \)
\(\begin{array}{l} \sin\theta=\frac{1}{2}\Rightarrow\theta=\frac{\pi}{6}\end{array} \)
Also, AO = BO
\(\begin{array}{l} \text{Area of }\Delta OAB=\frac{1}{2}\cdot OA\cdot OB \sin60^\circ \end{array} \)
\(\begin{array}{l} =\frac{1}{2}\times \sqrt{3}\cdot\sqrt{3}\cdot \frac{\sqrt{3}}{2}=\frac{3\sqrt{3}}{4}\end{array} \)
14. Let the hyperbola \(\begin{array}{l} H:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\ \text{pass through the point}\ \left(2\sqrt{2},-2\sqrt{2}\right).\end{array} \)
A parabola is drawn whose focus is same as the focus of H with positive abscissa and the directrix of the parabola passes through the other focus of H. If the length of the latus rectum of the parabola is e times the length of the latus rectum of H, where e is the eccentricity of H, then which of the following points lies on the parabola?
\(\begin{array}{l} (\text{A})\ \left(2\sqrt{3},3\sqrt{2}\right)\end{array} \)
\(\begin{array}{l} (\text{B})\ \left(3\sqrt{3},-6\sqrt{2}\right)\end{array} \)
\(\begin{array}{l} (\text{C})\ \left(\sqrt{3},-\sqrt{6}\right)\end{array} \)
\(\begin{array}{l} (\text{D})\ \left(3\sqrt{6},6\sqrt{2}\right)\end{array} \)
Answer (B)
Sol.
\(\begin{array}{l} H:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1 \end{array} \)
Focus of parabola: (ae, 0)
Directrix: x = – ae.
Equation of parabola ≡y2 = 4aex
Length of latus rectum of parabola = 4ae
\(\begin{array}{l}\text{Length of latus rectum of hyperbola} =\frac{2\cdot b^2}{a} \end{array} \)
as given,
\(\begin{array}{l} 4ae=\frac{2b^2}{a}\cdot e\end{array} \)
\(\begin{array}{l} 2=\frac{b^2}{a^2}\cdots \left(i\right)\end{array} \)
\(\begin{array}{l} \because \text{H passes through} \left(2\sqrt{2},-2\sqrt{2}\right)\Rightarrow \frac{8}{a^2}-\frac{8}{b^2}=1\cdots \left(ii\right)\end{array} \)
From (i) and (ii) a2 = 4 and b2 = 8
\(\begin{array}{l}\Rightarrow e=\sqrt{3}\end{array} \)
\(\begin{array}{l} \Rightarrow\text{Equation of parabola is}~ y^2=8\sqrt{3}x\end{array} \)
15. Let the lines \(\begin{array}{l} \frac{x-1}{\lambda}=\frac{y-2}{1}=\frac{z-3}{2}\ \text{and}\ \frac{x+26}{-2}=\frac{y+18}{3}=\frac{z+28}{\lambda}\end{array} \)
be coplanar and P be the plane containing these two lines. Then which of the following points does NOT lie on P?
(A) (0, -2, -2)
(B) (-5, 0, -1)
(C) (3, -1, 0)
(D) (0, 4, 5)
Answer (D)
Sol.
\(\begin{array}{l} L_1:\frac{x-1}{\lambda}=\frac{y-2}{1}=\frac{z-3}{2},\end{array} \)
through a point
\(\begin{array}{l} \overrightarrow{a}_1\equiv \left(1, 2, 3\right)\end{array} \)
parallel to
\(\begin{array}{l} \overrightarrow{b}_1\equiv \left(\lambda, 1, 2\right)\end{array} \)
\(\begin{array}{l} L_2:\frac{x+26}{-2}=\frac{y+18}{3}=\frac{z+28}{\lambda} \end{array} \)
through a point
\(\begin{array}{l} \overrightarrow{a}_2=\left(-26,-18,-28\right)\end{array} \)
parallel to
\(\begin{array}{l} \overrightarrow{b}_2=\left(-2,3,1\right) \end{array} \)
If lines are coplanar then,
\(\begin{array}{l} \left(\overrightarrow{a}_2-\overrightarrow{a}_1\right)\cdot\overrightarrow{b}_1\times\overrightarrow{b}_2=0\end{array} \)
\(\begin{array}{l} \Rightarrow\ \begin{vmatrix}27 & 20 & 31 \\\lambda & 1 & 2 \\-2 & 3 & \lambda \\\end{vmatrix}=0\Rightarrow \lambda =3\end{array} \)
Vector normal to the required plane
\(\begin{array}{l} \overrightarrow{n}=\overrightarrow{b}_1\times \overrightarrow{b}_2\end{array} \)
\(\begin{array}{l} \Rightarrow\ \overrightarrow{n}=\begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\3 & 1 & 2 \\-2 & 3 & 3 \\\end{vmatrix}=-3\hat{i}-13\hat{j}+11\hat{k}\end{array} \)
Equation of plane
\(\begin{array}{l} \equiv\left(\left(x-1\right),\left(y-2\right),\left(z-3\right)\right)\cdot\left(-3,-13,11\right)=0\end{array} \)
\(\begin{array}{l} \Rightarrow 3x+13y-11z+4=0 \end{array} \)
Checking the option gives (0, 4, 5) does not lie on the plane.
16. A plane P is parallel to two lines whose direction rations are –2, 1, –3 and –1, 2, –2 and it contains the point (2, 2, –2). Let P intersect the co-ordinate axes at the points A, B, C making the intercepts α, β, γ. If V is the volume of the tetrahedron OABC, where O is the origin and p = α + β + γ, then the ordered pair (V, p) is equal to :
(A) (48, –13)
(B) (24, –13)
(C) (48, 11)
(D) (24, –5)
Answer (B)
Sol. Let
\(\begin{array}{l} \overrightarrow{a}_1=\left(-2,1,-3\right) \end{array} \)
and \(\begin{array}{l} \overrightarrow{a}_2=\left(-1,2,-2\right)\end{array} \)
Vector normal to plane
\(\begin{array}{l} \overline{n}=\overrightarrow{a}_1\times \overrightarrow{a}_2\end{array} \)
\(\begin{array}{l} \overline{n}=\left(4,-1,-3\right) \end{array} \)
\(\begin{array}{l}\text{Plane through}\ (2, 2, -2)\ \text{and normal to}\ \overline{n}\end{array} \)
\(\begin{array}{l}\left(x – 2, y – 2, z + 2\right) \cdot \left(4, -1, -3\right) = 0\\ \Rightarrow 4x – y – 3z = 12\end{array} \)
\(\begin{array}{l} \Rightarrow\ \frac{x}{3}+\frac{y}{-12}+\frac{z}{-4}=1\end{array} \)
Interceptsα, β, γ are 3, –12, –4
P = α + β + γ = – 13
\(\begin{array}{l} V=\frac{1}{6}\times 3\times 12\times 4=24 \end{array} \)
17. Let S be the set of all a∈ R for which the angle between the vectors \(\begin{array}{l} \overrightarrow{u}=a\left(\text{log}_e b\right)\hat{i}-6\hat{j}+3\hat{k}\end{array} \)
and \(\begin{array}{l} \overrightarrow{v}=\left(\text{log}_e b\right)\hat{i}+2\hat{j}+2a\left(\text{log}_e b\right)\hat{k},\left(b>1\right)\end{array} \)
is acute. Then S is equal to
\(\begin{array}{l} (\text{A})\ \left(-\infty, -\frac{4}{3}\right)\end{array} \)
\(\begin{array}{l}(\text{B})\Phi \end{array} \)
\(\begin{array}{l} (\text{C})\ \left(-\frac{4}{3},0\right)\end{array} \)
\(\begin{array}{l} (\text{D})\ \left(\frac{12}{7},\infty\right)\end{array} \)
Answer (B)
Sol.
\(\begin{array}{l} \overrightarrow{u}=a\left(\text{log}_e b\right)\hat{i}-6\hat{j}+3\hat{k}\end{array} \)
\(\begin{array}{l} \overrightarrow{v}=\left(\text{log}_e b\right)\hat{i}+2\hat{j}+2a\left(\text{log}_e b\right)\hat{k} \end{array} \)
For acute angle,
\(\begin{array}{l} \overrightarrow{u}\cdot\overrightarrow{v}>0 \end{array} \)
\(\begin{array}{l} \Rightarrow\ a\left(\text{log}_e b\right)^2-12+6a\left(\text{log}_e b\right)>0\end{array} \)
∵ b > 1
Let
\(\begin{array}{l} \text{log}_e\ b=t\Rightarrow t>0 \text{ as }b>1 \end{array} \)
\(\begin{array}{l} at^2+6at-12>0~~\forall t>0 \end{array} \)
\(\begin{array}{l}\Rightarrow a \in \phi\end{array} \)
18. A horizontal park is in the shape of a triangle OAB with AB = 16. A vertical lamp post OP is erected at the point O such that \(\begin{array}{l}\angle PAO = \angle PBO = 15^\circ ~\text{and}~ \angle PCO = 45^\circ,\end{array} \)
where C is the midpoint of AB. Then (OP)2 is equal to
\(\begin{array}{l} (\text{A})\ \frac{32}{\sqrt{3}}\left(\sqrt{3}-1\right) \end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{32}{\sqrt{3}}\left(2-\sqrt{3}\right) \end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{16}{\sqrt{3}}\left(\sqrt{3}-1\right) \end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{16}{\sqrt{3}}\left(2-\sqrt{3}\right) \end{array} \)
Answer (B)
Sol.
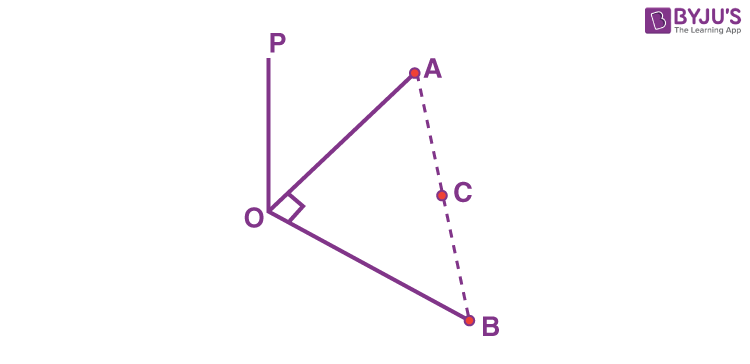
\(\begin{array}{l}OP = OA ~tan~15 = OB ~tan~ 15 \cdots \left(i\right)\\ OP = OC ~tan~ 45 \Rightarrow OP = OC \cdots \left(ii\right) \end{array} \)
\(\begin{array}{l}OA = OB \cdots \left(iii\right) \\ OC^2 + 8^2 = OA^2\end{array} \)
\(\begin{array}{l} OP^2+64=OP^2\left(\frac{\sqrt{3}+1}{\sqrt{3}-1}\right)^2\end{array} \)
\(\begin{array}{l} 64=OP^2\left[\frac{\left(\sqrt{3}+1\right)^2-\left(\sqrt{3}-1\right)^2}{\left(\sqrt{3}-1\right)^2}\right] \end{array} \)
\(\begin{array}{l} =OP^2\left(\frac{4\sqrt{3}}{\left(\sqrt{3}-1\right)^2}\right)\end{array} \)
\(\begin{array}{l} OP^2=\frac{64\left(\sqrt{3}-1\right)^2}{4\sqrt{3}}=\frac{32}{\sqrt{3}}\left(2-\sqrt{3}\right)\end{array} \)
19. Let A and B be two events such that \(\begin{array}{l} P\left(B/A\right)\frac{2}{5},\ P\left(A/B\right)=\frac{1}{7}\ \text{and}\ P\left(A\cap B\right)=\frac{1}{9}.\end{array} \)
Consider
\(\begin{array}{l} \left(S1\right)P\left(A’\cup B\right)=\frac{5}{6},\end{array} \)
\(\begin{array}{l} \left(S2\right)P\left(A’\cap B’\right)=\frac{1}{18}.\end{array} \)
Then
(A) Both (S1) and (S2) are true
(B) Both (S1) and (S2) are false
(C) Only (S1) is true
(D) Only (S2) is true
Answer (A)
Sol.
\(\begin{array}{l} P\left(A/B\right)=\frac{1}{7}\Rightarrow \frac{P\left(A\cap B\right)}{P\left(B\right)}=\frac{1}{7}\end{array} \)
\(\begin{array}{l} \Rightarrow P\left(B\right)=\frac{7}{9}\end{array} \)
\(\begin{array}{l} P\left(B/A\right)=\frac{2}{5}\Rightarrow \frac{P\left(A\cap B\right)}{P\left(A\right)}=\frac{2}{5} \end{array} \)
\(\begin{array}{l} P\left(A\right)=\frac{5}{2}\cdot \frac{1}{9}=\frac{5}{18}\end{array} \)
\(\begin{array}{l} S2:P\left(A’\cap B’\right)=\frac{1}{18}\end{array} \)
\(\begin{array}{l} S1:\text{ and }P\left(A’\cup B\right)=\frac{1}{9}+\frac{6}{9}+\frac{1}{18}=\frac{5}{6}.\end{array} \)
20. Let
p : Ramesh listens to music.
q :Ramesh is out of his village.
r : It is Sunday.
s : It is Saturday.
Then the statement “Ramesh listens to music only if he is in his village and it is Sunday or Saturday” can be expressed as
\(\begin{array}{l} \left(A\right) \left(\left(\sim q\right) \wedge \left(r\vee s\right)\right) \Rightarrow p\\ \left(B\right) \left(q\wedge \left(r\vee s \right)\right) \Rightarrow p\\ \left(C\right) p\Rightarrow \left(q\wedge \left(r\vee s\right)\right)\\ \left(D\right)p\Rightarrow \left(\sim q \right) \wedge \left(r\vee s\right)\end{array} \)
Answer (D)
Sol. p : Ramesh listens to music
q : Ramesh is out of his village
r : It is Sunday
s : It is Saturday
p→q conveys the same p only if q
Statement “Ramesh listens to music only if he is in his village and it is Sunday or Saturday”
p⇒ ((~ q) ∧ (r∨s))
SECTION – B
Numerical Value Type Questions: This section contains 10 questions. In Section B, attempt any five questions out of 10. The answer to each question is a NUMERICAL VALUE. For each question, enter the correct numerical value (in decimal notation, truncated/rounded-off to the second decimal place; e.g. 06.25, 07.00, –00.33, –00.30, 30.27, –27.30) using the mouse and the on-screen virtual numeric keypad in the place designated to enter the answer.
1. Let the coefficients of the middle terms in the expansion of \(\begin{array}{l} \left(\dfrac{1}{\sqrt 6}+ \beta x\right)^4, \left(1 – 3\beta x\right)^2 \text{and}\left(1 – \dfrac{\beta}{2}x\right )^6, \beta > 0,\end{array} \)
respectively form the first three terms of an A.P. If d is the common difference of this A.P., then \(\begin{array}{l} 50-\frac{2d}{\beta^2} \end{array} \)
is equal to _______.
Answer (57)
Sol. Coefficients of middle terms of given expansions are
\(\begin{array}{l} ^4C_2\frac{1}{6}\beta^2,\ ^2C_1\left(-3\beta\right),\ ^6C_3\left(\frac{-\beta}{2}\right)^3 \text{form an A.P.} \\\therefore\ 2.2\left(-3\beta\right)=\beta^2-\frac{5\beta^3}{2}\end{array} \)
\(\begin{array}{l}\Rightarrow -24 = 2\beta – 5\beta^2 \\ \Rightarrow 5\beta^2- 2\beta- 24 = 0\\ \Rightarrow 5\beta^2- 12\beta + 10\beta – 24 = 0\\ \Rightarrow \beta \left(5\beta- 12\right) + 2 \left(5\beta – 12\right) = 0\end{array} \)
\(\begin{array}{l}\beta = \frac{12}{5} \\ d = -6\beta – \beta^2\end{array} \)
\(\begin{array}{l} \therefore\ 50-\frac{2d}{\beta^2}=50-2\frac{\left(-6\beta-\beta^2\right)}{\beta^2}=50+\frac{12}{\beta}+2=57\end{array} \)
2. A class contains b boys and g girls. If the number of ways of selecting 3 boys and 2 girls from the class is 168, then b + 3 g is equal to ______.
Answer (17)
Sol.
\(\begin{array}{l}^bC_3\cdot ^gC_2 = 168\end{array} \)
\(\begin{array}{l} \Rightarrow \frac{b\left(b-1\right)\left(b-2\right)}{6}\cdot\frac{g\left(g-1\right)}{2}=168 \end{array} \)
\(\begin{array}{l}\Rightarrow b\left(b – 1\right) \left(b – 2\right) g\left(g – 1\right) = 2^5\cdot 3^2\cdot 7\\ \Rightarrow b\left(b – 1\right) \left(b – 2\right) g\left(g – 1\right) = 6. 7. 8. 3. 2\end{array} \)
∴ b = 8 and g = 3
∴ b + 3g = 17
3. Let the tangents at the points P and Q on the ellipse \(\begin{array}{l} \frac{x^2}{2}+\frac{y^2}{4}=1\ \text{meet at the point}\ R\left(\sqrt{2},2\sqrt{2}-2\right).\end{array} \)
If S is the focus of the ellipse on its negative major axis, then SP2 + SQ2 is equal to ________.
Answer (13)
Sol.
\(\begin{array}{l} E\equiv\frac{x^2}{2}+\frac{y^2}{4}=1 \end{array} \)
\(\begin{array}{l} T\equiv y=mx\pm \sqrt{2m^2+4}\\~~~~~~~~~~~~~~~~~~\downarrow \left(\sqrt{2},2\sqrt{2}-2\right) \end{array} \)
\(\begin{array}{l} \Rightarrow\ \left(2\sqrt{2}-2-m\sqrt{2}\right)=\pm\sqrt{2m^2+4} \end{array} \)
\(\begin{array}{l} \Rightarrow 2m^2-2m\sqrt{2}\left(2\sqrt{2}-2\right)+4\left(3-2\sqrt{2}\right)=2m^2+4\end{array} \)
\(\begin{array}{l} \Rightarrow\ -2\sqrt{2}m\left(2\sqrt{2}-2\right)=4-12+8\sqrt{2}\end{array} \)
\(\begin{array}{l} \Rightarrow\ -4\sqrt{2}m\left(\sqrt{2}-1\right)=8\left(\sqrt{2}-1\right)\end{array} \)
\(\begin{array}{l} \Rightarrow\ m=-\sqrt{2}\text{ and }m\rightarrow\infty\end{array} \)
\(\begin{array}{l}\therefore\text{Tangents are}~ x=\sqrt{2}\text{ and }y=-\sqrt{2}x+\sqrt{8} \end{array} \)
\(\begin{array}{l} \therefore\ P\left(\sqrt{2},0\right)\text{ and }Q\left(1,\sqrt{2}\right)\end{array} \)
and
\(\begin{array}{l} S=\left(0,-\sqrt{2}\right)\end{array} \)
\(\begin{array}{l}\therefore \left(PS\right)^2 + \left(QS\right)^2 = 4 + 9 = 13\end{array} \)
4. If \(\begin{array}{l}1 + \left(2 + ^{49}C_1 + ^{49}C_2 + … ^{49}C_{49}\right) \left(^{50}C_2 + ^{50}C_4 + … ^{50}C_{50}\right) \end{array} \)
is equal to 2n. m, where m is odd, then n + m is equal to ______.
Answer (99)
Sol.
\(\begin{array}{l}I = 1 + \left(1 + ^{49}C_0 + ^{49}C_1 + ….+ ^{49}C_{49}\right) \left(^{50}C_2 + ^{50}C_4 + … + ^{50}C_{50}\right)\\ \text{As} ^{49}C_0 + ^{49}C_1 + ….+ ^{49}C_{49} = 2^{49}\\ \text{and} ^{50}C_0 + ^{50}C_2 +…. + ^{50}C_{50} = 2^{49}\end{array} \)
⇒ 50C2 + 50C4 + … + 50C50 = 249 – 1
∴ I = 1 + (249 + 1)(249 – 1) = 298
∴ m = 1 and n = 98
m + n = 99
5. Two tangent lines l1 and l2 are drawn from the point (2, 0) to the parabola 2y2 = – x. If the lines l1 and l2 are also tangent to the circle (x – 5)2 + y2 = r, then 17r is equal to _________.
Answer (9)
Sol. Given:
\(\begin{array}{l} y^2=\frac{-x}{2}\end{array} \)
\(\begin{array}{l} T\equiv y=mx-\frac{1}{8m} \end{array} \)
\(\begin{array}{l} \downarrow \left(2,0\right) \end{array} \)
\(\begin{array}{l} \Rightarrow\ m^2=\frac{1}{16}\Rightarrow m=\pm \frac{1}{4}\end{array} \)
Tangents are
\(\begin{array}{l} y=\frac{1}{4}x-\frac{1}{2},y=\frac{-x}{4}+\frac{1}{2}\end{array} \)
4y = x – 2 and 4y + x = 2
If these are also tangent to circle then
dc = r
\(\begin{array}{l} \Rightarrow\ \left|\frac{5-2}{\sqrt{17}}\right|=\sqrt{r}\Rightarrow r=\left(\frac{3}{\sqrt{17}}\right)^2 \end{array} \)
\(\begin{array}{l} \Rightarrow\ 17r=17\cdot \frac{9}{17}=9\end{array} \)
6. If \(\begin{array}{l} \frac{6}{3^{12}}+\frac{10}{3^{11}}+\frac{20}{3^{10}}+\frac{40}{3^9}+\cdots +\frac{10240}{3}=2^n\cdot m, \end{array} \)
where m is odd, then m⋅n is equal to ________.
Answer (12)
Sol.
\(\begin{array}{l} \frac{1}{3^{12}}+5\left(\frac{2^0}{3^{12}}+\frac{2^1}{3^{11}}+\frac{2^2}{3^{10}}+\cdots +\frac{2^{11}}{3}\right)=2^n\cdot m\end{array} \)
\(\begin{array}{l} \Rightarrow\ \frac{1}{3^{12}}+5\left(\frac{1}{3^{12}}\frac{\left(\left(6\right)^2-1\right)}{\left(6-1\right)}\right)=2^n\cdot m\end{array} \)
\(\begin{array}{l} \Rightarrow\ \frac{1}{3^{12}}+\frac{5}{5}\left(\frac{1}{3^{12}}\cdot2^{12}\cdot 3^{12}-\frac{1}{3^{12}}\right)=2^n\cdot m\end{array} \)
\(\begin{array}{l} \Rightarrow\ \frac{1}{3^{12}}+2^{12}-\frac{1}{3^{12}}=2^n\cdot m\end{array} \)
⇒ 2n⋅m = 212
⇒ m = 1 and n = 12
m ⋅ n = 12
7. Let \(\begin{array}{l} S=\left[-\pi, \frac{\pi}{2}\right)-\left[-\frac{\pi}{2},-\frac{\pi}{4},-\frac{3\pi}{4},\frac{\pi}{4}\right].\end{array} \)
Then the number of elements in the set \(\begin{array}{l} A=\left\{\theta\in S:\tan\theta\left(1+\sqrt{5}\tan\left(2\theta\right)\right)=\sqrt{5}-\tan\left(2\theta\right) \right\} \end{array} \)
is ________.
Answer (5)
Sol. Let
\(\begin{array}{l} tan~\alpha =\sqrt{5}\end{array} \)
\(\begin{array}{l} \therefore\ \tan\theta=\frac{\tan\alpha-\tan2\theta}{1+\tan\alpha\tan2\theta} \end{array} \)
∴ tan θ = tan (α – 2θ)
α – 2θ = nπ + θ
⇒ 3θ = α – nπ
\(\begin{array}{l} \Rightarrow\ \theta = \frac{\alpha}{3}-\frac{n\pi}{3}~;~n\in Z\end{array} \)
If θ [–π, π/2) then
n = 0, 1, 2, 3, 4 are acceptable
∴ 5 solutions.
8. Let z = a + ib, b≠ 0 be complex numbers satisfying \(\begin{array}{l} z^2=\overline{z}\cdot 2^{1-\left|z\right|}.\end{array} \)
Then the least value of n∈ N, such that zn= (z + 1)n, is equal to _____.
Answer (6)
Sol.
\(\begin{array}{l} \because\ z^2=\overline{z}\cdot 2^{1-\left|z\right|}\cdots\left(1\right) \end{array} \)
\(\begin{array}{l} \Rightarrow\ \left|z\right|^2=\left|\overline{z}\right|\cdot 2^{1-\left|z\right|}\end{array} \)
\(\begin{array}{l} \Rightarrow\ \left|z\right|=2^{1-\left|z\right|},\because\ b\neq0\Rightarrow \left|z\right|\neq 0 \end{array} \)
∴ |z| = 1 …(2)
\(\begin{array}{l}\because z = a + ib\ \text{then}\ \sqrt{a^2+b^2}=1 \cdots (3)\end{array} \)
Now again from equation (1), equation (2), equation (3) we get :
a2 – b2 + i2ab = (a – ib) 20
∴ a2 – b2 =a and 2ab = – b
\(\begin{array}{l}\therefore \ a=-\frac{1}{2}\text{ and }b=\pm \frac{\sqrt{3}}{2}\end{array} \)
\(\begin{array}{l} \therefore\ z=-\frac{1}{2}+\frac{\sqrt{3}}{2}i\text{ or }z=-\frac{1}{2}-\frac{\sqrt{3}}{2}i\end{array} \)
\(\begin{array}{l} z^n=\left(z+1\right)^n\Rightarrow \left(\frac{z+1}{z}\right)^n=1\end{array} \)
\(\begin{array}{l} \left(1+\frac{1}{z}\right)^n=1\end{array} \)
\(\begin{array}{l} \left(\frac{1+\sqrt{3}i}{2}\right)^n=1\end{array} \)
, then minimum value of n is 6.
9. A bag contains 4 white and 6 black balls. Three balls are drawn at random from the bag. Let X be the number of white balls, among the drawn balls. If σ2 is the variance of X, then 100 σ2 is equal to ____.
Answer (56)
Sol. X = Number of white ball drawn
\(\begin{array}{l} P\left(X=0\right)=\frac{^6C_3}{^{10}C_3}=\frac{1}{6}\end{array} \)
\(\begin{array}{l} P\left(X=1\right)=\frac{^6C_2\times~^4C_1}{^{10}C_3}=\frac{1}{2} \end{array} \)
\(\begin{array}{l} P\left(X=2\right)=\frac{^6C_1\times~^4C_2}{^{10}C_3}=\frac{3}{10} \end{array} \)
and
\(\begin{array}{l} P\left(X=3\right)=\frac{^6C_0\times~^4C_3}{^{10}C_3}=\frac{1}{30}\end{array} \)
\(\begin{array}{l} \text{Variance} = \sigma^2=\Sigma P_iX_i^2-\left(\Sigma P_iX_i\right)^2\end{array} \)
\(\begin{array}{l} \sigma^2=\frac{1}{2}+\frac{12}{10}+\frac{3}{10}-\left(\frac{1}{2}+\frac{6}{10}+\frac{1}{10}\right)^2\end{array} \)
\(\begin{array}{l} =\frac{56}{100}\end{array} \)
100σ2 = 56.
10. The value of the integral \(\begin{array}{l} \displaystyle\int\limits_0^{\frac{\pi}{2}}60\frac{\sin\left(6x\right)}{\sin x}dx \end{array} \)
is equal to ______.
Answer (104)
Sol.
\(\begin{array}{l} I=\displaystyle\int\limits_0^{\frac{\pi}{2}}60\cdot\frac{\sin6x}{\sin x}dx \end{array} \)
\(\begin{array}{l} =60.2\displaystyle\int\limits_0^{\frac{\pi}{2}}\left(3-4\sin^2x\right)\left(4\cos^2x-3\right)\cos xdx\end{array} \)
\(\begin{array}{l} =120\displaystyle\int\limits_0^{\frac{\pi}{2}}\left(3-4\sin^2x\right)\left(1-4\sin^2x\right)\cos xdx\end{array} \)
Let sinx = t ⇒ cos x dx = dt
\(\begin{array}{l} =120\displaystyle\int\limits_0^1\left(3-4t^2\right)\left(1-4t^2\right)dt\end{array} \)
\(\begin{array}{l} =120\displaystyle\int\limits_0^1\left(3-16t^2+16t^4\right)dt\end{array} \)
\(\begin{array}{l} =120\left[3t-\frac{16t^3}{3}+\frac{16t^5}{5}\right]_0^1\\= 104 \end{array} \)
JEE Main 2022 July 28th Shift 2 Paper Analysis













Comments