The JEE Main 2022 June 25 – Shift 2 Maths Question Paper with Solutions are provided on this page. JEE Main 2022 answer keys are prepared by subject matter experts at BYJU’S. These are prepared in a step-by-step manner, to help students easily understand the tricks used in solving the problems. Students can also download the JEE Main 2022 June 25 – Shift 2 Maths Question Paper with Solutions in PDF format. Practising the JEE Main 2022 question papers will help students to prepare effectively for the upcoming exams. It will also help them to evaluate the difficulty level of the JEE Main 2022 exam.
JEE Main 2022 June 25th Shift 2 Maths Question Paper and Solutions
SECTION – A
Multiple Choice Questions: This section contains 20 multiple choice questions. Each question has 4 choices (1), (2), (3) and (4), out of which ONLY ONE is correct.
Choose the correct answer :
1. Let A = {x ∈ R : | x + 1 | < 2} and B = {x ∈ R : | x – 1| ≥ 2}. Then which one of the following statements is NOT true?
(A) A – B = (–1, 1)
(B) B – A = R – (–3, 1)
(C) A ⋂ B = (–3, –1]
(D) A U B = R – [1, 3)
Answer (B)
Sol. A = (–3, 1) and B = (–∞, –1] ∪ [3, ∞)
So, A – B = (–1, 1)
B – A = (–∞, –3] ∪ [3, ∞) = R – (–3, 3)
A ∩ B = (–3, –1]
and A ∪ B = (–∞, 1) ∪ [3, ∞) = R – [1, 3)
2. Let a, b ∈ R be such that the equation ax2 – 2bx + 15 = 0 has a repeated root α. If α and β are the roots of the equation x2 – 2bx + 21 = 0, then α2 + β2 is equal to
(A) 37
(B) 58
(C) 68
(D) 92
Answer (B)
Sol. ax2 – 2bx + 15 = 0 has repeated root so b2 = 15a
and
\(\begin{array}{l}\alpha =\frac{15}{b}\end{array} \)
∵α is a root of x2 – 2bx + 21 = 0
So
\(\begin{array}{l}\frac{225}{b^2}=9\Rightarrow b^2=25\end{array} \)
Now α2 + β2 = (α + β)2 – 2αβ = 4b2 – 42 = 100 – 42
= 58
3. Let z1 and z2 be two complex numbers such that \(\begin{array}{l}\overline{z_1}=i\overline{z_2}\ \text{and}\ arg\left( \frac{z_1}{\overline{z_2}} \right )=\pi.\end{array} \)
Then
\(\begin{array}{l}(A)\ arg~ z_2=\left (\frac{\pi}{4}\right )\end{array} \)
\(\begin{array}{l}(B)\ arg z_2=-\frac{3\pi}{4}\end{array} \)
\(\begin{array}{l}(C)\ arg~ z_1=\frac{\pi}{4}\end{array} \)
\(\begin{array}{l}(D)\ arg z_1=-\frac{3\pi}{4}\end{array} \)
Answer (C)
Sol.
\(\begin{array}{l}\because \frac{z_1}{z_2}=-i\Rightarrow z_1=-iz_2 \end{array} \)
\(\begin{array}{l}\Rightarrow arg(z_1)=-\frac{\pi}{2}+arg(z_2)……(i)\end{array} \)
Also
\(\begin{array}{l}arg(z_1)-arg(\overline{z}_2)=\pi\end{array} \)
⇒ arg(z1) + arg(z2) = π …(ii)
From (i) and (ii), we get
\(\begin{array}{l}arg(z_1)=\frac{\pi}{4} and~arg(z_2)=\frac{3\pi}{4}\end{array} \)
4. The system of equations
–kx + 3y – 14z = 25
–15x + 4y – kz = 3
–4x + y + 3z = 4
is consistent for all k in the set
(A) R
(B) R – {–11, 13}
(C) R – {13}
(D) R – {–11, 11}
Answer (D)
Sol. The system may be inconsistent if
\(\begin{array}{l}\begin{vmatrix}-k &3 &-14 \\-15 &4 &-k \\-4 &1 &3 \\\end{vmatrix}=0\Rightarrow k=\pm 11\end{array} \)
Hence if system is consistent then
\(\begin{array}{l}k\in R-\left\{11,-11\right\}\end{array} \)
5. \(\begin{array}{l}\displaystyle \lim_{x\to \frac{\pi}{2}}tan^2x\left((2sin^2x+3sinx+4)^{\frac{1}{2}}-(sin^2x+6sinx+2)^{\frac{1}{2}}\right)\end{array} \)
is equal to
(A) 1/12
(B) -1/18
(C) -1/12
(D) 1/6
Answer (A)
Sol.
\(\begin{array}{l}\displaystyle \lim_{x\to \frac{\pi}{2}}tan^2x\left\{\sqrt{2sin^2x+3sinx+4}-\sqrt{sin^2x+6sinx+2}\right\}\end{array} \)
\(\begin{array}{l}=\displaystyle \lim_{x\to \frac{\pi}{2}}\frac{tan^2x(sin^2x-3sinx+2)}{\sqrt{2sin^2x+3sinx+4}+\sqrt{sin^2x+6sinx+2}}\end{array} \)
\(\begin{array}{l}=\frac{1}{6}\displaystyle \lim_{x\to \frac{\pi}{2}}\frac{(1-sinx)(2-sinx)}{cos^2x}.sin^2x\end{array} \)
\(\begin{array}{l}=\frac{1}{6}\displaystyle \lim_{x\to \frac{\pi}{2}}\frac{(2-sinx)sin^2x }{1+sinx}\end{array} \)
\(\begin{array}{l}=\frac{1}{12}\end{array} \)
6. The area of the region enclosed between the parabolas y2 = 2x – 1 and y2 = 4x – 3 is
(A) ⅓
(B) ⅙
(C) ⅔
(D) ¾
Answer (A)
Sol. Area of the shaded region
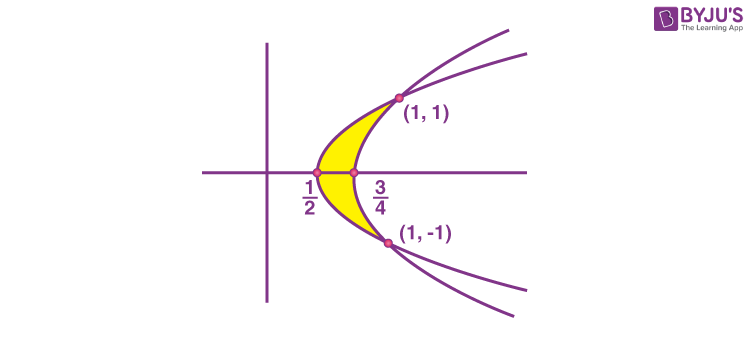
\(\begin{array}{l}=2\int_{0}^{1}\left(\frac{y^2+3}{4}-\frac{y^2+1}{2}\right )dy\end{array} \)
\(\begin{array}{l}=2\int_{0}^{1}\left(\frac{1}{4}-\frac{y^2}{4}\right )dy\end{array} \)
\(\begin{array}{l}=2\left[\frac{1}{4}-\frac{1}{12}\right]=\frac{1}{3}\end{array} \)
7. The coefficient of x101 in the expression (5 + x)500 + x(5 + x)499 + x2(5 + x)498 + ……+ x500, x > 0, is
(A) 501C101 (5)399
(B) 501C101 (5)400
(C) 501C100 (5)400
(D) 500C101 (5)399
Answer (A)
Sol.
\(\begin{array}{l}\text{Coeff. of}\ x^{101}in\ \frac{x^{500}\left [ \left ( \frac{x+5}{x}\right)^{501}-1 \right ]}{\frac{x+5}{x}-1}\end{array} \)
\(\begin{array}{l}=\text{Coeff. of}\ x^{101}in\ \frac{1}{5}\left[(x+5)^{501}-x^{501}\right ]\end{array} \)
\(\begin{array}{l}=\frac{1}{5}^{501}C_{101}.5^{400}\end{array} \)
\(\begin{array}{l}=_{}^{501}C_{101}\textrm{}.5^{399}\end{array} \)
8. The sum 1 + 2 ⋅ 3 + 3 ⋅ 32 + …. + 10 ⋅ 39 is equal to
\(\begin{array}{l}(A)\ \frac{2.3^{12}+10}{4}\end{array} \)
\(\begin{array}{l}(B)\ \frac{19.3^{10}+1}{4}\end{array} \)
\(\begin{array}{l}(C)\ 5.3^{10}-2\end{array} \)
\(\begin{array}{l}(D)\ \frac{9.3^{10}+1}{2}\end{array} \)
Answer (B)
Sol. Let
\(\begin{array}{l}\begin{matrix}S=1.3^{\circ}+2.3^1+3.3^2+……..+10.3^9\\\underline{3S= 1.3^1+2.3^2+…………….+10.3^{10}}\\-2S=(1.3^{\circ}+1.3^1+1.3^2+….+1.3^9)-10.3^{10}\end{matrix}\end{array} \)
\(\begin{array}{l}\Rightarrow S=\frac{1}{2}\left [ 10.3^{10}-\frac{3^{10}-1}{3-1}\right ]\end{array} \)
\(\begin{array}{l}\Rightarrow S=\frac{19.3^{10}+1}{4}\end{array} \)
9. Let P be the plane passing through the intersection of the planes \(\begin{array}{l}\overrightarrow{r}.(\hat{i}+3\hat{j}-\hat{k})=5 ~and~ \overrightarrow{r}~.(2\hat{i}-\hat{j}+\hat{k})=3,\end{array} \)
and the point (2, 1, –2). Let the position vectors of the points X and Y be \(\begin{array}{l}\hat{i}-2\hat{j}+4\hat{k}\ \text{and}\ 5\hat{i}-\hat{j}+2\hat{k}\end{array} \)
respectively. Then the points
(A) X and X + Y are on the same side of P
(B) Y and Y – X are on the opposite sides of P
(C) X and Y are on the opposite sides of P
(D) X + Y and X – Y are on the same side of P
Answer (C)
Sol. Let the equation of required plane
\(\begin{array}{l}\pi:(x+3y-z-5)+\lambda (2x-y+z-3)=0\end{array} \)
\(\begin{array}{l}\because (2,1,-2) \text{lies on it so,}\ 2+\lambda (-2)=0\end{array} \)
⇒ λ = 1
Hence,
\(\begin{array}{l}\pi:3x+2y-8=0\end{array} \)
\(\begin{array}{l}\because \pi_x=-9, \pi_y=5, \pi_{x+y}=4 \end{array} \)
\(\begin{array}{l}\pi_{x-y}=-22 and \pi_{y-x}=6 \end{array} \)
Clearly, X and Y are on opposite sides of plane π.
10. A circle touches both the y-axis and the line x + y = 0. Then the locus of its center is
\(\begin{array}{l}(A)\ y=\sqrt{2}x\end{array} \)
\(\begin{array}{l}(B)\ x=\sqrt{2}y\end{array} \)
\(\begin{array}{l}(C)\ y^2-x^2=2xy\end{array} \)
\(\begin{array}{l}(D)\ x^2-y^2=2xy\end{array} \)
Answer (D)
Sol. Let the centre be (h, k)
So,
\(\begin{array}{l}\left|h\right|=\left|\frac{h+k}{\sqrt{2}}\right|\end{array} \)
⇒ 2h2 = h2 + k2 + 2hk
Locus will be x2 – y2 = 2xy
11. Water is being filled at the rate of 1 cm3/sec in a right circular conical vessel (vertex downwards) of height 35 cm and diameter 14 cm. When the height of the water level is 10 cm, the rate (in cm2/sec) at which the wet conical surface area of the vessel increase, is
(A) 5
\(\begin{array}{l}(B)\ \frac{\sqrt{21}}{5}\end{array} \)
\(\begin{array}{l}(C)\ \frac{\sqrt{26}}{5}\end{array} \)
\(\begin{array}{l}(D)\ \frac{\sqrt{26}}{10}\end{array} \)
Answer (C)
Sol.
\(\begin{array}{l}\because V=\frac{1}{3}\pi r^2h \text{and}\ \frac{r}{h}=\frac{7}{35}=\frac{1}{5} \end{array} \)
\(\begin{array}{l}\Rightarrow V=\frac{1}{75}\pi h^3\end{array} \)
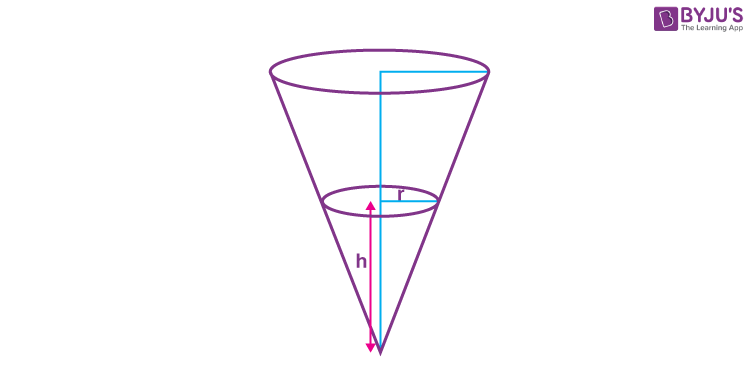
\(\begin{array}{l}\frac{dV}{dt}=\frac{1}{25}\pi h^2\frac{dh}{dt}=1\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{dh}{dt}=\frac{25}{\pi h^2}\end{array} \)
Now,
\(\begin{array}{l}S=\pi rl=\pi\left ( \frac{h}{5}\right)\sqrt{h^2+\frac{h^2}{25}}=\frac{\pi}{25}\sqrt{26}h^2\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{dS}{dt}=\frac{2\sqrt{26}\pi h}{25}.\frac{dh}{dt}=\frac{2\sqrt{26}}{h}\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{dS}{dt}_{(h=10)}=\frac{\sqrt{26}}{5}\end{array} \)
12. If \(\begin{array}{l}b_n=\int_{0}^{\frac{\pi}{2}}\frac{cos^2nx}{sinx}dx,n\epsilon N,\end{array} \)
then
(A) b3 – b2, b4 – b3, b5 – b4 are in an A.P. with a common difference –2
\(\begin{array}{l}(B)\ \frac{1}{b_3-b_2},\frac{1}{b_4-b_3},\frac{1}{b_5-b_4}\ \text{are in an A. P. with common difference 2}\end{array} \)
(C) b3 – b2, b4 – b3, b5 – b4 are in a G.P.
\(\begin{array}{l}(D)\ \frac{1}{b_3-b_2},\frac{1}{b_4-b_3},\frac{1}{b_5-b_4}\ \text{are in an A.P. with common difference –2}\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l}b_n-b_{n-1}=\int_{0}^{\frac{\pi}{2}}\frac{cos^2nx-cos^2(n-1)}{sinx}dx\end{array} \)
\(\begin{array}{l}=\int_{0}^{\pi/2}\frac{-sin(2n-1)x.sinx}{sinx}dx\end{array} \)
\(\begin{array}{l}\left.\begin{matrix}=\frac{cos(2n-1)x}{2n-1} \\\end{matrix}\right|_{0}^{\pi/2}=-\frac{1}{2n-1}\end{array} \)
So, b3 – b2, b4 – b3, b5 – b4 are in H.P.
\(\begin{array}{l}\Rightarrow \frac{1}{b_3-b_2},\frac{1}{b_4-b_3},\frac{1}{b_5-b_4}\end{array} \)
are in A. P. with common difference –2.
13. If y = y(x) is the solution of the differential equation \(\begin{array}{l}2x^2\frac{dy}{dx}-2xy+3y^2=0\ \text{such that}\ y(e)=\frac{e}{3},\end{array} \)
then y(1) is equal to
(A) ⅓
(B) ⅔
(C) 3/2
(D) 3
Answer (B)
Sol.
\(\begin{array}{l}2x^2\frac{dy}{dx}-2xy+3y^2=0\end{array} \)
\(\begin{array}{l}\Rightarrow 2x(xdy-ydx)+3y^2dx=0\end{array} \)
\(\begin{array}{l}\Rightarrow 2\left (\frac{xdy-ydx}{y^2}\right)+3\frac{dx}{x}=0\end{array} \)
\(\begin{array}{l}\Rightarrow -\frac{2x}{y}+3Inx=C\end{array} \)
\(\begin{array}{l}\because y(e)=\frac{e}{3}\Rightarrow -6+3=C \Rightarrow C=-3\end{array} \)
Now,at
\(\begin{array}{l}x=1,-\frac{2}{y}+0=-3\end{array} \)
\(\begin{array}{l}y=\frac{2}{3}\end{array} \)
14. If the angle made by the tangent at the point (x0, y0) on the curve x = 12(t + sin t cos t), \(\begin{array}{l}y=12(1+\sin t)^2,0<t<\frac{\pi}{2},\end{array} \)
with the positive x-axis is π/3, then y0 is equal to:
\(\begin{array}{l}(A)\ 6(3+2\sqrt{2})\end{array} \)
\(\begin{array}{l}(B)\ 3(7+4\sqrt{3})\end{array} \)
(C) 27
(D) 48
Answer (C)
Sol.
\(\begin{array}{l}\because \frac{dy}{dx}=\frac{24(1+sint)cost}{12(1+cos2t)}=\frac{1+sint}{cost}=tan\left(\frac{\pi}{4}+\frac{t}{2}\right ) \end{array} \)
\(\begin{array}{l}\because \frac{dy}{dx}_{(x_0,y_0)}=\sqrt{3}=tan\left(\frac{\pi}{4}+\frac{t}{2}\right) \end{array} \)
\(\begin{array}{l}\Rightarrow t=\frac{\pi}{6}\end{array} \)
So,
\(\begin{array}{l}y_{0\left(at~ t=\frac{\pi}{6}\right )}=12\left (1+sin\frac{\pi}{6}\right)^2=27\end{array} \)
15. The value of 2 sin(12°) – sin(72°) is :
\(\begin{array}{l}(A)\ \frac{\sqrt{5}(1-\sqrt{3})}{4}\end{array} \)
\(\begin{array}{l}(B)\ \frac{1-\sqrt{5})}{8}\end{array} \)
\(\begin{array}{l}(C)\ \frac{\sqrt{3}(1-\sqrt{5})}{2}\end{array} \)
\(\begin{array}{l}(D)\ \frac{\sqrt{3}(1-\sqrt{5})}{4}\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l}2sin12^{\circ}-sin72^{\circ}\end{array} \)
\(\begin{array}{l}=sin12^{\circ}+(-2cos42^{\circ}.sin30^{\circ})\end{array} \)
\(\begin{array}{l}=sin12^{\circ}-cos42^{\circ}\end{array} \)
\(\begin{array}{l}=sin12^{\circ}-sin48^{\circ}\end{array} \)
\(\begin{array}{l}=2sin18^{\circ}.cos30^{\circ}\end{array} \)
\(\begin{array}{l}=-2\left(\frac{\sqrt{5}-1}{4}\right).\frac{\sqrt{3}}{2}\end{array} \)
\(\begin{array}{l}=\frac{\sqrt{3}(1-\sqrt{5})}{4}\end{array} \)
16. A biased die is marked with numbers 2, 4, 8, 16, 32, 32 on its faces and the probability of getting a face with mark n is 1/n. If the die is thrown thrice, then the probability, that the sum of the numbers obtained is 48, is :
\(\begin{array}{l}(A)\ \frac{7}{2^{11}}\end{array} \)
\(\begin{array}{l}(B)\ \frac{7}{2^{12}}\end{array} \)
\(\begin{array}{l}(C)\ \frac{3}{2^{10}}\end{array} \)
\(\begin{array}{l}(D)\ \frac{13}{2^{12}}\end{array} \)
Answer (D)
Sol. There are only two ways to get sum 48, which are (32, 8, 8) and (16, 16, 16)
So, the required probability
\(\begin{array}{l}=3\left(\frac{2}{32}.\frac{1}{8}.\frac{1}{8}\right)+\left(\frac{1}{16}.\frac{1}{16}.\frac{1}{16}\right)\end{array} \)
\(\begin{array}{l}=\frac{3}{2^{10}}+\frac{1}{2^{12}}\end{array} \)
\(\begin{array}{l}=\frac{13}{2^{12}}\end{array} \)
17. The negation of the Boolean expression ((~ q) ∧ p) ⇒ ((~ p) ∨ q) is logically equivalent to :
(A) p ⇒ q
(B) q ⇒ p
(C) ~ (p ⇒ q)
(D) ~ (q ⇒ p)
Answer (C)
Sol. Let S : ((~ q) ∧ p) ⇒ ((~ p) ∨ q)
⇒ S : ~ ((~ q) ∧ p) ∨ ((~ p) ∨ q)
⇒ S : (q ∨ (~ p)) ∨ ((~ p) ∨ q)
⇒ S : (~ p) ∨ q
⇒ S : p ⇒ q
So, negation of S will be ~ (p ⇒ q)
18. If the line y = 4 + kx, k > 0, is the tangent to the parabola y = x – x2 at the point P and V is the vertex of the parabola, then the slope of the line through P and V is :
\(\begin{array}{l}(A)\ \frac{3}{2}\end{array} \)
\(\begin{array}{l}(B)\ \frac{26}{9}\end{array} \)
\(\begin{array}{l}(C)\ \frac{5}{2}\end{array} \)
\(\begin{array}{l}(D)\ \frac{23}{6}\end{array} \)
Answer (C)
Sol. ∵ Line y = kx + 4 touches the parabola y = x – x2.
So, kx + 4 = x – x2 ⇒ x2 + (k – 1) x + 4 = 0 has only one root
(k – 1)2 = 16 ⇒ k = 5 or – 3 but k > 0
So, k = 5.
And hence x2 + 4x + 4 = 0 ⇒ x = – 2
So, P(–2, –6) and V is
\(\begin{array}{l}\left(\frac{1}{2},\frac{1}{4}\right)\end{array} \)
Slope of PV
\(\begin{array}{l}=\frac{\frac{1}{4}+6}{\frac{1}{2}+2}=\frac{5}{2}\end{array} \)
19. The value of \(\begin{array}{l}tan^{-1}\left(\frac{cos\frac{15\pi}{4}-1}{sin\left(\frac{\pi}{4}\right)}\right )\end{array} \)
is equal to :
\(\begin{array}{l}(A)\ -\frac{\pi}{4}\end{array} \)
\(\begin{array}{l}(B)\ -\frac{\pi}{8}\end{array} \)
\(\begin{array}{l}(C)\ -\frac{5\pi}{12}\end{array} \)
\(\begin{array}{l}(D)\ -\frac{4\pi}{9}\end{array} \)
Answer (B)
Sol.
\(\begin{array}{l}tan^{-1}\left ( \frac{cos\left ( \frac{15\pi}{4} \right )-1}{sin\frac{\pi}{4}}\right )\end{array} \)
\(\begin{array}{l}=tan^{-1}\left(\frac{\frac{1}{\sqrt{2}}-1}{\frac{1}{\sqrt{2}}} \right )\end{array} \)
\(\begin{array}{l}=tan^{-1}(1-\sqrt{2})=-tan^{-1}(\sqrt{2}-1)\end{array} \)
\(\begin{array}{l}=-\frac{\pi}{8}\end{array} \)
20. The line y = x + 1 meets the ellipse \(\begin{array}{l}\frac{x^2}{4}+\frac{y^2}{2}=1\end{array} \)
at two points P and Q. If r is the radius of the circle with PQ as diameter then (3r)2 is equal to :
(A) 20
(B) 12
(C) 11
(D) 8
Answer (A)
Sol. Let point (a, a + 1) as the point of intersection of line and ellipse.
So,
\(\begin{array}{l}\frac{a^2}{4}+\frac{(a+1)^2}{2}=1\Rightarrow a^2+2(a^2+2a+1)=4\end{array} \)
\(\begin{array}{l}\Rightarrow 3a^2+4a-2=0\end{array} \)
If the roots of this equation are α and β.
So, P(α, α + 1) and Q(β, β + 1)
PQ2 = 4r2 = (α – β)2 + (α – β)2
\(\begin{array}{l}\Rightarrow 9r^2=\frac{9}{4}(2(\alpha -\beta )^2)\end{array} \)
\(\begin{array}{l}=\frac{9}{2}\left[(\alpha +\beta)^2-4\alpha \beta\right ]\end{array} \)
\(\begin{array}{l}=\frac{9}{2}\left [\left ( -\frac{4}{3} \right)^2+\frac{8}{3} \right ]\end{array} \)
\(\begin{array}{l}=\frac{1}{2}[16+24]=20\end{array} \)
SECTION – B
Numerical Value Type Questions: This section contains 10 questions. In Section B, attempt any five questions out of 10. The answer to each question is a NUMERICAL VALUE. For each question, enter the correct numerical value (in decimal notation, truncated/rounded-off to the second decimal place; e.g. 06.25, 07.00, –00.33, –00.30, 30.27, –27.30) using the mouse and the on-screen virtual numeric keypad in the place designated to enter the answer.
1. \(\begin{array}{l}\text{Let}\ A=\begin{pmatrix}2 &-2\\1 &-1\\\end{pmatrix}\ \text{and}\ B=\begin{pmatrix}-1 &2\\-1 &2\\\end{pmatrix}.\end{array} \)
Then the number of elements in the set {(n, m) : n, m ∈ { 1, 2……….., 10} and nAn + mBm = I} is ____________.
Answer (1)
Sol.
\(\begin{array}{l}A^2=\begin{bmatrix}2 &-2 \\1 &-1 \\\end{bmatrix}\begin{bmatrix}2 &-2 \\1 & -1 \\\end{bmatrix}\end{array} \)
\(\begin{array}{l}=\begin{bmatrix}2 &-2 \\1 &-1 \\\end{bmatrix}=A \Rightarrow A^K=A, K\in l\end{array} \)
\(\begin{array}{l}B^2=\begin{bmatrix}-1 &2 \\-1 &2 \\\end{bmatrix}\begin{bmatrix}-1 &2 \\-1 &2 \\\end{bmatrix}=\begin{bmatrix}-1 &2 \\-1 &2 \\\end{bmatrix}=B\end{array} \)
So, BK = B, K ∈ I
nA^n + mB^m = nA + mB
\(\begin{array}{l}=\begin{bmatrix}2n-2n\\n-n \\\end{bmatrix}+\begin{bmatrix}-m &2m \\-m &2m \\\end{bmatrix}\end{array} \)
\(\begin{array}{l}\begin{bmatrix}1 &0 \\0 &1 \\\end{bmatrix}\end{array} \)
So, 2n – m = 1, –n + m = 0, 2m – n = 1
So, (m, n) = (1, 1)
2. Let f(x) = [2x2 + 1] and \(\begin{array}{l}g(x) = \left\{\begin{matrix}2x-3, &x<0\\2x+3, &x\geq 0\\\end{matrix}\right.\end{array} \)
, where [t] is the greatest integer ≤ t. Then, in the open interval (–1, 1), the number of points where fog is discontinuous is equal to _______.
Answer (62)
Sol.
\(\begin{array}{l}f(g(x))=\left\{\begin{matrix}[2(2x-3)^2]+1, x<0& \\ [2(2x+3)^2]+1, x\geq 0&\\\end{matrix}\right.\end{array} \)
The possible points where fog(x) may be discontinuous are
2(2x – 3)2 ∈ I & x ∈ (–1, 0)
2(2x + 3)2 ∈ I & x ∈ [0, 1)
| x ∈ (–1, 0)
2x – 3 ∈ (–5, –3)
2(2x – 3)2 ∈ (18, 50)
So, no. of points = 31 |
x ∈ [0, 1)
2x + 3 ∈ [3, 5)
2(2x + 3)2 ∈ [18, 50)
It is discontinuous at all points except x = 0 of no. points = 31 |
So, total = 62
3. The value of b > 3 for which \(\begin{array}{l}12\int _{3}^{b}\frac{1}{(x^2-1)(x^2-4)}dx=log_e\left ( \frac{49}{40} \right ),\end{array} \)
is equal to
Answer (6)
Sol.
\(\begin{array}{l}l=\int \frac{1}{(x^2-1)(x^2-4)}dx=\frac{1}{3}\int \left ( \frac{1}{x^2-4}-\frac{1}{x^2-1} \right)dx\end{array} \)
\(\begin{array}{l}=\frac{1}{3}\left(\frac{1}{4}In\left|\frac{x-2}{x+2}\right|-\frac{1}{2}In\left|\frac{x-1}{x+1}\right|\right)+C\end{array} \)
\(\begin{array}{l}12l=In\left|\frac{x-2}{x+2}\right|-2In\left|\frac{x-1}{x+1}\right|+C\end{array} \)
\(\begin{array}{l}12\int_{3}^{b}\frac{dx}{(x^2-4)(x^2-1)}=In\left(\frac{b-2}{b+2}\right)-2In\left(\frac{b-1}{b+1}\right)-\left(In\left(\frac{1}{5}\right )-2In\left (\frac{1}{2} \right ) \right )\end{array} \)
\(\begin{array}{l}=In\left(\left(\frac{b-2}{b+2}\right)\frac{(b+1)^2}{(b-1)^2}\right)-\left(In\frac{4}{5}\right)\end{array} \)
\(\begin{array}{l}So,\frac{49}{40}=\frac{(b-2)}{(b+2)}\frac{(b+1)^2}{(b-1)^2}.\frac{5}{4}\end{array} \)
⇒ b = 6
4. If the sum of the co-efficients of all the positive even powers of x in the binomial expansion of \(\begin{array}{l}\left(2x^3+\frac{3}{x}\right)^{10}\end{array} \)
is 510 – β·39, the β is equal to ____.
Answer (83)
Sol.
\(\begin{array}{l}T_{r+1}=^{10}C_{r}(2x^3)^{10-r}\left(\frac{3}{x}\right)^r\end{array} \)
\(\begin{array}{l}=^{10}C_{r}2^{10-r}3^rx^{30-4r}\end{array} \)
So, r ≠ 8, 9, 10
Sum of required Coeff.
\(\begin{array}{l}=\left ( 2.1^3+\frac{3}{1}\right)^{10}\left(^{10}C_{8}2^23^8+^{10}C_{9}2^13^9+^{10}C_{10}2^03^{10}\right)\end{array} \)
\(\begin{array}{l}=5^{10}-3^9\left(\frac{^{10}C_8.2^2}{3}+^{10}C_9.2^1+^{10}C_{10}.3\right )\end{array} \)
\(\begin{array}{l}\beta =\frac{4}{3}.^{10}C_8+20+3=83 \end{array} \)
5. If the mean deviation about the mean of the numbers 1, 2, 3, …. n, where n is odd, is 5(n + 1)/n, then n is equal to ___________.
Answer (21)
Sol. Mean
\(\begin{array}{l}=\frac{\frac {n(n+1)}{2}}{n}=\frac{n+1}{2}\end{array} \)
\(\begin{array}{l}M.D=\frac{2\left(\frac{n-1}{2}+\frac{n-3}{2}+\frac{n-5}{2}+…0\right )}{n}=\frac{5(n+1)}{n}\end{array} \)
\(\begin{array}{l}\Rightarrow ((n-1)+(n-3)+(n-5)+…0)=5(n+1)\end{array} \)
\(\begin{array}{l}\Rightarrow \left(\frac{n+1}{4}.\right)(n-1)=5(n+1)\end{array} \)
So, n = 21
6. \(\begin{array}{l}\text{Let}\ \vec{b}=\hat{i}+\hat{j}+\lambda \hat{k},\lambda \in\mathbb{R}.\ \text{If}\ \vec{a}\ \text{is a vector such that}\end{array} \)
\(\begin{array}{l}\vec{a}\times \vec{b}=13\hat{i}-\hat{j}-4\hat{k}\ \text{and}\ vec{a}.\vec{b}+21=0,\ \text{then}\end{array} \)
\(\begin{array}{l}(\vec{b}-\vec{a}).(\hat{k}-\hat{j})+(\vec{b}+\vec{a}).(\hat{i}-\hat{k})\end{array} \)
is equal to
Answer (14)
Sol. Let
\(\begin{array}{l}\vec{a}=x\hat{i}=y\hat{j}+z\hat{k}\end{array} \)
So,
\(\begin{array}{l}\begin{vmatrix}\hat{i} &\hat{j} &\hat{k} \\x &y &z \\1 &1 &\lambda \\\end{vmatrix}=\hat{i}(\lambda y-z)+\hat{j}(z-\lambda x)+\hat{k}(x-y)\end{array} \)
\(\begin{array}{l}\Rightarrow \lambda y-z=13,z-\lambda x=-1,x-y=-4\end{array} \)
and x + y + λz = –21
⇒ clearly, λ = 3, x = –2, y = 2 and z = –7
So,
\(\begin{array}{l}\vec{b}-\vec{a}=3\hat{i}-\hat{j}+10\hat{k}\end{array} \)
and
\(\begin{array}{l}\vec{b}+\vec{a}=-\hat{i}+3\hat{j}-4\hat{k}\end{array} \)
\(\begin{array}{l}\Rightarrow (\vec{b}-\vec{a}).(\hat{k}-\hat{j})+(\vec{b}+\vec{a}).(\hat{i}-\hat{k})=11+3=14\end{array} \)
7. The total number of three-digit numbers, with one digit repeated exactly two times, is ______.
Answer (243)
Sol. C-1 : All digits are non-zero
\(\begin{array}{l}^{9}C_2.2.\frac{3!}{2}=216\end{array} \)
C-2 : One digit is 0
\(\begin{array}{l}0,0,x\Rightarrow ^{9}C_1.1.=9\end{array} \)
\(\begin{array}{l}0,x,x\Rightarrow ^{9}C_1.2.=18\end{array} \)
Total = 216 + 27 = 243
8. Let f(x) = |(x – 1)(x2 – 2x – 3)| + x – 3, x ∈ R. If m and M are, respectively the number of points of local minimum and local maximum of f in the interval (0, 4), then m + M is equal to
Answer (3)
Sol.
f(x) = |(x – 1)(x2 – 2x – 3)| + x – 3
\(\begin{array}{l}f(x)=\left|(x-1)(x+1)(x-3)\right|+(x-3)\end{array} \)
\(\begin{array}{l}f(x)=\left\{\begin{matrix}(x-3)(x^2) &3\leq x\leq 4 \\(x-3)(2-x^2) &1\leq x<3 \\(x-3)(x^2) &0<x<1 \\\end{matrix}\right.\end{array} \)
\(\begin{array}{l}f(x)=\left\{\begin{matrix}3x^2-6x &3<x<4 \\-3x^2+6x+2 &1<x<3 \\3x^2-6x &0<x<1 \\\end{matrix}\right.\end{array} \)
\(\begin{array}{l}f'(3^+)>0 f'(3^-)<0\to Minimum\end{array} \)
\(\begin{array}{l}f'(1^+)>0 ~~f'(1^-)<0\to Minimum\end{array} \)
\(\begin{array}{l}x\in(1,3) f'(x)=0\end{array} \)
at one point → Maximum \(\begin{array}{l}x\in (3,4) f'(x)\neq 0\end{array} \)
\(\begin{array}{l}x\in (0,1) f'(x)\neq 0\end{array} \)
So, 3 points
9. Let the eccentricity of the hyperbola \(\begin{array}{l}\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\end{array} \)
be 5/4. If the equation of the normal at the point (8/√5, 12/5) on the hyperbola is 8√5 x + β y = λ, then λ – β is equal to ____.
Answer (85)
Sol.
\(\begin{array}{l}\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\left(e=\frac{5}{4}\right )\end{array} \)
So,
\(\begin{array}{l}b^2=a^2\left(\frac{25}{16}-1\right)\Rightarrow b=\frac{3}{4}a\end{array} \)
Also, (8/√5, 12/5) lies on the given hyperbola.
So,
\(\begin{array}{l}\frac{64}{5a^2}-\frac{144}{25\left(\frac{9a^2}{16}\right )}=1\Rightarrow a=\frac{8}{5}\ \text{and}\ b=\frac{6}{5}\end{array} \)
Equation of normal
\(\begin{array}{l}\frac{64}{25}\left(\frac{x}{8/\sqrt{5}}\right)+\frac{36}{25}\left(\frac{y}{12/5}\right)=4\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{8}{5\sqrt{5}}x+\frac{3}{5}y=4\end{array} \)
\(\begin{array}{l}\Rightarrow 8\sqrt{5}x+15y=100\end{array} \)
So,
\(\begin{array}{l}\beta=15\ and\ \lambda =100 \end{array} \)
Gives
\(\begin{array}{l}\lambda-\beta =85 \end{array} \)
10. Let l1 be the line in xy-plane with x and y intercepts ⅛ and \(\begin{array}{l}\frac{1}{4\sqrt{2}}\end{array} \)
respectively and l2 be the line in zx-plane with x and z intercepts -⅛ and \(\begin{array}{l}-\frac{1}{6\sqrt{3}}\end{array} \)
respectively. If d is the shortest distance between the line l1 and l2, then d–2 is equal to __________.
Answer (51)
Sol.
\(\begin{array}{l}\frac{x-\frac{1}{8}}{\frac{1}{8}}=\frac{y}{-\frac{1}{4\sqrt{2}}}=\frac{z}{0}……L_{1}\end{array} \)
or \(\begin{array}{l}\frac{x-\frac{1}{8}}{1}=\frac{y}{-\sqrt{2}}=\frac{z}{0}……..(i)\end{array} \)
Equation of L2
\(\begin{array}{l}\frac{x+\frac{1}{8}}{-6\sqrt{3}}=\frac{y}{0}=\frac{z}{8}………(ii)\end{array} \)
\(\begin{array}{l}d=\left|\frac{(\vec{c}-\vec{a}).(\vec{b}\times \vec{d})}{\left|\vec{b}\times \vec{d}\right|}\right|\end{array} \)
\(\begin{array}{l}=\frac{\left(\frac{1}{4}\hat{i}\right ).(4\sqrt{2}\hat{i}+4\hat{j}+3\sqrt{6}\hat{k})}{\sqrt{(4\sqrt{2})^2+4^2+(3\sqrt{6})^2}}\end{array} \)
\(\begin{array}{l}=\frac{\sqrt{2}}{\sqrt{32+16+54}}=\frac{1}{\sqrt{51}}\end{array} \)
d–2 = 51
JEE Main 2022 Question Paper & Solutions – June 25 Shift 2
JEE Main 2022 June 25 Shift 2 Question Paper – Physics Solutions
JEE Main 2022 June 25 Shift 2 Question Paper – Chemistry Solutions
JEE Main 2022 June 25 Shift 2 Question Paper – Maths Solutions
Frequently Asked Questions – FAQs
Q1
What is the overall difficulty level of JEE Main 2022 June 25 shift 2 Maths question paper?
The overall difficulty level of Maths was 1.62 out of 3. There were 10 easy questions, 9 medium questions and 2 difficult questions as per the memory-based question paper.
Q2
How many questions should the students attempt in the JEE Main 2022 June 25th shift 2 Maths question paper?
Students should attempt 25 questions. There is a total of 30 questions, of which 20 are from section A, and 10 are from section B. Students need to do only 5 out of 10 questions from section B.
Q3
How many questions were asked from Class 11 in JEE Main 2022 June 25 Maths evening shift question paper?
There were 12 questions from Class 11 as per the memory-based question paper.
Q4
What is the difficulty level of questions asked from Statistics?
The questions asked from Statistics were medium level.
Q5
What is the total mark of JEE Main 2022 June 25 Shift 2 Maths Question Paper?
The total mark for JEE Main 2022 June 25 Shift 2 Maths Question Paper is 120.












Comments