Moment of Inertia of Solid Sphere

Inertia is the property of the matter by which it resists any change in the state of rest or state of motion. The larger the inertia of the body, the greater is the force required to make changes in the velocity in the given time interval. Similarly, the moment of inertia is that property of the object to resist any change in the state of rotatory motion. The larger the moment of inertia the larger is the amount of torque required to cause any change in the angular velocity. The torque is the force that causes the object to rotate about an axis.

How to Find Moment of Inertia of Solid Sphere

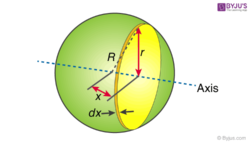
A uniform solid sphere of mass M and radius R is taken. Moment of inertia is calculated about an axis passing through its centre. The solid sphere should be sliced to infinitesimally thin solid cylinders. The moment of inertia of a solid cylinder is given as

I = (½)MR²

For infinitesimally small cylinder moment of inertia can be written as

dI = (½)r²dm

dm = ρ dV,

where ρ is the density of the solid cylinder and dV is the volume.

dV = πr²dx

Putting the value of dV in dm

dm = ρπr²dx

Substituting dm into dI

dI = (½)ρπr⁴dx

In the above image r, x and R form a triangle. Hence, by using Pythagoras theorem we have

r² = R² – x²

Substituting in the equation for dI

dI = (½)ρπ(R² – x²)²dx

Integrating between -R and R

Simplifying the above equation we get

I = (½)ρπ(16/15)R⁵

The density of the sphere, ρ = M/V

ρ = M/[(4/3)πR³]

Substituting ρ in the equation of I, we will have

I = ((½) x M/[(4/3)πR³] x π(16/15)R⁵

I = (2/5)MR²

Moment of inertia of solid sphere, I = (2/5)MR²

Parallel Axis Theorem