The Pauli Exclusion Principle is one of the important principles, along with the Aufbau Principle and Hund’s Rule in Chemistry. Learning about it is crucial for students, especially when they are studying about electrons. The Pauli exclusion principle basically helps us to understand the electron arrangements in atoms and molecules, and it also gives an explanation for the classification of elements in the periodic table. In this section, we will study the Pauli exclusion principle in detail and learn about all the underlying concepts.
What Is the Pauli Exclusion Principle?
The Pauli exclusion principle states that in a single atom, no two electrons will have an identical set or the same quantum numbers (n, l, ml, and ms). To put it in simple terms, every electron should have or be in its own unique state (singlet state). There are two salient rules that the Pauli exclusion principle follows:
- Only two electrons can occupy the same orbital.
- The two electrons that are present in the same orbital must have opposite spins, or they should be antiparallel.
However, the Pauli exclusion principle does not only apply to electrons, it applies to other particles of half-integer spin, such as fermions. It is not relevant for particles with an integer spin, such as bosons which have symmetric wave functions. Moreover, bosons can share or have the same quantum states, unlike fermions. As far as the nomenclature goes, fermions are named after the Fermi–Dirac statistical distribution that they follow. Bosons, on the other hand, get their name from the Bose-Einstein distribution function.
Formulation of the Principle
An Austrian physicist named Wolfgang Pauli formulated the principle in the year 1925. With this principle, he basically described the behaviour of the electrons. Later in the year 1940, he expanded on the principle to cover all fermions under his spin-statistics theorem. Besides, fermions that are described by the principle include elementary particles such as quarks, electrons, neutrinos, and baryons.
Wolfgang Pauli was awarded the Nobel Prize in the year 1945 for the discovery of the Pauli exclusion principle and his overall contribution to the field of quantum mechanics. He was nominated by Albert Einstein for the award.
Pauli Exclusion Principle in Chemistry
In Chemistry, the law is mainly used to explain or determine the electron shell structure of atoms and predict which atoms are likely to donate electrons. How does the principle work, or where does it apply? Well, if we look at the atoms, whenever it gains a new electron or electrons, it usually moves to the lowest energy state or shifts to the outermost shell. If the state has one electron, then it can either spin up or spin down. Now, if we consider the Pauli exclusion principle, if there are two electrons in a state, then each of the electrons will have a spinup or spin downstate but not the same.
Pauli Exclusion Principle Example
We can take a neutral helium atom as a common Pauli exclusion principle example. The atom has 2 bound electrons, and they occupy the outermost shell with opposite spins. Here, we will find that the two electrons are in the 1s subshell where n = 1, l = 0, and ml = 0.
Their spin moments will also be different. One will be ms = -1/2, and the other will be +1/2. If we draw a diagram, then the subshell of the helium atom will be represented with 1 “up” electron and 1 “down” electron. In essence, 1s subshell consists of two electrons, which have opposite spins.
Similarly, if we take hydrogen, it will have 1s subshell with 1 “up” electron (1s1). Lithium will have the helium core (1s2) and then one more “up” electron ( 2s1). What we are trying to depict here is that the electron configuration of the orbitals is written in the following manner.
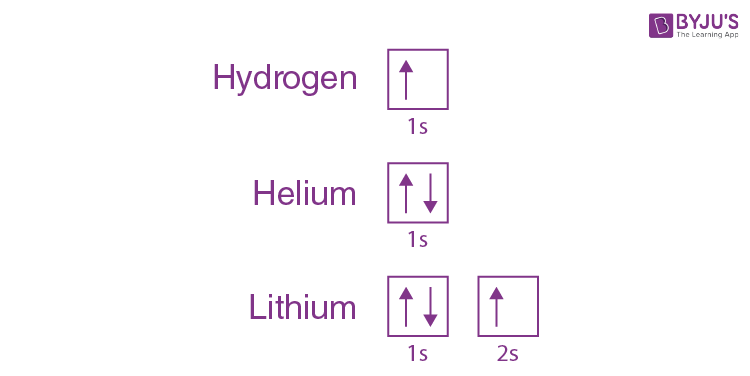
Formulation of the Pauli Exclusion Principle
From the above example, we can further deduce that successive larger elements will have shells of successively higher energy. The number of electrons in the outermost shell is also directly related to the different chemical properties that elements possess. Elements with the same number of electrons in the outermost shell will have similar properties.
Nuclear Stability and Pauli Exclusion Principle
The nuclei in an atom consist of neutrons and protons, which are held together by the nuclear force. However, protons tend to repel each other via electromagnetic force as a result of their positive charge. Basically, these two forces are working against (competing) each other, thereby leading to the stability of nuclei. Meanwhile, you will find only certain sets or combinations of protons and neutrons that form stable nuclei. The nucleus is mostly stabilised by the neutrons as they attract each other and protons. This further helps counterbalance the electrical repulsion between protons. When this happens, the number of protons goes up. In essence, an increasing ratio of neutrons to protons is needed to form a stable nucleus.
In case there are a larger number of (neutrons also obey the Pauli exclusion principle) or too few neutrons for a given number of protons, the nucleus of the atom is not stable. This will lead to radioactive decay. In addition, Pauli exclusion principle also has an effect on the critical energy of fissile and fissionable nuclei. For example, if we look at actinides that have an odd neutron number, they are usually fissile or, in other words, fissionable with slow neutrons. On the other hand, actinides that have even neutron numbers are usually not fissile, or we can say that they are fissionable with fast neutrons. Similarly, due to the Pauli exclusion principle, heavy nuclei with an even number of protons and neutrons are very stable due to the presence of ‘paired spin’. Alternatively, nuclei with an odd number are unstable.
Importance and Applications of Pauli Exclusion Principle
- The Pauli exclusion principle helps to explain a wide variety of physical phenomena, such as the electron shell structure of atoms and the way atoms share electrons.
- It helps in describing the various chemical elements and how they participate in forming chemical bonds.
- The periodic table can also be defined with the help of this principle.
- Solid-state properties: Many electrical, optical, magnetic, mechanical and chemical properties of solids are the direct consequence of Pauli exclusion.
- The principle helps in describing the stability of large systems with many electrons and many nucleons.
- Apart from Chemistry, the principle is a fundamental principle in quantum mechanics which is mainly studied in Physics.
- It is also used in astrophysics.
Key Points
Here, we have summarised and listed out some important points from the lesson. Students should keep these points in mind while studying this topic.
- Electrons are part of subatomic particles called fermions.
- Fermions are particles with half-integer spin.
- All fermions, including neutrons and protons (derived particles), obey the Pauli exclusion principle.
- Pauli exclusion principle states that no two identical electrons (fermions) can have the same quantum state.
- Bosons, which have integer values of spin, do not obey the Pauli exclusion principle. Photons, gravitons, gluons are an example of bosons.
Introduction to Quantum Numbers
Every electron in an atom can be defined completely by quantum numbers. Quantum numbers are values that describe the state of an electron, such as the electron shell, the shape of the orbital, the orientation and the number of orbitals and the electronic spin. There are four quantum numbers that are used.
- n is the principal quantum number. It talks about the position of the electron in the innermost shell.
- l is said to be the orbital angular momentum quantum number and helps us determine the shape of an orbital.
- ml is expressed as the magnetic quantum number, and it reveals the number of orbitals and their orientation.
- ms denotes the spin quantum number, and it identifies the direction of the electron spin.
Frequently Asked Questions (FAQs)
What are the four sets of quantum numbers, and what is their significance?
Principal quantum number (n) – It signifies the size of the atomic orbital
Azimuthal quantum number (l) – It signifies the shape of the atomic orbital
Magnetic quantum number (ml) – It signifies the orientation of atomic orbitals in space.
Spin quantum number (ms) – It signifies the electron’s spin in the atomic orbital.

Comments