A plane curve that is mirror-symmetrical, U-shaped and points set where they are equidistant from the fixed line is called directrix, and a fixed point is called focus a parabola. y2 = 4ax represents the equation of the parabola, given the directrix is parallel to the y-axis. Similarly, x2 = 4ay is the equation of the parabola when the directrix is parallel to the x-axis. The latus rectum of the parabola is a line (named chord) that is found to be parallel to the directrix and pass through the focus. The parametric coordinates of a parabola are given by x = at2 and y = 2at. The line (named chord) that passes through the fixed chord and focus of the parabola is termed the focal chord.
How to Find the Position of a Point with Respect to a Parabola
An open and unbounded figure is a parabola. In the given plane, it is split into 3 disjoint parts, namely
a) Inside the parabola: The region in which the focus of a parabola is included constitutes the inside of the parabola. Any point present here is called the interior point.
b) On the parabola: The boundary of the parabola is called the region on the parabola.
c) Outside the parabola: The remaining region in which the focus is absent is called the outside of the parabola. Any point present here is called the exterior point.
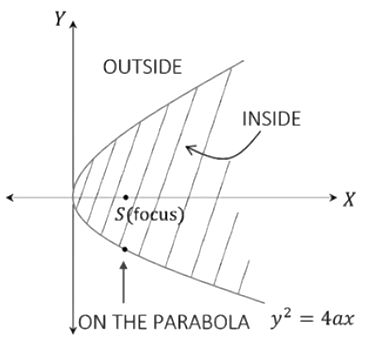
The condition to conclude the position of a point with respect to the parabola is given below.
Consider the parabola y2 = 4ax, a > 0.
Let P (x1, y1) be a point in
Case 1) Inside the parabola.
2) On the parabola.
3) Outside the parabola.
Case 1) When the point is inside the parabola.
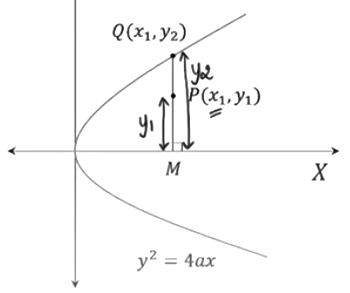
Draw a perpendicular to the x-axis such that it splits the parabola at point Q. Let Q be (x1, y2). Since Q is on the parabola, it will satisfy the equation.
y22 = 4ax1
Because P is present inside the parabola, y1 < y22
y12 < 4ax1
y12 – 4ax1 < 0
Case 2) When P (x1, y1 ) lies on the parabola.
y12 = 4ax1
y12 – 4ax1 = 0
Case 3) When P (x1, y1) lies outside the parabola.
Generate a point that lies inside the parabola. Draw a perpendicular from P to the x-axis, such that it meets the parabola at a point Q (x1, y2). Since Q is on the parabola, it will satisfy its equation.
y22 = 4ax1
Compare the lengths of perpendicular from P and Q onto the x-axis.
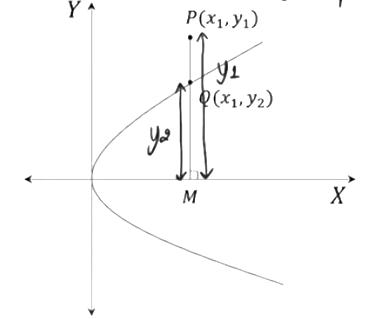
y12 > y22
y12 > 4ax1
y12 – 4ax1 > 0
Solved Examples
Example 1: Find the position of the point (10, 5) with respect to the parabola x2 = 16y.
Solution:
The point (10, 5) with respect to the parabola x2 = 16y.
x2 – 16y = 0
⇒ (10)2 – 16 × 5 = 0
100 – 80 = 20 > 0
It is positive.
The point (10, 5) lies outside the parabola.
Example 2: Find the position (interior or exterior or on) of the following points with respect to the parabola y2 = 6x.
(i) (6, –6)
(ii) (2, 3)
Solution:
y2 = 6x is the equation of the parabola.
S = y2 – 6x
i) S = (- 6)2 – 6 * 6 = 36 – 36 = 0
(6, – 6) lies on the parabola.
ii) (2, 3)
S = 32 – 6 . 2 = 9 – 12 = – 3 < 0
(2, 3) lies inside the parabola.
Position of a Point with Respect to a Parabola

Position of a Point with Respect to Hyperbola

Frequently Asked Questions
What is the condition that point P(x1, y1) lies inside the parabola y2 = 4ax?
If y12-4ax1<0, the point P(x1, y1) lies inside the parabola y2 = 4ax.
What is the standard equation of a parabola?
If the directrix is parallel to the y-axis, then the standard equation of a parabola is given by y2 = 4ax. Here, a is the distance from the origin to the focus.
What is the condition that point P(x1, y1) lies outside the parabola y2 = 4ax?
If y12-4ax1 > 0, the point P(x1, y1) lies outside the parabola y2 = 4ax.
What is the eccentricity of a parabola?
The eccentricity of the parabola is equal to 1.
What is the condition that point P(x1, y1) lies on the parabola y2 = 4ax?
If y12-4ax1 = 0, the point P(x1, y1) lies on the parabola y2 = 4ax.
Comments