A quadratic inequality is simply a type of equation which does not have an equal sign and includes the highest degree two. The wavy curve method is a method used to solve quadratic inequalities. Solving quadratic inequalities is the same as solving quadratic equations. We just have to keep in mind some tips and tricks while attempting more complicated inequalities. We will learn shortcuts to solve different quadratic inequalities here.

The wavy curve method is explained below.

Wavy Curve Method or Methods of Intervals

The wavy curve method or the methods of intervals is helpful in solving inequalities of the form:

Steps for Solving Quadratic Inequalities

Step 1: Consider the given polynomial equation and find all the roots of the given polynomial equation F (x) and G (x).

i.e.

Where α₁, α₂, α₃,…, α_n are roots of F (x) and β₁, β₂, β₃,…., β_m are roots of polynomial equation G (x).

Note: H (x) = 0 for x = α₁, α₂, α₃,…, α_n and H (x) is not defined for x = β₁, β₂, β₃,…., β_n

Step 2: Compare the roots of both F (x) and G (x) and arrange all the roots of F (x) and G (x) in increasing order, say a₁, a₂, a₃,…., a_m+n.

Step 3: Plot them on the number line. Now, draw a wavy curve starting from the right of a_{m + n} along the number line that alternatively changes its position at these points.

Note: H (x) is a positive function for all the intervals in which the curve lies above the number line, and H (x) is a negative function for all the intervals in which the curve lies below the number line.

Note: All the zeros of the given polynomial equation H (x) must be marked with coloured black circles on the number line, whereas all points of discontinuities of the function H (x) must be marked on the number line with white circles.

Shortcut Tips for Solving Quadratic Inequalities

If ax² + bx + c > 0 and (a ≠ 0):

Case 1: (i) If D (b² – 4ac) > 0, i.e., the quadratic equation f (x) has two different roots and a < b.

If a > 0, then

And, if a < 0, then, x ∈ (α, β)

Case 2: If D (b² – 4ac) = 0, i.e., the quadratic equation f (x) has equal roots, i.e., a = b.

If a > 0, then,

And, if a < 0, then x ∈ Ø

Case 3: If D (b² – 4ac) < 0, i.e., the quadratic equation has imaginary roots.

If a > 0, then

And, if a < 0 then, x ∈ Ø

In general, if (x – a) (x – b) ≥ 0, then a ≤ x ≤ b,

(x – a) (x – b) ≤ 0 and a < b, then a ≤ x or x ≥ b.

Hence, the quadratic inequalities can be quickly solved using the method of intervals.

Solution of the Inequality

(a) Write all the terms present in the inequality as their linear factors in standard form, i.e., x + a.

(b) If the inequality contains quadratic expression, f(x) = ax² + bx + c, then first check the discriminant (D = b² – 4ac).

(i) If D > 0, then the expression can be written as f(x) = a (x – α)(x – β), where α and β are given by

(ii) If D = 0, then the expression can be written as

(iii) If D > 0 & if

• A > 0, then f(x) > 0 ∀ x ∈ R, and the expression will be cross multiplied, and the sign of the inequality will not change.
• A < 0, then f(x) < 0 ∀ x ∈ R, and the expression will be cross multiplied, and the sign of the inequality will change.
• If the expression (say ‘f’) is cancelled from the same side of the inequality, then cancel it and write f ≠ 0. For example,

(i)

(ii)

Types of Inequalities

Type I: Inequalities involving non-repeating linear factors

1^st condition

2^nd condition

Illustration: 

Sol:

Comparing all brackets separately with 0, we can find the range of values for x.

Type II: Inequalities involving repeating linear factors

Type III: Inequalities expressed in rational form

Illustration:

Sol: If

Hence, x ≠ –3, 4 and x = 1, –2;     

Illustration:

Sol: Similar to the illustration above.

Illustration:

Sol: First, reduce the given inequalities in rational form and then solve it in the manner similar to the illustration above.

Type IV: Double inequality

Illustration 

Sol: Here, 3x² – 7x + 8 > x² + 1 therefore if D < 0 & if a > 0, then f(x) > 0 and always positive for all real x.

3x² – 7x + 8 > x² + 1 or 2x² – 7x + 7 > 0

D = b² – 4ac = 49 – 56 = –7

3x² – 7x + 8 < 2x² + 2 or x² – 7x + 6 < 0 Þ

Type V: Inequalities involving biquadrate expression

Illustration 

Sol: Using x² + 3x = y, we can solve this problem

Let x² + 3x = y                                    

y² – 2y – 8 > 0                        

Some Basic Properties of Inequality

Intervals

Given E(x) = (x – a)(x – b)(x – c)(x – d) > 0

To find the solution set of the above inequality, we have to check the intervals in which E(x) is greater/less than zero.

• Closed interval: The set of all values of x, which lies between a and b and is also equal to a and b, is known as a closed interval, i.e., if a < x < b, then it is denoted by x ϵ [a, b].
• Open-closed interval: The set of all values of x, which lies between a and b, equal to b, but not equal to a, is known as an open-closed interval, i.e., if a < x < b, then it is denoted by x ϵ (a, b).
• Open-closed interval: The set of all values of x, which lies between a and b, equal to b, but not equal to a, is known as an open-closed interval, i.e., if a < x < b, then it is denoted by x ϵ (a, b].
• Closed-open interval: The set of all values of x, which lies between a and b, equal to a but not equal to b, is called a closed-open interval, i.e., if a < x < b, then it is denoted by c ϵ [a, b).

Note:

Properties

(a) In an inequality, any number can be added or subtracted from both sides of the inequality.

(b) Terms can be shifted from one side to the other side of the inequality. The sign of inequality does not change.

(c) If we multiply both sides of the inequality by a non-zero positive number, then the sign of inequality does not change.

But if we multiply both sides of the inequality by a non-zero negative number, then the sign of the inequality does get changed.

(d) In the inequality, if the sign of an expression is not known, then it cannot be cross-multiplied. Similarly, without

knowing the sign of an expression, a division is not possible.

(i)

(ii)

Also, Practise:

JEE Previous Year Questions on Quadratic Equations 

Solved Examples

Example 1: Let

Solution:

On arranging the roots of the given polynomial equation in increasing order [-2, -1, +3, +7] and plotting them on the number line,

P (x) is positive, i.e., P (x) > 0, then

P (x) is negative, i.e., P (x) < 0, then

Example 2: Solve the given quadratic in equation:

Solution:

Given,

i.e.

Or,

Or,

Or,

Neglecting x² + 1 as x ∈ R.

Therefore, x ∈ [1, 6]

Example 3: Solve the given quadratic in equation:

Solution:

From the given quadratic inequality, x can’t be 2, – 2, 0.

The given quadratic inequality can be rewritten as:

i.e.,

Or,

Or,

Or,

Using quadratic formula:

i.e.,

Or,

On arranging the roots of the given polynomial equation in increasing order and plotting them on the number line,

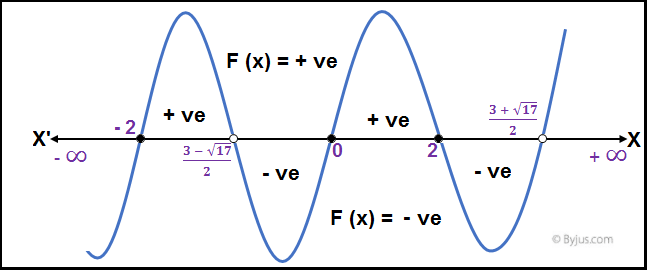
Therefore, from the above graph:

Modulus Inequalities – Wavy Curve Method

1,835

Graphs & Types of Modulus Functions

2,261

Solving Modulus Inequalities

1,737

Fundamental Properties – Inequalities

20,469

Inequalities – Wavy Curve Method

2,44,790