Trigonometry is one of the important branches of mathematics that studies triangles and their measurements. In this article, you will learn trigonometric ratios, graphs of trigonometric functions, identities, maximum and minimum values, main formulas and much more.
Trigonometric Ratios
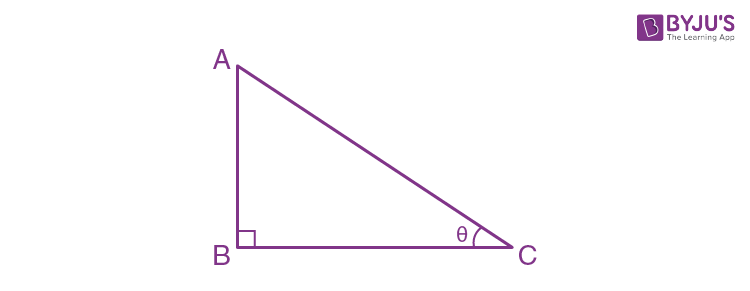
\(\begin{array}{l}\sin \theta =\frac{AB}{AC}=\frac{opp}{hyp}\end{array} \)
\(\begin{array}{l}\cos \theta =\frac{BC}{AC}=\frac{adj}{hyp}\end{array} \)
\(\begin{array}{l}\tan \theta =\frac{AB}{BC}=\frac{opp}{adj}\end{array} \)
\(\begin{array}{l}\cot\theta =\frac{BC}{AB}\end{array} \)
\(\begin{array}{l}\sec\theta =\frac{AC}{BC}\end{array} \)
\(\begin{array}{l}\cos ec\theta =\frac{AC}{AB}\end{array} \)
Trigonometric Circular Function
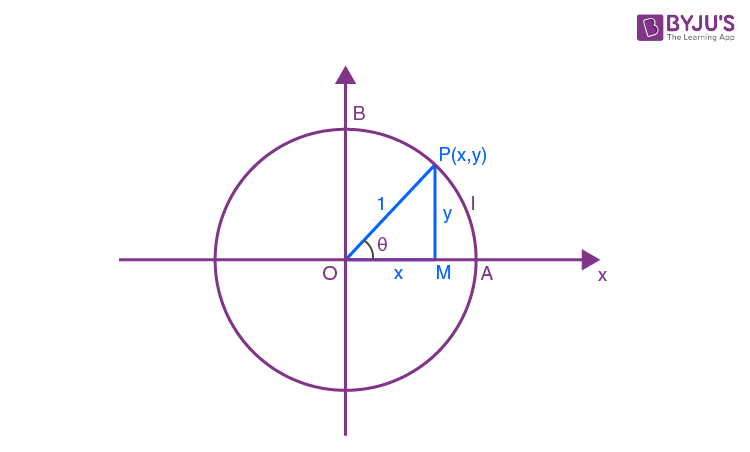
\(\begin{array}{l}<AOP=\frac{arcAP}{r}=\frac{l}{r}\end{array} \)
cos θ = x
sin θ = y
\(\begin{array}{l}\tan\theta=\frac{x}{y}\end{array} \)
Graphs of T Ratios
y = sin x
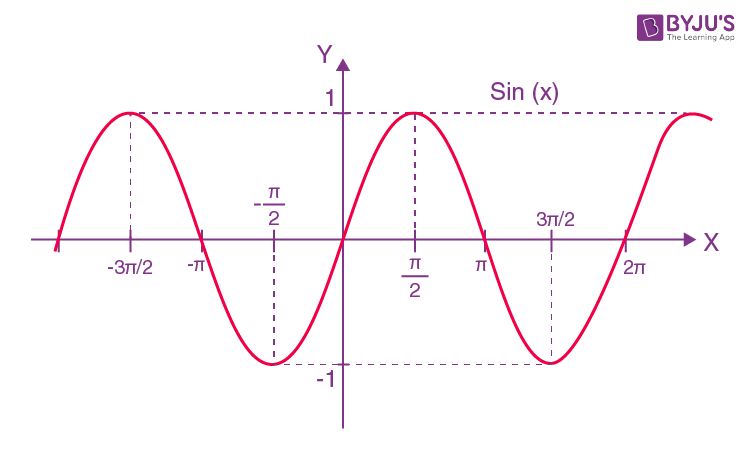
Domain R
Range (-1,1)
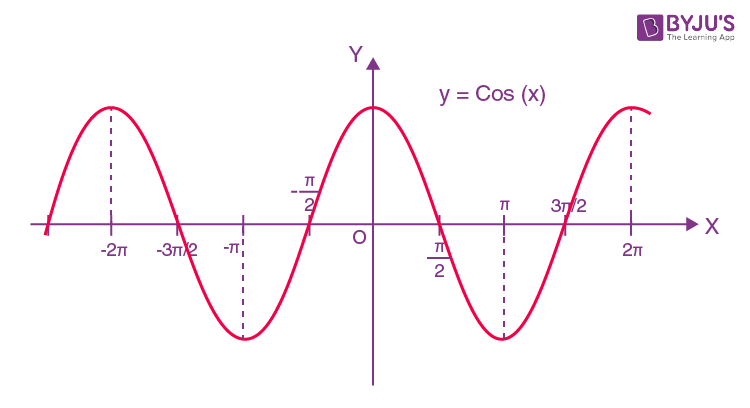
y = cos x
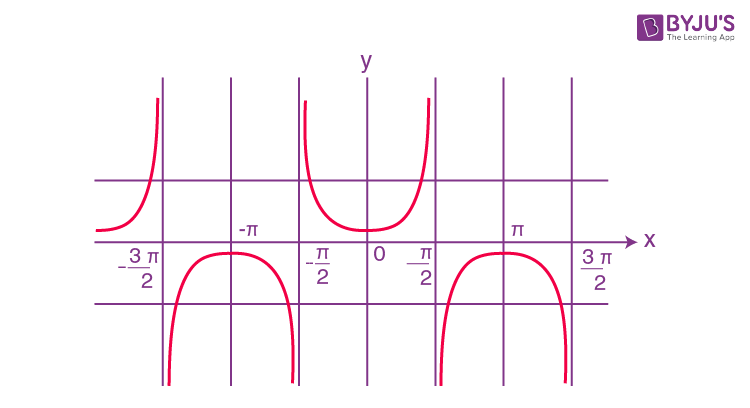
y = tan x
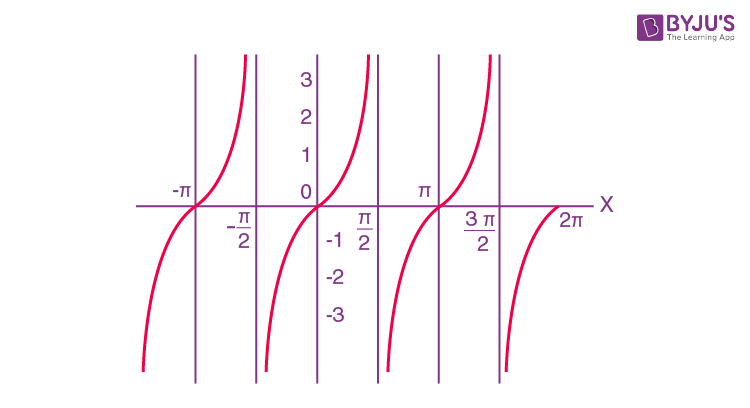
y = cot x
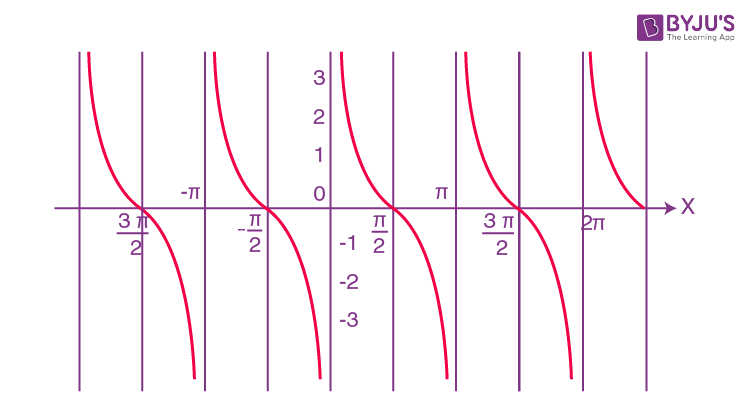
\(\begin{array}{l}y=\sec x,\end{array} \)
\(\begin{array}{l}Domain:\,\,\,\,\,R-\left\{ (2x+1)\,\frac{\pi }{2} \right\}\end{array} \)
and
\(\begin{array}{l}Range:\,(-\infty -1)\, \cup \,(1,\infty )\end{array} \)
y = cosec x
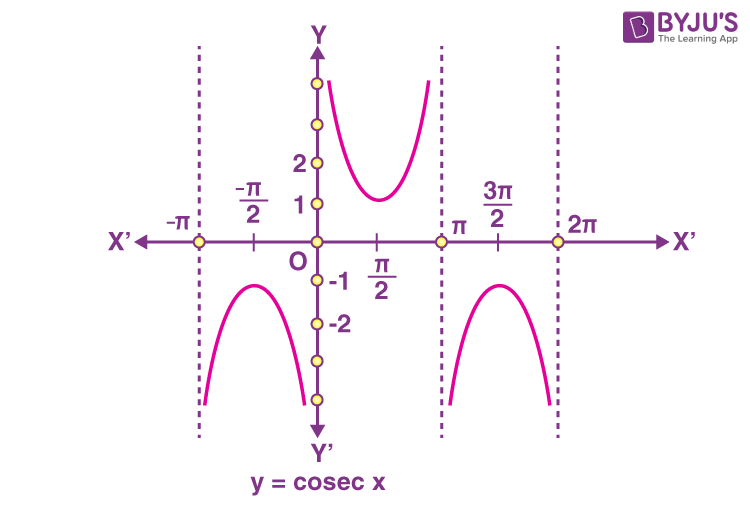
\(\begin{array}{l}Domain:\,R-\{n\pi \}\end{array} \)
and
\(\begin{array}{l}Range:\,(-\infty -1)\, \cup \,(1,\infty )\end{array} \)
Also Read:
Trigonometric Equations and Its Solutions
Trigonometry JEE Main Previous Year Questions
Inverse Trig JEE Main Previous Year Questions
Trignometric Identities
\(\begin{array}{l}{{\sin }^{2 }\theta}+{{\cos }^{2 }\theta}=1\end{array} \)
\(\begin{array}{l}1+{{\tan }^{2 }\theta}=\,{{\sec }^{2 }\theta}\end{array} \)
\(\begin{array}{l}1+{{\cot }^{2 }\theta}=\cos e{{c}^{2 }\theta}\end{array} \)
\(\begin{array}{l}\sin ^{4}\theta +\cos^{4}=1-2\sin ^{2 }\theta\cos ^{2 }\theta\end{array} \)
\(\begin{array}{l}{{\sin }^{6}}\theta +{{\cos }^{6}}=1-3{{\sin }^{2 }\theta}{{\cos }^{2 }\theta}\end{array} \)
Remember:
\(\begin{array}{l}\sec \theta -\tan \theta =\frac{1}{\sec \theta +\tan \theta }\end{array} \)
and
\(\begin{array}{l}cosec\theta -\cot \theta =\frac{1}{cosec\theta +\cot \theta }\end{array} \)
T-Ratio at Some Standard Angles
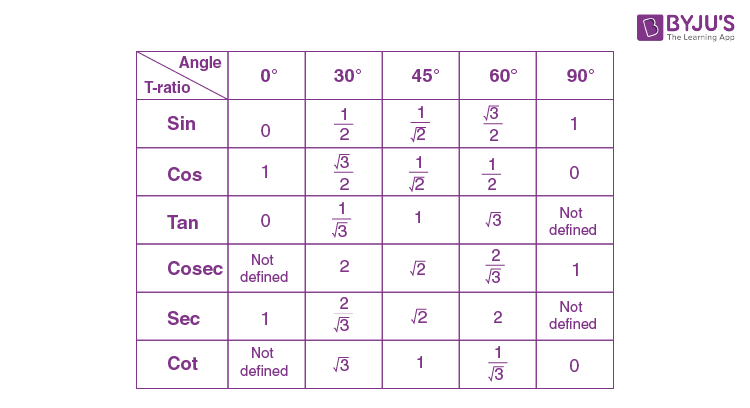
T-Ratio at Some Specific Angles
T-ratio
|
\(\begin{array}{l}7\frac{1{}^\circ }{2}\end{array} \) |
15o |
\(\begin{array}{l}22\frac{1{}^\circ }{2}\end{array} \) |
18o |
\(\begin{array}{l}\sin\theta\end{array} \) |
\(\begin{array}{l}\frac{\sqrt{4-\sqrt{2}-\sqrt{6}}}{2\sqrt{2}}\end{array} \) |
\(\begin{array}{l}\frac{\sqrt{3}-1}{2\sqrt{2}}\end{array} \) |
\(\begin{array}{l}\frac{1}{2}\sqrt{2-\sqrt{2}}\end{array} \) |
\(\begin{array}{l}\frac{\sqrt{5-1}}{4}\end{array} \) |
\(\begin{array}{l}\cos\theta\end{array} \) |
\(\begin{array}{l}\frac{\sqrt{4+\sqrt{2}+\sqrt{6}}}{2\sqrt{2}}\end{array} \) |
\(\begin{array}{l}\frac{\sqrt{3}+1}{2\sqrt{2}}\end{array} \) |
\(\begin{array}{l}\frac{1}{2}\sqrt{2+\sqrt{2}}\end{array} \) |
\(\begin{array}{l}\frac{1}{4}\sqrt{10+2\sqrt{5}}\end{array} \) |
\(\begin{array}{l}\tan\theta\end{array} \) |
\(\begin{array}{l}\left( \sqrt{3}-\sqrt{2} \right)\left( \sqrt{2}-1 \right)\end{array} \) |
\(\begin{array}{l}2-\sqrt{3}\end{array} \) |
\(\begin{array}{l}\sqrt{2-1}\end{array} \) |
\(\begin{array}{l}\frac{\sqrt{25+10\sqrt{15}}}{5}\end{array} \) |
Maximum and Minimum Value of Standard Trigonometric Expressions
- Maximum value of
\(\begin{array}{l}a\cos \theta \pm b\sin \theta =\sqrt{{{a}^{2}}+{{b}^{2}}}\end{array} \)
- Minimum value of
\(\begin{array}{l}a\cos \theta \pm b\sin \theta =-\sqrt{{{a}^{2}}+{{b}^{2}}}\end{array} \)
- Maximum value of
\(\begin{array}{l}a\cos \theta \pm b\sin \theta +c=c+\sqrt{{{a}^{2}}+{{b}^{2}}}\end{array} \)
- Minimum value of
\(\begin{array}{l}a\cos \theta \pm b\sin \theta +c=c-\sqrt{{{a}^{2}}+{{b}^{2}}}\end{array} \)
Problems on Trigonometry
Example 1: If
\(\begin{array}{l}{{\sec }^{4}}x-{{{cosec}}^{4}}x-2{{\sec }^{2}}x+2\cos e{{c}^{2}}x=\frac{15}{4}\end{array} \)
. Find tan x.
Solution:
\(\begin{array}{l}\left( {{\sec }^{4}}x-2{{\sec }^{2}}x \right)-\left( \cos e{{c}^{4}}x-2\cos e{{c}^{2}}x \right)=\frac{15}{4}\end{array} \)
or
\(\begin{array}{l}\left( {{\sec }^{4}}x-2{{\sec }^{2}}x+1 \right)-\left( \cos e{{c}^{4}}x-2\cos e{{c}^{2}}x+1 \right)=\frac{15}{4}\end{array} \)
\(\begin{array}{l}{{\left( {{\sec }^{2}}x-1 \right)}^{2}}-{{\left( \cos e{{c}^{2}}x-1 \right)}^{2}}=\frac{15}{4}\end{array} \)
\(\begin{array}{l}{{\left( {{\tan }^{2}}x \right)}^{2}}-{{\left( {{\cot }^{2}}x \right)}^{2}}=\frac{15}{4}\end{array} \)
\(\begin{array}{l}{{\tan }^{4}}x-\frac{1}{{{\tan }^{4}}x}=\frac{15}{4}\end{array} \)
\(\begin{array}{l}{{\tan }^{4}}x-\frac{1}{{{tan }^{4}}x}=4-\frac{1}{4}\end{array} \)
On comparing,
\(\begin{array}{l}{{\tan }^{4}}x=4\end{array} \)
\(\begin{array}{l}{{\tan }^{2}}x=2\end{array} \)
\(\begin{array}{l}tan x=\pm \sqrt{2}\end{array} \)
Example 2:
If sin θ, cos θ, and tan θ are in G.P., then
\(\begin{array}{l}{{\cos }^{9}}\theta +{{\cos }^{6}}\theta +3{{\cos }^{3}}\theta {{\cos }^{2}}\theta -1=?\end{array} \)
Solution:
\(\begin{array}{l}\sin \theta .tan\theta =co{{s}^{2}}\theta\end{array} \)
\(\begin{array}{l}{{\sin }^{2}}\theta ={{\cos }^{3}}\theta\end{array} \)
Now,
\(\begin{array}{l}{{\left( {{\cos }^{3}}\theta \right)}^{3}}+{{\left( {{\cos }^{3}}\theta \right)}^{2}}+3{{\cos }^{3}}\theta {{\cos }^{2}}\theta -1\end{array} \)
\(\begin{array}{l}={{\sin }^{6}}\theta +{{\sin }^{4}}\theta +3{{\sin }^{2}}\theta {{\cos }^{2}}\theta -1\end{array} \)
\(\begin{array}{l}={{\sin }^{6}}\theta +{{\sin }^{4}}\theta -\left( 1-3{{\sin }^{2}}\theta {{\cos }^{2}}\theta \right)\end{array} \)
\(\begin{array}{l}={{\sin }^{6}}\theta +{{\sin }^{4}}\theta -\left( {{\sin }^{6}}\theta +{{\cos }^{6}}\theta \right)\end{array} \)
\(\begin{array}{l}={{\sin }^{4}}\theta -{{\cos }^{6}}\theta\end{array} \)
\(\begin{array}{l}={{\sin }^{4}}\theta -{{\left( {{\cos }^{3}}\theta \right)}^{2}}\end{array} \)
\(\begin{array}{l}={{\sin }^{4}}\theta -{{\sin }^{4}}\theta =0\end{array} \)
Example 3:
If sec x – tan x = P, then sec x = ?
Solution:
Given: sec x – tan x = P ….(1)
We know,
\(\begin{array}{l}\sec x-\tan x=\frac{1}{\sec x+\tan x}\end{array} \)
or
\(\begin{array}{l}\sec x\;+\;tan x=\frac{1}{P}….(2)\end{array} \)
Adding (1) and (2)
\(\begin{array}{l}{2\sec x=P+\frac{1}{P}}\end{array} \)
or
\(\begin{array}{l}\sec x=\frac{{{P}^{2}}+1}{2P}\end{array} \)
Example 4:
Prove that
\(\begin{array}{l}\sin \left( -420 \right).\cos \left( 390 \right)+\cos \left( -660 \right)\sin \left( 330 \right)=-1\end{array} \)
Solution:
\(\begin{array}{l}-\sin \left( 420 \right)\cos \left( 390 \right)+\cos \left( 660 \right)\sin 330\end{array} \)
\(\begin{array}{l}=-\sin \left( 2\pi +60 \right)\cos \left( 2\pi +30 \right)+\cos \left( 4\pi -60 \right)\sin \left( 2\pi -30 \right)\end{array} \)
\(\begin{array}{l}=-\sin 60\cos 30+\cos 60\left( -\sin 30 \right)\end{array} \)
\(\begin{array}{l}=-\frac{\sqrt{3}}{2}.\frac{\sqrt{3}}{2}-\frac{1}{2}.\frac{1}{2}\end{array} \)
\(\begin{array}{l}=-\frac{3}{4}-\frac{1}{4}=-\frac{4}{4}=-1.\end{array} \)
Hence proved.
Trigonometric Ratios of Compound Angles
The algebraic sum of two or more angles is generally called compound angles, and angles are known as constituent angles.
Some Important Results
\(\begin{array}{l}\sin \left( A\pm B \right)=\sin A\cos B\pm \cos \,A\,sin\,B\end{array} \)
\(\begin{array}{l}\cos \left( A\pm B \right)=\cos A\cos B\mp \sin \,A\,sin\,B\end{array} \)
\(\begin{array}{l}\tan \left( A\pm B \right)=\frac{\tan A\pm \tan B}{1\tan A\tan \,B}\end{array} \)
\(\begin{array}{l}\cot \left( A\pm B \right)=\frac{\cot A\cot B\mp 1}{\cot B\pm \cot A}\end{array} \)
\(\begin{array}{l}\sin \left( A+B \right)\sin \left( A-B \right)={{\sin }^{2}}A-{{\sin }^{2}}B={{\cos }^{2}}B-{{\cos }^{2}}A\end{array} \)
\(\begin{array}{l}\cos \left( A+B \right)\cos \left( A-B \right)={{\cos }^{2}}A-{{\sin }^{2}}B={{\cos }^{2}}B-{{\sin }^{2}}A\end{array} \)
\(\begin{array}{l}\sin \left( A+B+C \right)=\sin A\cos B\cos C+\sin B\cos A\cos C+\sin C\cos A\cos B-\sin A\sin B\sin C\end{array} \)
\(\begin{array}{l}\cos \left( A+B+C \right)=\cos A\cos B\cos C-\cos A\sin B\sin C-\cos B\sin A\sin C-\cos C\sin A\sin B\end{array} \)
\(\begin{array}{l}\tan \left( A+B+C \right)=\frac{\tan A+\tan B+\tan C-\tan A\tan B\tan C}{1-\tan A\tan B-\tan B\tan C-\tan C\tan A}\end{array} \)
Remember
If A+B+C = 0, then
\(\begin{array}{l}\tan A+\tan B+\tan C=\tan A\tan B\tan C\end{array} \)
Let us solve some problems to understand the concept in a better way.
Example 1
\(\begin{array}{l}\text{If}\ \sin \alpha =\frac{3}{5}\And \cos \beta =\frac{9}{41}\alpha ,\beta \in I\ \text{quadrant}.\end{array} \)
Find sin(α – β).
Solution
\(\begin{array}{l}\sin \alpha =\frac{3}{5}\end{array} \)
\(\begin{array}{l}{{\sin }^{2}}\alpha +{{\cos }^{2}}\alpha =1\end{array} \)
\(\begin{array}{l}{{\cos }^{2}}\alpha =1-\frac{9}{25}=\frac{16}{25}\end{array} \)
\(\begin{array}{l}\cos \alpha =\frac{4}{5},\frac{-4}{5}\end{array} \)
as in first quadrant.
\(\begin{array}{l}\cos \beta =\frac{9}{41}\end{array} \)
\(\begin{array}{l}{{\cos }^{2}}\beta +{{\sin }^{2}}\beta =1\end{array} \)
\(\begin{array}{l}{{\sin }^{2}}\beta =1-\frac{81}{1681}=\frac{1600}{1681}\end{array} \)
\(\begin{array}{l}\sin \beta =\frac{40}{41}\end{array} \)
\(\begin{array}{l}\sin \left( \alpha -\beta \right)=\sin \alpha \cos \beta -\cos \alpha \sin \beta\end{array} \)
\(\begin{array}{l}=\frac{3}{5}\times \frac{9}{41}-\frac{4}{5}\times \frac{40}{41}=\frac{27-160}{205}\end{array} \)
\(\begin{array}{l}=\frac{-133}{205}.\end{array} \)
Example 2
\(\begin{array}{l}\text{Find value of}\ \frac{\sin \left( B-C \right)}{\cos B\cos C}+\frac{\sin \left( C-A \right)}{\cos C\cos A}+\frac{\sin \left( A-B \right)}{\cos A\cos B}.\end{array} \)
Solution
\(\begin{array}{l}\frac{\sin B\cos C-\cos B\sin C}{\cos B\cos C}+\frac{\sin C\cos A-\cos C\sin A}{\cos C\cos A}+\frac{\sin A\cos B-\cos A\sin B}{\cos A\cos B}\end{array} \)
\(\begin{array}{l}tan \;B\;-\;tan \;C\;+\;tan C\;-\;tan A\;+\;tan A\;-\;tan\; B = 0\end{array} \)
Transformation Formulae
\(\begin{array}{l}2\sin A\cos B=\sin \left( A+B \right)+\sin \left( A-B \right)\end{array} \)
\(\begin{array}{l}2\sin B\cos A=\sin \left( A+B \right)-\sin \left( A-B \right)\end{array} \)
\(\begin{array}{l}2\cos A\cos B=\cos \left( A+B \right)+\cos \left( A-B \right)\end{array} \)
\(\begin{array}{l}2\sin A\sin B=\cos \left( A-B \right)-\cos \left( A+B \right)\end{array} \)
\(\begin{array}{l}\sin C+\sin D=2\sin \left( \frac{C+D}{2} \right)\cos \left( \frac{C-D}{2} \right)\end{array} \)
\(\begin{array}{l}\sin C-\sin D=2\cos \left( \frac{C+D}{2} \right)\sin \left( \frac{C-D}{2} \right)\end{array} \)
\(\begin{array}{l}\cos C-\cos D=2\cos \left( \frac{C+D}{2} \right)\cos \left( \frac{C-D}{2} \right)\end{array} \)
\(\begin{array}{l}\cos C-\cos D=2\sin \left( \frac{C+D}{2} \right)\sin \left( \frac{D-C}{2} \right)\end{array} \)
T-Ratio of Multiple Angles
\(\begin{array}{l}\sin 2A=2\sin A\cos A=\frac{2\tan A}{1+{{\tan }^{2}}A}\end{array} \)
\(\begin{array}{l}\cos 2A=2{{\cos }^{2}}A-1=1-2{{\sin }^{2}}A=\frac{1-{{\tan }^{2}}A}{1+{{\tan }^{2}}A}={{\cos }^{2}}A-{{\sin }^{2}}A\end{array} \)
\(\begin{array}{l}\tan 2A=\frac{2\tan A}{1-{{\tan }^{2}}A}\end{array} \)
\(\begin{array}{l}\sin 3A=3\sin A-4{{\sin }^{3}}A\end{array} \)
\(\begin{array}{l}\cos 3A=4{{\cos }^{3}}A-3\cos A\end{array} \)
\(\begin{array}{l}\tan 3A=\frac{3\tan A-{{\tan }^{3}}A}{1-3{{\tan }^{2}}A}\end{array} \)
Remember
\(\begin{array}{l}1+\cos 2A=2{{\cos }^{2}}A\end{array} \)
\(\begin{array}{l}1-\cos 2A=2{{\sin }^{2}}A\end{array} \)
\(\begin{array}{l}\frac{1-\cos 2A}{1+\cos 2A}={{\tan }^{2}}A\end{array} \) |
Values of T-Ratios at Some Useful Angles
\(\begin{array}{l}\sin 75{}^\circ =\frac{\sqrt{3}+1}{2\sqrt{2}}=\cos 15{}^\circ\end{array} \)
\(\begin{array}{l}\cos 75{}^\circ =\frac{\sqrt{3}-1}{2\sqrt{2}}=\sin 15{}^\circ\end{array} \)
\(\begin{array}{l}\tan 75{}^\circ =2+\sqrt{3}=\cot 15{}^\circ\end{array} \)
\(\begin{array}{l}\cot 75{}^\circ =2-\sqrt{3}=\tan 15{}^\circ\end{array} \)
\(\begin{array}{l}\sin 9{}^\circ =\frac{\sqrt{3+\sqrt{5}}-\sqrt{5-\sqrt{5}}}{4}=\cos 81{}^\circ\end{array} \)
\(\begin{array}{l}\cos 9{}^\circ =\frac{\sqrt{3+\sqrt{5}}-\sqrt{5-\sqrt{5}}}{4}=\sin 81{}^\circ\end{array} \)
Important Results
\(\begin{array}{l}\sin \theta \sin \left( 60-\theta \right)\sin \left( 60+\theta \right)=\frac{1}{4}\sin 3\theta\end{array} \)
\(\begin{array}{l}\cos \theta \cos \left( 60-\theta \right)\cos \left( 60+\theta \right)=\frac{1}{4}\cos3 \theta\end{array} \)
\(\begin{array}{l}\tan \theta \tan \left( 60-\theta \right)\tan \left( 60+\theta \right)=\tan 3\theta\end{array} \) |
Let’s solve a few more examples
Example 1
\(\begin{array}{l}\text{Find value of}\ \frac{\sin A\sin 2A+\sin 3A\sin 6A+\sin 4A\sin 13A}{2\sin A\cos 2A+sin3Acos6A+sin4Acos13A}.\end{array} \)
Solution
\(\begin{array}{l}\frac{\cos \left( -A \right)-{\cos \left( 3A \right)}+{\cos 3A}-{\cos 9A}+{\cos 9A}-\cos 17A}{{\sin 3A}+\sin \left( -A \right)+{\sin 9A}+{sin\left( -3A \right)}+\sin \left( 17A \right)+{\sin \left( -9A \right)}}\end{array} \)
\(\begin{array}{l}=\frac{\cos A-\cos 17A}{\sin 17A-\sin A}\end{array} \)
\(\begin{array}{l}=\frac{{2}\sin 9A{\sin 8A}}{{2}\cos 9A{\sin 8A}}\end{array} \)
= tan 9A
Example 2
\(\begin{array}{l}{{\sin }^{2}}5{}^\circ +{{\sin }^{2}}10{}^\circ +{{\sin }^{2}}15{}^\circ +……….+{{\sin }^{2}}90{}^\circ =?\end{array} \)
Solution
\(\begin{array}{l}{{\sin }^{2}}5{}^\circ +{{\sin }^{2}}10{}^\circ +……….+{{\sin }^{2}}85{}^\circ +{{\sin }^{2}}90{}^\circ\end{array} \)
\(\begin{array}{l}={{\sin }^{2}}5{}^\circ +{{\sin }^{2}}10{}^\circ +……….+{{\cos }^{2}}5{}^\circ +{{\sin }^{2}}90{}^\circ\end{array} \)
\(\begin{array}{l}=\left( {{\sin }^{2}}5{}^\circ +{{\cos }^{2}}5{}^\circ \right)+………. +{{\sin }^{2}}45{}^\circ+{{\sin }^{2}}90{}^\circ\end{array} \)
= [1 + 1 + … + 1] + (1/√2)2 + 1
\(\begin{array}{l}=8\times 1+1+\frac{1}{2}\end{array} \)
\(\begin{array}{l}=8+1+\frac{1}{2}=9\frac{1}{2}\end{array} \)
Example 3
Prove that
\(\begin{array}{l}\sin \alpha +sin\left( \alpha +\frac{2\pi }{3} \right)+\sin \left( \alpha +\frac{4\pi }{3} \right)=0\end{array} \)
Solution
\(\begin{array}{l}2\sin \left( \frac{2\alpha }{2}+\frac{4\pi }{6} \right)\cos \left( -\frac{4\pi }{6} \right)+\sin \left( \alpha +\frac{2\pi }{3} \right)\end{array} \)
\(\begin{array}{l}=2\sin \left( \alpha +\frac{2\pi }{3} \right)\cos \left( \frac{2\pi }{3} \right)+\sin \left( \alpha +\frac{2\pi }{3} \right)\end{array} \)
\(\begin{array}{l}=2\times \left( -\frac{1}{2} \right)\sin \left( \alpha +\frac{2\pi }{3} \right)+\sin \left( \alpha +\frac{2\pi }{3} \right)\end{array} \)
\(\begin{array}{l}=-\sin \left( \alpha +\frac{2\pi }{3} \right)+\sin \left( \alpha +\frac{2\pi }{3} \right)\end{array} \)
= 0
Example 4
\(\begin{array}{l}\text{If}\ a\sin \theta =b\sin \left( \theta +\frac{2\pi }{3} \right)=c\sin \left( \theta +\frac{4\pi }{3} \right),\ \text{then}\end{array} \)
prove that ab + bc + ca = 0.
Solution
\(\begin{array}{l}a\sin \theta =b\sin \left( \theta +\frac{2\pi }{3} \right)=c\sin \left( \theta +\frac{4\pi }{3} \right)=k\end{array} \)
\(\begin{array}{l}\sin \theta =\frac{k}{a}\end{array} \)
\(\begin{array}{l}\sin \left( \theta +\frac{2\pi }{3} \right)=\frac{k}{b}\end{array} \)
\(\begin{array}{l}\sin \left( \theta +\frac{4\pi }{3} \right)=\frac{k}{c}\end{array} \)
We know
\(\begin{array}{l}\sin \theta +\sin \left( \theta +\frac{2\pi }{3} \right)+\sin \left( \theta +\frac{4\pi }{3} \right)=0\end{array} \)
\(\begin{array}{l}\frac{k}{a}+\frac{k}{b}+\frac{k}{c}=0\end{array} \)
\(\begin{array}{l}\frac{k\left( bc+ac+ab \right)}{abc}=0\end{array} \)
\(\begin{array}{l}ab+bc+ca=0\end{array} \)
Summation of Series in Trigonometry
1.
\(\begin{array}{l}\sin \alpha +\sin \left( \alpha +\beta \right)+\sin \left( \alpha +2\beta \right)+……….+\sin \left( \alpha +\left( n-1 \right)\beta \right)=\frac{\sin \left[ \alpha +\frac{\left( n-1 \right)}{2}\beta \right]\sin \frac{n\beta }{2}}{\sin \frac{\beta }{2}}\end{array} \)
When the angles of sine are in AP, the sum of the sine series is given by the above formula.
However, if α = β in the above case,
Then
\(\begin{array}{l}\sin \alpha +\sin 2\alpha +\sin 3\alpha +……….+\sin \alpha =\frac{\sin \left( \frac{n+1}{2} \right)\alpha \sin \frac{n\alpha }{2}}{\sin \frac{\alpha }{2}}\end{array} \)
2. When cosine angles are in AP,
\(\begin{array}{l}cos\alpha +cos2\alpha +\cos \alpha +……….+\cos n\alpha =\frac{\cos \left( \frac{n+1}{2} \right)\alpha \sin \frac{n\alpha }{2}}{\sin \frac{\alpha }{2}}\end{array} \)
Remember
If A, B and C are angles of Δ,
\(\begin{array}{l}\sin \left( B+C \right)=\sin A\end{array} \)
\(\begin{array}{l}\cos \left( B+C \right)=-\cos A\end{array} \)
\(\begin{array}{l}\sin \left( \frac{B+C}{2} \right)=\cos \frac{A}{2}\end{array} \)
\(\begin{array}{l}\cos \left( \frac{B+C}{2} \right)=\sin \frac{A}{2}\end{array} \)
\(\begin{array}{l}\sin 2A+\sin 2B+\sin 2C=4\sin A\sin B\sin C\end{array} \)
\(\begin{array}{l}\cos 2A+\cos 2B+\cos 2C=1-4\cos A\cos B\cos C\end{array} \)
\(\begin{array}{l}\tan A+\tan B+\tan C=\tan A\tan B\tan C\end{array} \)
Trigonometric Equations
A solution of a trigonometric equation is the value of the unknown angle that satisfies the equation.
Following are general solutions of trigonometric equations in the standard form:
| Equation |
General Solution |
\(\begin{array}{l}\sin \theta =0 \end{array} \) |
\(\begin{array}{l}\theta =n\pi n\in z\end{array} \) |
\(\begin{array}{l}\cos \theta =0\end{array} \) |
\(\begin{array}{l}\theta =\left( 2n+1 \right)\frac{\pi }{2}n\in z\end{array} \) |
\(\begin{array}{l}\tan \theta =0\end{array} \) |
\(\begin{array}{l}\theta =n\pi ,n\in z\end{array} \) |
\(\begin{array}{l}\sin \theta =\sin \alpha \end{array} \) |
\(\begin{array}{l}\theta =n\pi +{{\left( -1 \right)}^{n}}\alpha ,n\in z\end{array} \) |
\(\begin{array}{l}\cos \theta =\cos \alpha \end{array} \) |
\(\begin{array}{l}\theta =2n\pi \pm \alpha ,n\in z\end{array} \) |
\(\begin{array}{l}\tan \theta =\tan \alpha\end{array} \) |
\(\begin{array}{l}\theta =n\pi +\alpha ,n\in z\end{array} \) |
\(\begin{array}{l}\left. \begin{matrix} {{\sin }^{2}}\theta ={{\sin }^{2}}\alpha \\ {{\cos }^{2}}\theta ={{\cos }^{2}}\alpha \\ {{\tan }^{2}}\theta ={{\tan }^{2}}\alpha \\ \end{matrix} \right\} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \theta =n\pi \pm \alpha ,n\in z\end{array} \)
Example 1
Solve
\(\begin{array}{l}4\sin x\sin 2x\sin 4x=\sin 3x\end{array} \)
Solution
\(\begin{array}{l}4\sin x\sin \left( 3x-x \right)\sin \left( 3x+x \right)=\sin 3x\end{array} \)
,
\(\begin{array}{l}4\sin x\left( {{\sin }^{2}}3x-{{\sin }^{2}}x \right)=\sin 3x\end{array} \)
,
\(\begin{array}{l}4\sin x.{{\sin }^{2}}3x-4{{\sin }^{3}}x=3\sin x-4{{\sin }^{3}}x\end{array} \)
,
\(\begin{array}{l}4\sin x{{\sin }^{2}}3x-3\sin x=0\end{array} \)
,
\(\begin{array}{l}\sin x\left( 4{{\sin }^{2}}3x-3 \right)=0\end{array} \)
,
\(\begin{array}{l}\sin x=0\;\; and \;\;{{\sin }^{2}}3x=\frac{3}{4}\end{array} \)
,
\(\begin{array}{l}n\in z\end{array} \)
,
\(\begin{array}{l}{{\sin }^{2}}3x=\frac{3}{4}\end{array} \)
,
\(\begin{array}{l}{{\sin }^{2}}3x={{\left( \frac{\sqrt{3}}{4} \right)}^{2}}={{\sin }^{2}}\frac{\pi }{3}\end{array} \)
,
\(\begin{array}{l}3x=m\pi \pm \frac{\pi }{3}m\in z\end{array} \)
,
\(\begin{array}{l}x=\frac{m\pi }{3}\pm \frac{\pi }{9}\end{array} \)
Example 2
Solve
\(\begin{array}{l}\sin 3\theta +\cos 2\theta =0\end{array} \)
Solution
\(\begin{array}{l}\cos 2\theta =-\sin 3\theta\end{array} \)
.
Taking +ve sign
\(\begin{array}{l}\theta =2n\pi +\frac{\pi }{2}+3\theta\end{array} \)
,
\(\begin{array}{l}-\theta =2n\pi +\frac{\pi }{2}\end{array} \)
,
\(\begin{array}{l}\theta =-2n\pi -\frac{\pi }{2}\end{array} \)
or
Taking -ve sign
\(\begin{array}{l}\theta =2n\pi +\frac{\pi }{2}-3\theta; n\in z\end{array} \)
,
\(\begin{array}{l}4\theta =2n\pi +\frac{\pi }{2}\end{array} \)
,
\(\begin{array}{l}\theta =\frac{n\pi }{2}+\frac{\pi }{8}\end{array} \)
Example 3
Solve
\(\begin{array}{l}\sqrt{3}\sec 2\theta =2\end{array} \)
Solution
\(\begin{array}{l}\frac{\sqrt{3}}{\cos 2\theta }=2\end{array} \)
,
\(\begin{array}{l}\cos 2\theta =\frac{\sqrt{3}}{2}=\cos \frac{\pi }{6}\end{array} \)
,
\(\begin{array}{l}2\theta =2n\pi \pm \frac{\pi }{6}n\in z\end{array} \)
,
\(\begin{array}{l}\theta =n\pi \pm \frac{\pi }{12}n\in z\end{array} \)
Properties and Solutions of Triangle
Solutions of Triangle
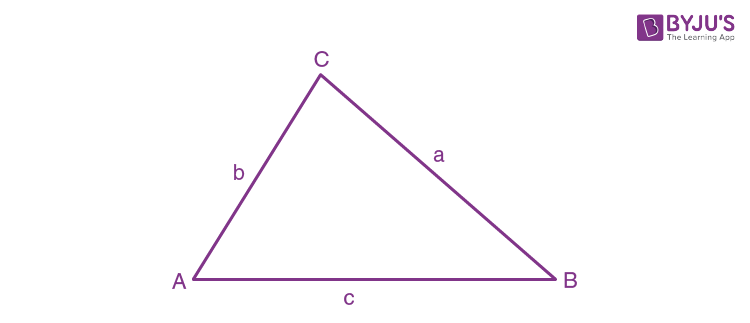
Here A, B and C are the angles, and a, b and c are the lengths of sides of the triangle ABC.
Sine Rule
The sine rule relates the length of the sides of a triangle to the sines of its angles.
\(\begin{array}{l}\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R\end{array} \)
Where 2R is the diameter of the triangle’s circumcircle.
Cosine Rule
\(\begin{array}{l}\cos A=\frac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}\end{array} \)
and
\(\begin{array}{l}\cos B=\frac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac}\end{array} \)
and
\(\begin{array}{l}\cos C=\frac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab}\end{array} \)
Area of Δ
\(\begin{array}{l} =\frac{1}{2}bc\sin A\end{array} \)
\(\begin{array}{l}=\frac{1}{2}ca\sin B\end{array} \)
\(\begin{array}{l}=\frac{1}{2}ab\sin C\end{array} \)
\(\begin{array}{l}=\sqrt{S\left( S-a \right)\left( S-b \right)\left( S-c \right)}\end{array} \)
\(\begin{array}{l}=\frac{1}{2}\times base\times height\end{array} \)
Projection Formula
a=b cos c+c cos B
b=c cos A+a cos C
c=a cos B+b cos A
Napier’s Analogy
This is also called the Law of Tangents.
\(\begin{array}{l}\tan \left( \frac{B-C}{3} \right)=\left( \frac{b-c}{b+c} \right)\cot \frac{A}{2}\end{array} \)
,
\(\begin{array}{l}\tan \left( \frac{C-A}{2} \right)=\left( \frac{c-a}{c+a} \right)\cot \frac{B}{2}\end{array} \)
,
\(\begin{array}{l}\tan \left( \frac{A-B}{2} \right)=\left( \frac{a-b}{a+b} \right)\cot \frac{C}{2}\end{array} \)
Example
In a triangle ABC,
\(\begin{array}{l}\frac{a+b}{13}=\frac{a+c}{12}=\frac{b+c}{11}\end{array} \)
Then prove that
\(\begin{array}{l}\frac{\cos A}{7}=\frac{\cos B}{19}=\frac{\cos C}{25}\end{array} \)
Solution
\(\begin{array}{l}\frac{b+c}{11}=\frac{c+a}{12}=\frac{a+b}{13}=k\end{array} \)
,
\(\begin{array}{l}b+c=11k,c+a=12k,a+b=13k\end{array} \)
,
\(\begin{array}{l}2\left( a+b+c \right)=36k\end{array} \)
,
\(\begin{array}{l}a+b+c=18k\end{array} \)
b+c=11k
a=7k
Similarly, b=6k
c=5k
\(\begin{array}{l}\cos A=\frac{{{b}^{2}}{{c}^{2}}-{{a}^{2}}}{2bc}=\frac{36{{k}^{2}}+25{{k}^{2}}-49{{k}^{2}}}{60{{k}_{2}}}=\frac{1}{5}\end{array} \)
Similarly,
\(\begin{array}{l}\cos B=\frac{19}{35}\; and \; \cos C=\frac{5}{7}\end{array} \)
,
\(\begin{array}{l}\cos A:\cos B:\cos C=\frac{1}{5}:\frac{19}{35}:\frac{8}{7}\end{array} \)
=7:19:25
Circum Circle of a Triangle
The circle passing through the vertices of a triangle is called the circum circle of a triangle.
The radius is the circum radius.
\(\begin{array}{l}R=\frac{a}{2{sinA}}=\frac{b}{2\sin B}=\frac{c}{2\sin C}\end{array} \)
Also,
\(\begin{array}{l}R=\frac{abc}{4\Delta }\end{array} \)
; \(\begin{array}{l}\Delta is \;the\; area\; of\; \Delta ABC\end{array} \)
Inradius of a Triangle
\(\begin{array}{l}r=\frac{\Delta }{s} \;where \;\Delta =\;area \;of \;\Delta\end{array} \)
,
\(\begin{array}{l}s=\frac{a+b+c}{2}\end{array} \)
,
\(\begin{array}{l}r=\left( s-a \right)\tan \frac{A}{2}=\left( s-b \right)\tan \frac{B}{2}=\left( s-c \right)\tan \frac{C}{2}\end{array} \)
,
\(\begin{array}{l}r=4R\sin \frac{A}{2}\sin \frac{B}{2}\sin \frac{C}{2}\end{array} \)
Example
In a triangle ABC, angle C = 60 degrees.
Then prove that
\(\begin{array}{l}\frac{1}{a+c}+\frac{1}{b+c}=\frac{3}{a+b+c}\end{array} \)
Solution
\(\begin{array}{l}\cos c=\frac{1}{2}=\frac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ba}\end{array} \)
,
\(\begin{array}{l}ab={{a}^{2}}+{{b}^{2}}-{{c}^{2}}\rightarrow{{}}\left( i \right)\end{array} \)
,
\(\begin{array}{l}\frac{1}{a+c}+\frac{1}{b+c}=\frac{3}{a+b+c}\end{array} \)
,
\(\begin{array}{l}\frac{a+b+c+c}{\left( a+c \right)\left( b+c \right)}=\frac{3}{a+b+c}\end{array} \)
,
\(\begin{array}{l}\left( a+b+2c \right)\left( a+b+c \right)=3\left( a+c \right)\left( b+c \right)\end{array} \)
,
\(\begin{array}{l}{{a}^{2}}+{{b}^{2}}+2ab+2{{c}^{2}}+3ac+3bc=3ab+3ac+3bc+3{{c}^{2}}\end{array} \)
,
\(\begin{array}{l}{{a}^{2}}{{b}^{2}}-ab={{c}^{2}}\rightarrow{{}}\left( ii \right)\end{array} \)
From (i) and (ii), we can say
\(\begin{array}{l}\frac{1}{a+c}+\frac{1}{b+c}=\frac{3}{a+b+c}\end{array} \)
Trigonometry Videos
Trigonometry Phase 1 Important Questions
Trigonometry Phase 2 Important Questions
Solving Trigonometric Functions
Trigonometric Functions Session 1
Trigonometric Functions Session 2
Trigonometric Ratios of Compound Angles
Trigonometric Equations General Solution
Frequently Asked Questions
Q1
What is trigonometry?
Trigonometry is a branch of mathematics that deals with the relationship between the sides of a triangle (right triangle) with its angles.
Q2
Name the six basic trigonometric functions.
The basic trigonometric functions are sin, cos, tan, sec, cosec and cot.
Q3
Give the Pythagorean trigonometric identities.
sin2a + cos2a = 1
1 + tan2a = sec2a
1 + cot2 a = cosec2a
Q4
Give an application of trigonometry.
The height of an object or the distance between two distinct objects can be calculated using trigonometric ratios.






















Comments