DefinitionFormulaProofPropertiesSolved Examples
Download Complete Chapter Notes of Mathematical Tools
Download Now
Vector Triple Product is a branch in vector algebra where we deal with the cross product of three vectors. The value of the vector triple product can be found by the cross product of a vector with the cross product of the other two vectors. It gives a vector as a result. When we simplify the vector triple product, it gives us an identity name as BAC-CAB identity.
Vector Triple Product Definition
Vector triple product of three vectors
\(\begin{array}{l}\vec a, \vec b, \vec c\ \text{is defined as the cross product of vector}\ \vec{a}\end{array} \)
\(\begin{array}{l}\text{with the cross product of vectors}\ \vec b\ and\ \vec c,\end{array} \)
\(\begin{array}{l}i.e.,\ \vec a \times (\vec b \times \vec c)\end{array} \)
Here,
\(\begin{array}{l}\vec a \times (\vec b \times \vec c)\ \text{is coplanar with the vectors}\ \vec{b}\ \text{and}\ \vec{c}\ \text{and perpendicular to}\ \vec{a}.\end{array} \)
Hence we can write
\(\begin{array}{l}\vec a \times (\vec b \times \vec c)\ \text{as linear combination of vectors}\ \vec{b}\ \text{and}\ \vec{c}.\end{array} \)
That is,
\(\begin{array}{l}\vec a \times (\vec b \times \vec c) = x \vec b + y \vec c\end{array} \)
Vector Triple Product Formula
\(\begin{array}{l}\vec a \times (\vec b \times \vec c) = (\vec a . \vec c) \vec b\ – (\vec a . \vec b) \vec c\end{array} \)
and
\(\begin{array}{l}(\vec a \times \vec b) \times \vec c = (\vec a . \vec c) \vec b\ – (\vec b . \vec c) \vec a\end{array} \)
In general,
\(\begin{array}{l}\vec a \times (\vec b \times \vec c) \neq (\vec a \times \vec b) \times \vec c\end{array} \)
Vector Triple Product Proof
We can write
\(\begin{array}{l}(\vec a \times \vec b) \times \vec c\ \text{as a linear combination of vectors}\ \vec{a}\ \text{and}\ \vec{b}.\end{array} \)
So,
\(\begin{array}{l}(\vec a \times \vec b) \times \vec c = x \vec a + y \vec b\end{array} \)
\(\begin{array}{l}\Rightarrow \vec c . (\vec a \times \vec b) \times \vec c = \vec c . (x \vec a + y \vec b)\end{array} \)
\(\begin{array}{l}= x . (\vec c . \vec a) + y (\vec c . \vec b)\end{array} \)
\(\begin{array}{l}\Rightarrow 0 = x . (\vec a . \vec c) + y (\vec b . \vec c)\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{x}{\vec b . \vec c} = \frac{-y}{\vec a . \vec c} = \lambda\end{array} \)
\(\begin{array}{l}\text{Substituting value of x and y in}\ (\vec a \times \vec b) \times \vec c = x \vec a + y \vec b,\end{array} \)
we have;
\(\begin{array}{l}(\vec a \times \vec b) \times \vec c = (\lambda \vec b . \vec c) \vec a + (-\lambda \vec a . \vec c) \vec b\end{array} \)
\(\begin{array}{l}=(\lambda \vec b . \vec c) \vec a – (\lambda \vec a . \vec c) \vec b\end{array} \)
\(\begin{array}{l}\text{It is valid for every value of}\ \vec a, \vec b, \vec c\ \text{because it is an identity}.\end{array} \)
Put
\(\begin{array}{l} \vec a = \hat i , \vec b = \hat j\ and\ \vec c = \hat i\end{array} \)
\(\begin{array}{l}\Rightarrow (\hat i \times \hat j) \times \hat i = (\lambda \hat j . \hat i) \hat i – (\lambda \hat i . \hat i) \hat j\end{array} \)
\(\begin{array}{l}\Rightarrow \hat j = – \lambda \hat j \end{array} \)
\(\begin{array}{l}\Rightarrow \lambda = -1 \end{array} \)
Hence,
\(\begin{array}{l}(\vec a \times \vec b) \times \vec c = (\vec a . \vec c)\vec b – (\vec b . \vec c)\vec a \end{array} \)
Properties
- A vector triple product is a vector quantity.
\(\begin{array}{l}\text{Unit vector coplanar with}\ \vec a\ \text{and}\ \vec b \end{array} \)
\(\begin{array}{l}\text{and perpendicular to}\ \vec c\ \text{is}\ \pm \frac{(\vec a \times \vec b)\times \vec c}{|(\vec a \times \vec b)\times \vec c|}.\end{array} \)
\(\begin{array}{l}\vec a \times (\vec b \times \vec c) \neq (\vec a \times \vec b) \times \vec c\end{array} \)
.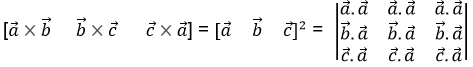
Note that,
\(\begin{array}{l}\text{if}\ \vec a, \vec b, \vec c\ \text{are non-coplanar vector then}\end{array} \)
\(\begin{array}{l} \vec a \times \vec b, \vec b \times \vec c\ and\ \vec c \times \vec a\ \text{are also non-coplanar.}\end{array} \)
Some other useful results:

Solved Examples
Example 1:
\(\begin{array}{l}\text{Find the value of}\ \hat i \times (\hat j \times \hat k) + \hat j \times (\hat k \times \hat i).\end{array} \)
Solution:
\(\begin{array}{l} \hat i \times (\hat j \times \hat k) + \hat j \times (\hat k \times \hat i) = \hat i \times \hat i + \hat j \times -\hat j = 1-1= 0 \end{array} \)
Example 2:
\(\begin{array}{l}\text{If}\ \vec a, \vec b, \vec c\ \text{are three vectors such that}\end{array} \)
\(\begin{array}{l}| \vec a| = 1,\ | \vec b|=2,\ | \vec c|=1,\ \text{and}\ \vec a \times (\vec a \times \vec b) + \vec c = 0,\end{array} \)
\(\begin{array}{l}\text{then find the acute angle between}\ \vec a\ \text{and}\ \vec b.\end{array} \)
Solution:
\(\begin{array}{l}\text{Let A be the angle between}\ \vec a\ \text{and}\ \vec b.\end{array} \)
Then,
\(\begin{array}{l} \vec a . \vec b = |\vec a||\vec b|cos\ A\end{array} \)
= 1.2. cos A
= 2 cos A
But
\(\begin{array}{l} \vec a \times (\vec a \times \vec b) + \vec c = 0\end{array} \)
\(\begin{array}{l}\Rightarrow (\vec a . \vec b)\vec a – (\vec a . \vec a)\vec b + \vec c = 0\end{array} \)
\(\begin{array}{l}\Rightarrow 2\ cos\ A \vec a – \vec b + \vec c = 0\end{array} \)
\(\begin{array}{l}\Rightarrow 2\ cos\ A \vec a – \vec b =- \vec c\end{array} \)
Squaring both sides, we have;
\(\begin{array}{l}\Rightarrow [2\ cos\ A \vec a – \vec b]^2 = [- \vec c]^2\end{array} \)
\(\begin{array}{l}\Rightarrow 4 cos^2 A |\vec a|^2 – 4 cos A \vec a . \vec b + |\vec b|^2 = |\vec c|^2 \end{array} \)
⇒ 4 cos2 A – 4 cos A . 2 cos A + 4 = 1
⇒ 4 cos2 A – 8 cos2 A + 4 = 1
\(\begin{array}{l}\Rightarrow 4 (1 – cos^2 A) = 1 \end{array} \)
⇒ 4 sin2 A = 1
or sin A = 1/2
or A = π/6
[neglected -ve value]
Example 3:
\(\begin{array}{l}\text{If}\ \vec a, \vec b, \vec c\ \text{are coplanar, then prove that}\end{array} \)
\(\begin{array}{l} \vec a \times \vec b,\ \vec b \times \vec c,\ \vec c \times \vec a\ \text{are also coplanar.}\end{array} \)
Solution:
\(\begin{array}{l}\text{If}\ \vec a, \vec b, \vec c\ \text{are coplanar then}\end{array} \)
\(\begin{array}{l}[\vec a\;\; \vec b\;\; \vec c]\end{array} \)
\(\begin{array}{l}\Rightarrow [\vec a\;\; \vec b\;\; \vec c]^2 = 0\end{array} \)
\(\begin{array}{l}\Rightarrow [\vec a \times \vec b\;\; \vec b \times \vec c\;\; \vec c \times \vec a] = 0\end{array} \)
\(\begin{array}{l}\text{So we can say that}\ \vec a \times \vec b, \vec b \times \vec c, \vec c \times \vec a\ \text{are coplanar}.\end{array} \)
Example 4:
\(\begin{array}{l}\text{Let}\ \vec c = 2 \hat i + \hat j – 2 \hat k\ \text{and}\ \vec b = \hat i + \hat j \end{array} \)
\(\begin{array}{l}\text{and if vector}\ \vec a\ \text{is such that}\ \vec{c}.\vec{a} = |\vec a|,\ |\vec a – \vec c| = 2\sqrt{2}\end{array} \)
\(\begin{array}{l}\text{and angle between}\ (\vec c \times \vec b)\ \text{and}\ \vec{a}\ \text{is}\ \frac{\pi}{6},\end{array} \)
\(\begin{array}{l}\text{then find the value of}\ |(\vec c \times \vec b) \times \vec a|.\end{array} \)
Solution:
\(\begin{array}{l} \vec c = 2 \hat i + \hat j – 2 \hat k\ and\ \vec b = \hat i + \hat j \end{array} \)
so,
\(\begin{array}{l} |\vec c| = 3\ \text{and}\ |\vec b| = \sqrt{2}\end{array} \)
\(\begin{array}{l} |\vec a – \vec c| = 2\sqrt{2}\ (\text{Given})\end{array} \)
Squaring both sides, we have;
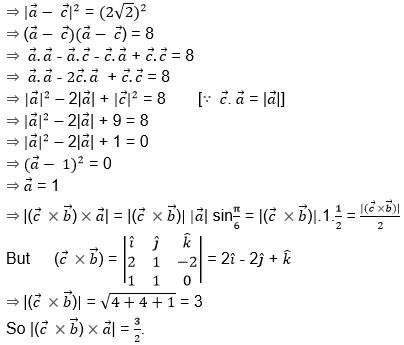
Example 5: If
\(\begin{array}{l}\mathbf{a}\times \mathbf{b}=\mathbf{c},\,\,\mathbf{b}\times \mathbf{c}=\mathbf{a}\end{array} \)
and a, b, c be moduli of the vectors a, b, c respectively, then find the values of a and b.
Solution:
a = b × c and a × b = c
∴ a is perpendicular to both b and c, and c is perpendicular to both a and b.
Therefore, a, b, and c are mutually perpendicular.
Now, a = b × c = b × (a × b) = (b . b) a − (b . a) b or
\(\begin{array}{l}\mathbf{a}={{b}^{2}}\mathbf{a}-(\mathbf{b}\,.\,\mathbf{a})\mathbf{b}={{b}^{2}}\mathbf{a}, \left\{ \text because \,\mathbf{a}\,\bot \,\mathbf{b} \right\} \\\Rightarrow 1={{b}^{2}}, \\\therefore \,\mathbf{c}=\mathbf{a}\times \mathbf{b}=ab\sin 90{}^\circ \,\mathbf{\hat{n}}\end{array} \)
Take the moduli of both sides, then c = ab, but b = 1 ⇒ c = a.
Example 6: Given the following simultaneous equations for vectors x and y.
x + y = a …..(i)
x × y = b …..(ii)
x . a = 1 …..(iii)
Then find the values of x and y.
Solution:
Multiplying (i) by scalar “a”, we get;
a . x + a . y = a2
∴ a . y = a2 − 1 ..(iv),
{By (iii)} Again a × (x × y) = a × b or (a . y) x − (a . x) y = a × b
(a2 − 1) x − y = a × b ..(v),
Adding and subtracting (i) and (v), we get;
x = [a + (a × b)] / [a2] and y = a − x
Vector Triple Point
Frequently Asked Questions
Q1
What do you mean by vector triple product?
Let a, b, and c be three vectors. The vector product of a, b, and c is the cross product of vector a with the cross product of vector b and vector c.
Q2
Give the vector triple product formula.
If a, b, c are three vectors, then
a × (b × c) = (a.c)b – (a.b)c.
(a × b) × c = (a.c)b – (b.c)a.
Q3
Is the vector triple product associative?
No, the vector triple product is not associative.
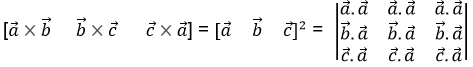

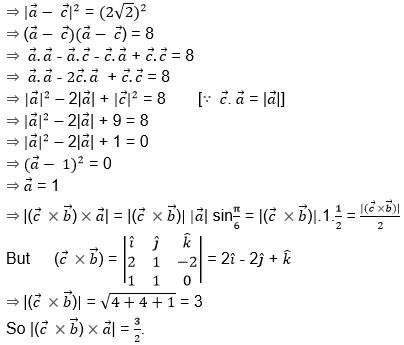


Comments