Binomial Theorem – As the power increases, the expansion becomes lengthy and tedious to calculate. A binomial expression that has been raised to a very large power can be easily calculated with the help of the Binomial Theorem. On this page, you will learn the definition and statement of binomial theorem, binomial expansion formulas, properties of binomial theorem, how to find the binomial coefficients, terms in the binomial expansion, applications, etc.
Download Complete Chapter Notes of Binomial Theorem
Download Now
| Table of Contents: |
To learn all the details about the binomial theorem, like its definition, formulas, properties, applications, etc., download the binomial theorem PDF lesson below.
Download this lesson as PDF:-Binomial Theorem PDF
Binomial Theorem Statement
The binomial theorem is the method of expanding an expression that has been raised to any finite power. A binomial theorem is a powerful tool of expansion which has applications in Algebra, probability, etc.
Binomial Expression: A binomial expression is an algebraic expression that contains two dissimilar terms. Eg.., a + b, a3 + b3, etc.
Binomial Expansion
Important points to remember
- The total number of terms in the expansion of (x+y)n is (n+1)
- The sum of exponents of x and y is always n.
- nC0, nC1, nC2, … .., nCn are called binomial coefficients and also represented by C0, C1, C2, ….., Cn
- The binomial coefficients, which are equidistant from the beginning and from the ending, are equal, i.e., nC0 = nCn, nC1 = nCn-1 , nC2 = nCn-2 ,….. etc.
Binomial Expansion Formula: Let n ∈ N,x,y,∈ R then
(x + y)n = nΣr=0 nCr xn – r · yr where,

Illustration 1: Expand (x/3 + 2/y)4
Sol:

Illustration 2: (√2 + 1)5 + (√2 − 1)5
Sol:
We have
(x + y)5 + (x – y)5 = 2[5C0 x5 + 5C2 x3 y2 + 5C4 xy4]
= 2(x5 + 10 x3 y2 + 5xy4)
Now (√2 + 1)5 + (√2 − 1)5 = 2[(√2)5 + 10(√2)3(1)2 + 5(√2)(1)4]
=58√2
Binomial Expansion Formulas
To find binomial coefficients, we can also use Pascal’s Triangle.
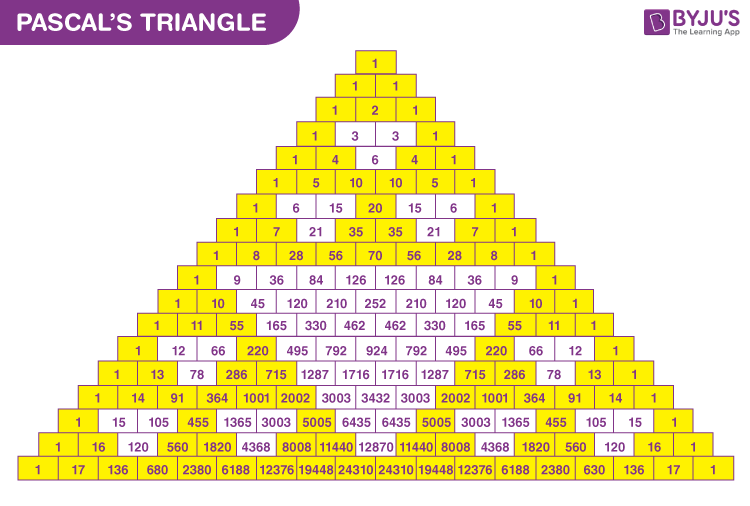
Finding binomial coefficients with Pascal’s Triangle
Some other useful expansions:
- (x + y)n + (x−y)n = 2[C0 xn + C2 xn-1 y2 + C4 xn-4 y4 + …]
- (x + y)n – (x−y)n = 2[C1 xn-1 y + C3 xn-3 y3 + C5 xn-5 y5 + …]
- (1 + x)n = nΣr-0 nCr . xr = [C0 + C1 x + C2 x2 + … Cn xn]
- (1+x)n + (1 − x)n = 2[C0 + C2 x2+C4 x4 + …]
- (1+x)n − (1−x)n = 2[C1 x + C3 x3 + C5 x5 + …]
- The number of terms in the expansion of (x + a)n + (x−a)n is (n+2)/2 if “n” is even or (n+1)/2 if “n” is odd.
- The number of terms in the expansion of (x + a)n − (x−a)n is (n/2) if “n” is even or (n+1)/2 if “n” is odd.
Number of Terms and R-F Factor Relation

Properties of Binomial Coefficients
Binomial coefficients refer to the integers, which are coefficients in the binomial theorem. Some of the most important properties of binomial coefficients are:
- C0 + C1 + C2 + … + Cn = 2n
- C0 + C2 + C4 + … = C1 + C3 + C5 + … = 2n-1
- C0 – C1 + C2 – C3 + … +(−1)n . nCn = 0
- nC1 + 2.nC2 + 3.nC3 + … + n.nCn = n.2n-1
- C1 − 2C2 + 3C3 − 4C4 + … +(−1)n-1 Cn = 0 for n > 1
- C02 + C12 + C22 + …Cn2 = [(2n)!/ (n!)2]
Illustration: If (1 + x)15 = a0 + a1x + . . . . . + a15 x15 then, find the value of 
Sol:
![]()
= C1/C0 + 2 C2/C1+ 3C3/C2 + . . . . + 15 C15/C14
= 15 + 14 + 13 + . . . . . + 1 = [15(15+1)]/2 = 120
Properties of Binomial Coefficients Video Lesson

Terms in the Binomial Expansion
In binomial expansion, it is often asked to find the middle term or the general term. The different terms in the binomial expansion that are covered here include
- General Term
- Middle Term
- Independent Term
- Determining a Particular Term
- Numerically Greatest Term
- Ratio of Consecutive Terms/Coefficients
General Term in Binomial Expansion:
We have (x + y)n = nC0 xn + nC1 xn-1 . y + nC2 xn-2 . y2 + … + nCn yn
General Term = Tr+1 = nCr xn-r . yr
- General Term in (1 + x)n is nCr xr
- In the binomial expansion of (x + y)n, the rth term from the end is (n – r + 2)th.
Illustration: Find the number of terms in (1 + 2x +x2)50
Sol:
(1 + 2x + x2)50 = [(1 + x)2]50 = (1 + x)100
The number of terms = (100 + 1) = 101
Illustration: Find the fourth term from the end in the expansion of (2x – 1/x2)10
Sol:
Required term =T10 – 4 + 2 = T8 = 10C7 (2x)3 (−1/x2)7 = −960x-11
Middle Term(s) in the Expansion of (x+y) n.n
- If n is even, then (n/2 + 1) Term is the middle term.
- If n is odd then, [(n+1)/2]th and [(n+3)/2)th terms are the middle terms.
Illustration: Find the middle term of (1 −3x + 3x2 – x3)2n
Sol:
(1 − 3x + 3x2 – x3)2n = [(1 − x)3]2n = (1 − x)6n
Middle Term = [(6n/2) + 1] term = 6nC3n (−x)3n
Determining a Particular Term:
- In the expansion of (axp + b/xq)n the coefficient of xm is the coefficient of Tr+1 where r = [(np−m)/(p+q)]
- In the expansion of (x + a)n, Tr+1/Tr = (n – r + 1)/r . a/x
General and Middle Terms of Binomial Expansion

Independent Term
The term Independent of in the expansion of [axp + (b/xq)]n is
Tr+1 = nCr an-r br, where r = (np/p+q) (integer)
Illustration: Find the independent term of x in (x+1/x)6
Sol:
r = [6(1)/1+1] = 3
The independent term is 6C3 = 20
Illustration: Find the independent term in the expansion of:

Sol:

(x1/3 + 1 – 1 – 1/√x)10 = (x1/3 – 1/√x)10
r = [10(1/3)]/[1/3+1/2] = 4
∴ T5 = 10C4 = 210
Numerically Greatest Term in the Expansion of (1+x)n:
- If [(n+1)|x|]/[|x|+1] = P, is a positive integer, then the Pth term and (P+1)th terms are numerically the greatest terms in the expansion of (1+x)n
- If[(n+1)|x|]/[|x|+1] = P + F, where P is a positive integer, and 0 < F < 1, then (P+1)th term is numerically the greatest term in the expansion of (1+x)n.
Illustration: Find the numerically greatest term in (1-3x)10 when x = (1/2)
Sol:
[(n + 1)|α|] / [|α| + 1] = (11 × 3/2)/(3/2+1) = 33/5 = 6.6
Therefore, T7 is the numerically greatest term.
T6 + 1 = 10C6 . (−3x)6 = 10C6 . (3/2)6
Ratio of Consecutive Terms/Coefficients:
The coefficients of xr and xr + 1 are nCr – 1 and nCr, respectively.
(nCr / nCr – 1) = (n – r + 1) / r
Illustration: If the coefficients of three consecutive terms in the expansion of (1+x)n are in the ratio 1:7:42, then find the value of n.
Sol:
Let (r – 1)th, (r)th and (r + 1)th be the three consecutive terms.
Then, the given ratio is 1:7:42
Now (nCr-2 / nCr – 1) = (1/7)
(nCr-2 / nCr – 1) = (1/7) ⇒ [(r – 1)/(n − r+2)] = (1/7) ⇒ n−8r+9=0 → (1)
And,
(nCr-1 / nCr) = (7/42) ⇒ [(r)/(n – r +1)] =(1/6) ⇒ n−7r +1=0 → (2)
From (1) & (2), n = 55
Applications of Binomial Theorem
The binomial theorem has a wide range of applications in Mathematics, like finding the remainder, finding the digits of a number, etc. The most common binomial theorem applications are as follows:
Finding Remainder Using Binomial Theorem
Illustration: Find the remainder when 7103 is divided by 25.
Sol:
(7103 / 25) = [7(49)51 / 25)] = [7(50 − 1)51 / 25]
= [7(25K − 1) / 25] = [(175K – 25 + 25−7) / 25]
= [(25(7K − 1) + 18) / 25]
∴ The remainder = 18
Illustration: If the fractional part of the number (2403 / 15) is (K/15), then find K.
Sol:
(2403 / 15) = [23 (24)100 / 15]
= 8/15 (15 + 1)100 = 8/ 15 (15λ + 1) = 8λ + 8/15
∵ 8λ is an integer, fractional part = 8/15
So, K = 8.
Finding Digits of a Number
Illustration: Find the last two digits of the number (13)10
Sol:
(13)10 = (169)5 = (170 − 1)5
= 5C0 (170)5 − 5C1 (170)4 + 5C2 (170)3 − 5C3 (170)2 + 5C4 (170) − 5C5
= 5C0 (170)5 − 5C1 (170)4 + 5C2 (170)3 − 5C3 (170)2 + 5(170) − 1
A multiple of 100 + 5(170) – 1 = 100K + 849
∴ The last two digits are 49.
Relation between Two Numbers
Illustration: Find the larger of 9950 + 10050 and 10150
Sol:
10150 = (100 + 1)50 = 10050 + 50 . 10049 + 25 . 49 . 10048 + …
⇒ 9950 = (100 − 1)50 = 10050 – 50 . 10049 + 25 . 49 . 10048 − ….
⇒ 10150 – 9950 = 2[50 . 10049 + 25(49) (16) 10047 + …]
= 10050 + 50 . 49 . 16 . 10047 + … >10050
∴ 10150 – 9950 > 10050
⇒ 10150 > 10050 + 9950
Divisibility Test
Illustration: Show that 119 + 911 is divisible by 10.
Sol:
119 + 911 = (10 + 1)9 + (10 − 1)11
= (9C0 . 109 + 9C1 . 108 + … 9C9) + (11C0 . 1011 − 11C1 . 1010 + … −11C11)
= 9C0 . 109 + 9C1 . 108 + … + 9C8 . 10 + 1 + 1011 − 11C1 . 1010 + … + 11C10 . 10−1
= 10[9C0 . 108 + 9C1 . 107 + … + 9C8 + 11C0 . 1010 − 11C1 . 109 + … + 11C10]
= 10K, which is divisible by 10.
Formulae:
- The number of terms in the expansion of (x1 + x2 + … xr)n is (n + r − 1)Cr – 1
- The sum of the coefficients of (ax + by)n is (a + b)n
If f(x) = (a0 + a1x + a2x2 + …. + amxm)n then
- (a) Sum of coefficients = f(1)
- (b) Sum of coefficients of even powers of x is: [f(1) + f(−1)] / 2
- (c) Sum of coefficients of odd powers of x is [f(1) − f(−1)] / 2
Binomial Theorem for Any Index
Let n be a rational number and x be a real number, such that | x | < 1. Then,
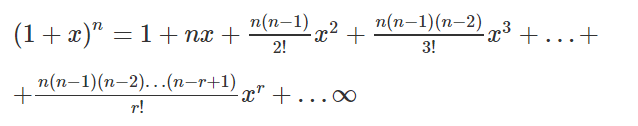
Proof:
Let f(x) = (1 + x)n = a0 + a1 x + a2 x2 + … +ar xr + … (1)
f(0) = (1 + 0)n = 1
Differentiating (1) w.r.t. x on both sides, we get
n(1 + x)n – 1
= a1 + 2a2 x + 3a3 x3 + 4a4 x3 + … + rar xr – 1 + … (2)
Put x = 0, we get n = a1
Differentiating (2) w.r.t. x on both sides, we get
n(n − 1)(1 + x)n – 2
= 2a2 + 6a3 x + 12a4 x2 + … + r(r−1) ar xr – 2 + … (3)
Put x = 0, we get a2 = [n(n−1)] / 2!
Differentiating (3), w.r.t. x on both sides, we get
n(n − 1)(n − 2)(1 + x)n – 3 = 6a3 + 24a4 x + … + r(r − 1)(r − 2) ar xr – 3 + …
Put x = 0, we get a3 = [n(n−1)(n−2)] / 3!
Similarly, we get a4 = [n(n−1)(n−2)(n−3)] / r! and so on
∴ ar = [n(n−1)(n−2)…(n−r+1)] / r!
Putting the values of a0, a1, a2, a3, …, ar obtained in (1), we get
(1 + x)n = 1 + nx + [{n(n−1)} / 2!] x2 + [{n(n − 1)(n − 2)} / 2!] x3 + … + [{n(n − 1)(n − 2) … (n – r + 1)}/ r!] xr + …
Binomial Theorem for Rational Index
The number of rational terms in the expression of (a1/l + b1/k )n is [n / LCM of {l,k}] when none of and is a factor of and when at least one of and is a factor of is [n / LCM of {l,k}] + 1 where [.] is the greatest integer function.
Illustration: Find the number of irrational terms in (8√5 + 6√2)100.
Sol:
Tr + 1 = 100Cr (8√5)100 – r . (6√2)r = 100Cr . 5[(100 – r)/8] .2r/6.
∴ r = 12,36,60,84
The number of rational terms = 4
The number of irrational terms = 101 – 4 = 97
Binomial Theorem for Negative Index
1. If the rational number and -1 < x <1, then,
- (1 − x)-1 = 1 + x + x2 + x3 + … + xr + … ∞
- (1 + x)-1 = 1 – x + x2 – x3 + … (−1)r xr+ … ∞
- (1 − x)-2 = 1 + 2x + 3x2 − 4x3 + … + (r + 1)xr + … ∞
- (1 + x)-2 = 1 − 2x + 3x2 − 4x3 + … + (−1)r (r + 1)xr + … ∞
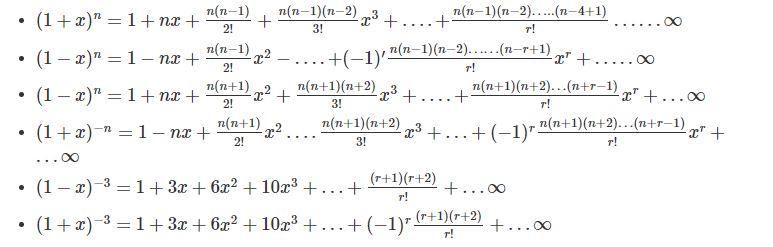
2. Number of terms in (1 + x)n is
- ‘n+1 when positive integer.
- Infinite when is not a positive integer & | x | < 1
3. First negative term in (1 + x)p/q when 0 < x < 1, p, q are positive integers & ‘p’ is not a multiple of ‘q’ is T[p/q] + 3
Multinomial Theorem
Using the binomial theorem, we have
(x + a)n
=n∑r = 0nCr xn – r ar, n∈N
= n∑r = 0 [n! / (n − r)!r!] xn – rar
= n∑r + s =n [n! / r!s!] xs ar, where s = n – r.
This result can be generalised in the following form:
(x1 + x2 + … +xk)n
= ∑r1 + r2 + …. + rk = n [n! / r1!r2!…rk!] x1r1 x2r2 …xkrk
The general term in the above expansion is
[(n!) / (r1! r2! r3! … rk!)] x1r1 x2r2 x3r3… xkrk
The number of terms in the above expansion is equal to the number of non-negative integral solutions of the equation.
r1+r2 + … + rk = n, because each solution of this equation gives a term in the above expansion. The number of such solutions is n + k – 1Ck −1.
PARTICULAR CASES
Case-1:

The above expansion has n+3-1C3-1 = n + 2C2 terms.
Case-2:

There are n + 4 – 1C4 – 1 = n + 3C3 terms in the above expansion.
REMARK: The greatest coefficient in the expansion of (x1 + x2 + … + xm)n is [(n!) / (q!)m – r{(q+1)!}r], where q and r are the quotient and remainder, respectively, when n is divided by m.
Multinomial Expansions
Consider the expansion of (x + y + z)10. In the expansion, each term has different powers of x, y, and z, and the sum of these powers is always 10.
One of the terms is λx2y3z5. Now, the coefficient of this term is equal to the number of ways 2x′s, 3y′s, and 5z′s are arranged, i.e., 10! (2! 3! 5!). Thus,
(x+y+z)10 = ∑(10!) / (P1! P2! P3!) xP1 yP2 zP3
Where P1 + P2 + P3 = 10 and 0 ≤ P1, P2, P3 ≥ 10
In general,
(x1 + x2 + … xr)n = ∑ (n!) / (P1! P2! … Pr!) xP1 xP2 … xPr
Where P1 + P2 + P3 + … + Pr = n and 0 ≤ P1, P2, … Pr ≥ n
Number of Terms in the Expansion of (x1 + x2 + … + xr)n
From the general term of the above expansion, we can conclude that the number of terms is equal to the number of ways different powers can be distributed to x1, x2, x3 …., xn, such that the sum of powers is always “n”.
The number of non-negative integral solutions of x1 + x2 + … + xr = n is n +r – 1Cr – 1.
For example, the number of terms in the expansion of (x + y + z)3 is 3 + 3 -1C3 – 1 = 5C2 = 10
As in the expansion, we have terms such as
As x0 y0 z0, x0 y1 z2, x0 y2 z1, x0 y3 z0, x1 y0 z2, x1 y1 z1, x1 y2 z0, x2 y0 z1, x2 y1 z0, x3 y0 z0.
The number of terms in (x + y + z)n is n + 3 – 1C3 – 1 = n + 2C2.
The number of terms in (x + y + z + w)n is n + 4 – 1C4 – 1 = n + 3C3 and so on.
Binomial Theorem IIT JEE Video Lesson

Binomial Coefficients with G.P. or A.P.

Binomial Theorem – Top 12 Most Important and Expected Questions

Problems on Binomial Theorem
Question 1: If the third term in the binomial expansion of  equals 2560, find x.
equals 2560, find x.
Solution:

⇒ (log2x)2 = 4
⇒ log2x = 2 or -2
⇒ x = 4 or 1/4.
Question 2: Find the positive value of λ for which the coefficient of x2 in the expression x2[√x + (λ/x2)]10 is 720.
Solution:
⇒ x2 [10Cr . (√x)10-r . (λ/x2)r] = x2 [10Cr . λr . x(10-r)/2 . x-2r]
= x2 [10Cr . λr . x(10-5r)/2]
Therefore, r = 2
Hence, 10C2 . λ2 = 720
⇒ λ2 = 16
⇒ λ = ±4.
Question 3: The sum of the real values of x for which the middle term in the binomial expansion of (x3/3 + 3/x)8 equals 5670 is?
Solution:
T5 = 8C4 × (x12/81) × (81/x4) = 5670
⇒ 70 x8 = 5670
⇒ x = ± √3.
Question 4: Let (x + 10)50 + (x – 10)50 = a0 +a1x + a2 x2 + . . . . . + a50 x50 for all x ∈R, then a2/a0 is equal to?
Solution:
⇒ (x + 10)50 + (x – 10)50:
a2 = 2 × 50C2 × 1048
a0 = 2 × 1050
⇒ a2/a0 = 50C2/102 = 12.25.
Question 5: Find the coefficient of x9 in the expansion of (1 + x) (1 + x2 ) (1 + x3) . . . . . . (1 + x100).
Solution:
x9 can be formed in 8 ways.
i.e., x9 x1+8 x2+7 x3+6 x4+5, x1+3+5, x2+3+4
∴ The coefficient of x9 = 1 + 1 + 1 + . . . . + 8 times = 8.
Question 6: The coefficients of three consecutive terms of (1 + x)n+5 are in the ratio 5:10:14. Find n.
Solution:
Let Tr-1, Tr, Tr+1 are three consecutive terms of (1 + x)n+5
⇒ Tr-1 = (n+5) Cr-2 . xr-2
⇒ Tr = (n+5) Cr-1 . xr-1
⇒ Tr+1 = (n+5) Cr . xr
Given
(n+5) Cr-2 : (n+5) Cr-1 : (n+5) Cr = 5 : 10 : 14
Therefore, [(n+5) Cr-2]/5= [(n+5) Cr-1]/10 = (n+5) Cr/14
Comparing first two results we have n – 3r = -9 . . . . . . (1)
Comparing last two results we have 5n – 12r = -30 . . . . . . (2)
From equations (1) and (2), n = 6
Question 7: The digit in the units place of the number 183! + 3183.
Solution:
⇒ 3183 = (34)45.33
⇒ unit digit = 7 and 183! ends with 0
∴ The units digit of 183! + 3183 is 7.
Question 8: Find the total number of terms in the expansion of (x + a)100 + (x – a)100.
Solution:
⇒ (x + a)100 + (x – a)100 = 2[100C0 x100. 100C2 x98 . a2 + . . . . . . + 100C100 a100]
∴ Total Terms = 51
Question 9: Find the coefficient of t4 in the expansion of [(1-t6)/(1 – t)].
Solution:
⇒ [(1-t6)/(1 – t)] = (1 – t18 – 3t6 + 3t12) (1 – t)-3
Coefficient of t in (1 – t)-3 = 3 + 4 – 1
C4 = 6C2 =15
The coefficient of xr in (1 – x)-n = (r + n – 1) Cr
Question 10: Find the ratio of the 5th term from the beginning to the 5th term from the end in the binomial expansion of [21/3 + 1/{2.(3)1/3}]10.
Solution:

Question 11: Find the coefficient of a3b2c4d in the expansion of (a-b-c+d)10.
Solution:
Expand (a – b – c + d)10 using the multinomial theorem, and by using the coefficient property, we can obtain the required result.
Using the multinomial theorem, we have

We want to get coefficient of a3b2c4d this implies that r1 = 3, r2 = 2, r3 = 4, r4 = 1,
∴ The coefficient of a3b2c4d is [(10)!/(3!.2!.4)] (-1)2 (-1)-4 = 12600
Question 12: Find the coefficient of in the expansion of (1 + x + x2 +x3)11.
Solution:
By expanding the given equation using the expansion formula, we can get the coefficient x4
i.e. 1 + x + x2 + x3 = (1 + x) + x2 (1 + x) = (1 + x) (1 + x2)
⇒ (1 + x + x2 + x3) x11 = (1+x)11 (1+x2)11
= 1+ 11C1 x2 + 11C2 x2 + 11C3 x3 + 11C4 x4 . . . . . . .
= 1 + 11C1 x2 + 11C2 x4 + . . . . . .
To find the term in from the product of two brackets on the right-hand-side, consider the following products terms as
= 1 × 11C2 x4 + 11C2 x2 × 11C1 x2 + 11C4 x4
= 11C2 + 11C2 × 11C1 + 11C4 ] x4
⇒ [55 + 605 + 330] x4 = 990x4
∴ The coefficient of x4 is 990.
Question 13: Find the number of terms free from the radical sign in the expansion of (√5 + 4√n)100.
Solution:
Tr+1 = 100Cr . 5(100 – r)/2 nr/4
Where r = 0, 1, 2, . . . . . . , 100
r must be 0, 4, 8, … 100
The number of rational terms = 26
Question 14: Find the degree of the polynomial [x + {√(3(3-1))}1/2]5 + [x + {√(3(3-1))}1/2]5.
Solution:
[x + { √(3(3-1)) }1/2 ]5:
= 2 [5C0 x5 + 5C2 x5 (x3 – 1) + 5C4 . x . (x3 – 1)2]
Therefore, the highest power = 7.
Question 15: Find the last three digits of 2726.
Solution:
By reducing 2726 into the form (730 – 1)n and using simple binomial expansion, we will get the required digits.
We have 272 = 729
Now 2726 = (729)13 = (730 – 1)13
= 13C0 (730)13 – 13C1 (730)12 + 13C2 (730)11 – . . . . . – 13C10 (730)3 + 13C11(730)2 – 13C12 (730) + 1
= 1000m + [(13 × 12)]/2] × (14)2 – (13) × (730) + 1
Where ‘m’ is a positive integer
= 1000m + 15288 – 9490 = 1000m + 5799
Thus, the last three digits of 17256 are 799.
Binomial Theorem JEE Solution

Binomial Theorem – Important Topics

Binomial Theorem – Important Questions

Frequently Asked Questions
Give the binomial theorem formula.
We use the binomial theorem to find the expansion of the algebraic terms of the form(x + y)n. The formula is (x + y)n = Σr=0n nCr xn – r · yr.
What is the general term in a binomial expansion?
The general term of a binomial expansion is Tr+1 = nCr xn-r yr.
What is the number of terms in the expansion of (x + a)n + (x-a)n ?
The number of terms in the expansion of (x + a)n + (x-a)n is (n+2)/2 if n is even or (n+1)/2 if n is odd.
List two applications of the binomial theorem.
In Mathematics, the binomial theorem is used to find the remainder and also find the digits of a number.

Comments