Ceva’s theorem is a theorem regarding triangles in Euclidean Plane Geometry. Consider a triangle ABC. Let CE, BG and AF be a cevians that forms a concurrent point i.e. D.
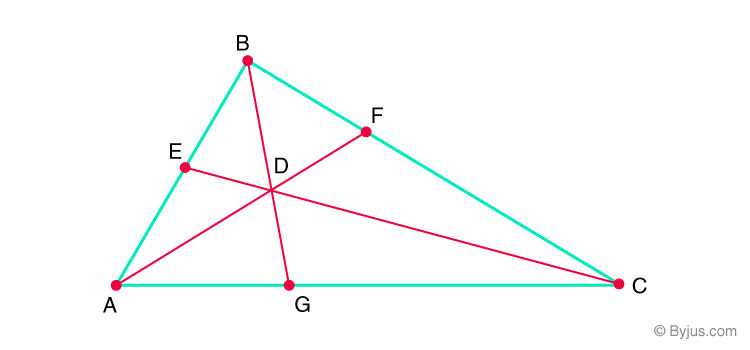
Ceva’s Theorem Statement
Then according to Ceva’s theorem,
\(\begin{array}{l}\large\frac{AG}{GC} \times \frac{CF}{FB}\times\frac{BE}{EA}=1\end{array} \)
Also, the converse of the above is true, i.e. if \(\begin{array}{l}\large\frac{AG}{GC} \times \frac{CF}{FB}\times\frac{BE}{EA}=1\end{array} \)
, then the line AF, BG, CE forms a concurrent point at D.
Ceva’s Theorem Proof
Let h1 and h2 be the altitudes of triangles ABG, BGC and ADG, GDC, respectively. Let the area of the triangle be denoted using closed square brackets such as [ABG], [BGC], and so on.
When h1 and h2 are constructed, [BGC] is equal to 0.5(GC)(h1) and [ABG] is equal to 0.5(AG)(h1). [DGC] is equal to 0.5 (GC)(h2) and [ADG] is equal to 0.5 (AG)(h2).
That means,
\(\begin{array}{l}\frac{0.5\times AG\times h_1}{05\times GC\times h_1}=\frac{[ABG]}{[BGC]}\end{array} \)
And
\(\begin{array}{l}\frac{0.5\times AG\times h_1}{05\times GC\times h_1}=\frac{[ADG]}{[DGC]}\end{array} \)
On simplification we have,
\(\begin{array}{l}\frac{AG}{GC}=\frac{[ABG]}{[BGC]}….(i)\\ \frac{AG}{GC}=\frac{[ADG]}{[DGC]}….(ii)\end{array} \)
From (i) and (ii),
\(\begin{array}{l}\frac{AG}{GC}=\frac{[ABG]}{[BGC]}=\frac{[ADG]}{[DGC]}\end{array} \)
Similarly we can get,
\(\begin{array}{l}\frac{AG}{GC}=\frac{[BDA]}{[BDC]}\\\frac{CF}{FB}=\frac{[ADC]}{[BDA]}\\\frac{BE}{EA}=\frac{[BDC]}{[ADC]}\end{array} \)
Multiplying all these three equations we get,
\(\begin{array}{l}\frac{AG}{GC}\times \frac{CF}{FB}\times \frac{BE}{EA}=\frac{[BDA]}{[BDC]}\times \frac{[ADC]}{[BDA]}\times \frac{[BDC]}{[ADC]}\end{array} \)
On simplification,
\(\begin{array}{l}\frac{AG}{GC}\times \frac{CF}{FB}\times \frac{BE}{EA}=1\end{array} \)
Converse of Ceva’s Theorem

We have,
\(\begin{array}{l}\frac{(AG)}{(GC)}\frac{(CF)}{(AB)}\frac{(BE)}{(EA)}=1\end{array} \)
Here CE, BG, and AF Cevians are concurrent.
Estimate that Cevians CE and AF intersect at D and assume that the Cevians passing through D is BH. So according to Cevians Theorem we have,
\(\begin{array}{l}\frac{AH}{HC}\frac{CF}{FB}\frac{BE}{EA}=1\end{array} \)
As assumed
\(\begin{array}{l}\frac{AG}{GC}\frac{CF}{FB}\frac{BE}{EA}=1\end{array} \)
According to Transitive Property, we have
\(\begin{array}{l}\frac{AH}{HC}\frac{CF}{FB}\frac{BE}{EA}=\frac{AG}{GC}\frac{CF}{FB}\frac{BE}{EA}\end{array} \)
By simplifying
\(\begin{array}{l}\frac{AH}{HC}=\frac{AG}{GC}\end{array} \)
<
It holds true when H and G illustrate the same point. Hence BG, CE, and AF should be concurrent.


Comments