A convex set is defined as a set of points in which the line AB connecting any two points A, B in the set lies completely within that set. Now, let us discuss the definition of convex sets, and other definitions, such as convex hull, convex combinations and solved examples in detail.
Table of Contents:
- Convex Sets Definition
- Extreme and Non-extreme Points of Convex Sets
- Convex Combination
- Convex Hull
- Examples
- FAQs
Convex Sets Definition
A convex set is a collection of points in which the line AB connecting any two points A, B in the set lies completely within the set. In other words, A subset S of En is considered to be convex if any linear combination θx1 + (1 − θ)x2, (0 ≤ θ ≤ 1) is also included in S for all pairs of x1, x2 ∈ S.

What is a Non-convex Set?
Non-convex sets are those that are not convex. A non-convex polygon is occasionally referred to as a concave polygon, and also some sources use the phrase concave set to refer to a non-convex set.
Extreme and Non-extreme Points of Convex Sets
Now, consider the below figure which represents the extreme and non-extreme points of convex sets.
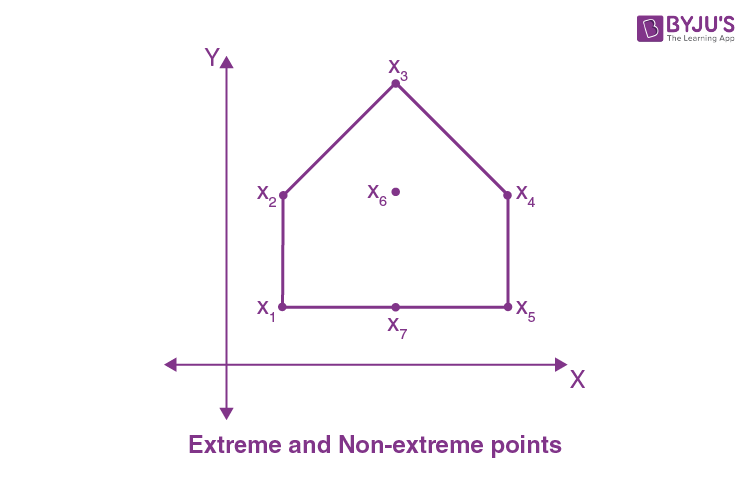
It is noted that the points x1, x2, x3, x4 and x5 are extreme points of convex set S, whereas x6 and x7 are the non-extreme points of the convex set.
Thus, The extreme point or vertex of a convex set S is a point x that does not fall on any line segment connecting any two unique points in S, such as x1 and x2.
Convex Combinations
A convex combination of the finite number of points x1, x2, …, xk is defined as a point
x = θ1x1 + θ2x2 + … + θkxk ,
where θ1 +θ2 …+ θk = 1 and θi ≥ 0 for all i = 1, …, k.
Hence, we can say that a set is convex iff, it contains every convex combination of its points.
What is Convex Hull?
The shortest convex set that contains x is called a convex hull. In other words, if S is a set of vectors in En, then the convex hull of S is the set of all convex combinations of every finite subset of S, and it is represented as [S].

| Also, read: |
Convex Sets Examples
Example 1:
Prove that C = {(x1, x2) : 2x1 + 3x2 = 7} ⊂ R2 is a convex set.
Solution:
Assume that X, Y ∈ C, where X = (x1, x2), Y = (y1, y2). The line segment connecting X and Y is the set.
From the definition of convex sets, we can write the following:
W = {W : W = θX + (1 − θ)Y, 0 ≤ θ ≤ 1}
For some 0 ≤ θ ≤ 1, assume that W = (w1, w2) is the point of set W.
Hence, we can write
w1 = θx1 + (1 − θ)y1
w2 = θx2 + (1 − θ)y2
As x, y ∈ C, we can write
2x1 + 3x2 = 7, and
2y1 + 3y2 = 7
But, from the formula,
2w1 + 3w2 = 2[θx1 + (1 − θ)y1] + 3[θx2 + (1 − θ)y2]
Now, take the common terms outside, we get
= θ[2x1 + 3x2] + (1 − θ)[2y1 + 3y2]
= θ.7 + (1 − θ).7 = 7. [Since 2x1 + 3x2 = 7]
Hence, W = (w1, w2) belongs to C Since W is any point of C, and X, Y ∈ C
This can be written as [X: Y ] ⊂ C.
Therefore, set C is convex.
Example 2:
Prove that the set B = {(x1, x2, x3) : 2x1 − x2 + x3 ≤ 4} ⊂ R3 is a convex set.
Solution:
Assume that X = (x1, x2, x3) and Y = (y1, y2, y3) are the two points of B.
From the given conditions, we can write
2x1 − x2 + x3 ≤ 4
2y1 − y2 + y3 ≤ 4
Now, assume that W = (w1, w2, w3) is any point of [X, Y ] such that 0 ≤ θ ≤ 1,
w1 = θx1 + (1 − θ)y1
w2 = θx2 + (1 − θ)y2
w3 = θx3 + (1 − θ)y3
Using the above equations, we can write
2w1 − w2 + w3 = θ(2x1 − x2 + x3) + (1 − θ)(2y1 − y2 + y3) ≤ 4θ + 4(1 − θ) = 4
Thus, W = (w1, w2, w3) is a point of S.
Therefore, X, Y belongs to B, and hence [X; Y ] ⊂ B.
Hence, the set B is a convex set.
Video Lesson on What are Sets

Frequently Asked Questions on Convex Sets
What is meant by convex set?
A convex set is a collection of points in which the line AB connecting any two points A, B in the set lies completely within the set.
What is a non-convex set?
Non-convex sets are those that are not convex. In other words, the phrase concave set refers to a non-convex set.
What is meant by a convex hull?
The shortest convex set that contains x is called a convex hull
Comments