Two lines are said to be coplanar when they both lie on the same plane in a three-dimensional space. We have learnt how to represent the equation of a line in three-dimensional space using vector notations. In this article, we will learn about the coplanarity of two lines in 3D geometry.
Condition for coplanarity of two lines in vector form
Using vector notations equation of line is given by:
\(\begin{array}{l}\vec{r}\end{array} \)
= \(\begin{array}{l}\vec{l_{1}}\end{array} \)
+ λ\(\begin{array}{l}\vec{m_{1}}\end{array} \)
——————— (1)
\(\begin{array}{l}\vec{r}\end{array} \)
= \(\begin{array}{l}\vec{l_{2}}\end{array} \)
+ μ\(\begin{array}{l}\vec{m_{2}}\end{array} \)
——————– (2)
Here, the line (1) passes through a point L having position vector \(\begin{array}{l}\vec{l_{1}}\end{array} \)
and is parallel to \(\begin{array}{l}\vec{m_{1}}\end{array} \)
and the line (2) passes through a point M having position vector \(\begin{array}{l}\vec{l_{2}}\end{array} \)
and is parallel to \(\begin{array}{l}\vec{m_{2}}\end{array} \)
. These two lines are coplanar if and only if \(\begin{array}{l}\vec{LM}\end{array} \)
is perpendicular to \(\begin{array}{l}\vec{m_{1}}\end{array} \)
x \(\begin{array}{l}\vec{m_{2}}\end{array} \)
.
This can be given as:
\(\begin{array}{l}\vec{LM}\end{array} \)
= \(\begin{array}{l}\vec{l_{2}}\end{array} \)
– \(\begin{array}{l}\vec{l_{1}}\end{array} \)
Thus condition of coplanarity is given by:
\(\begin{array}{l}\vec{LM}\end{array} \)
.(\(\begin{array}{l}\vec{m_{1}}\end{array} \)
x \(\begin{array}{l}\vec{m_{2}}\end{array} \)
) = 0
(\(\begin{array}{l}\vec{l_{2}}\end{array} \)
– \(\begin{array}{l}\vec{l_{1}}\end{array} \)
).(\(\begin{array}{l}\vec{m_{1}}\end{array} \)
x \(\begin{array}{l}\vec{m_{2}}\end{array} \)
) = 0
Condition for coplanarity of two lines in cartesian form
Let us take two points L and M such that (x1, y1, z1) and (x2, y2, z2) be the coordinates of the points respectively. The direction cosines of two vectors \(\begin{array}{l}\vec{m_{1}}\end{array} \)
and \(\begin{array}{l}\vec{m_{2}}\end{array} \)
is given by a1, b1, c1 and a2, b2, c2 respectively.
\(\begin{array}{l}\vec{LM}\end{array} \)
= (x2 − x1)\(\begin{array}{l}\hat{i}\end{array} \)
+ (y2 − y1)\(\begin{array}{l}\hat{j}\end{array} \)
+ (z2 − z1)\(\begin{array}{l}\hat{k}\end{array} \)
\(\begin{array}{l}\vec{m_{1}}\end{array} \)
= a1\(\begin{array}{l}\hat{i}\end{array} \)
+b1\(\begin{array}{l}\hat{j}\end{array} \)
+ c1\(\begin{array}{l}\hat{k}\end{array} \)
\(\begin{array}{l}\vec{m_{2}}\end{array} \)
= a2\(\begin{array}{l}\hat{i}\end{array} \)
+b2\(\begin{array}{l}\hat{j}\end{array} \)
+ c2\(\begin{array}{l}\hat{k}\end{array} \)
By the above condition two lines can be coplanar if and only if,
\(\begin{array}{l}\vec{LM}\end{array} \)
.(\(\begin{array}{l}\vec{m_{1}}\end{array} \)
x \(\begin{array}{l}\vec{m_{2}}\end{array} \)
) = 0
Examples
Question: Show that lines \(\begin{array}{l}\frac{x + 3}{-3}\end{array} \)
= \(\begin{array}{l}\frac{y – 2}{4}\end{array} \)
= \(\begin{array}{l}\frac{z – 5}{5}\end{array} \)
and \(\begin{array}{l}\frac{x + 1}{-3}\end{array} \)
= \(\begin{array}{l}\frac{y – 2}{3}\end{array} \)
= \(\begin{array}{l}\frac{z + 5}{6}\end{array} \)
are coplanar.
Solution:
According to the question:
x1 = -3, y1 = 2, z1 = 5, x2 = -1 , y2 = 2, z2 = -5, a1 = -3 , b1 = 4, c1 = 5, a2 = -3 , b2 = 3, c2 = 6
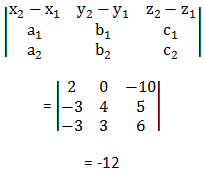
Thus, the given lines are not coplanar. To learn more about coplanarity of two lines download BYJU’S- The Learning App.
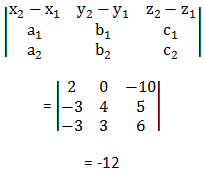
Comments