Functions are relations where each input has a particular output. This lesson covers the concepts of functions in Mathematics and the different types of functions using various examples for better understanding.
Download Complete Chapter Notes of Relations and Functions II
Download Now
Contents Related to Functions
JEE Main 2021 Maths LIVE Paper Solutions 24-Feb Shift-1 Memory-based

What Are Functions in Mathematics?
A function is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. Let A & B be any two non-empty sets; mapping from A to B will be a function only when every element in set A has one end and only one image in set B.
Example:
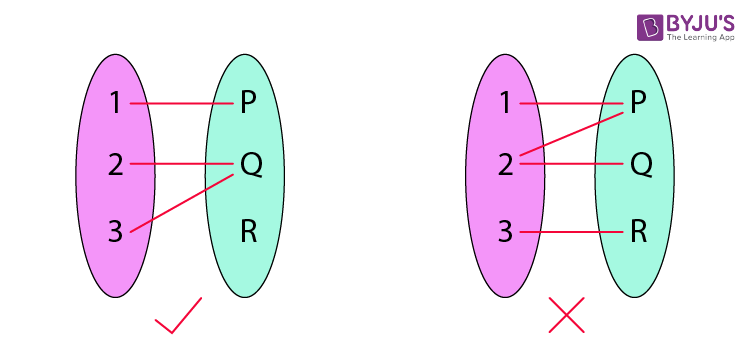
Another definition of functions is that it is a relation “f” in which each element of set “A” is mapped with only one element belonging to set “B”. Also, in a function, there can’t be two pairs with the same first element.
Condition for a Function
Set A and Set B should be non-empty.
In a function, a particular input is given to get a particular output. So, a function f: A->B denotes that f is a function from A to B, where A is a domain, and B is a co-domain.
- For an element, a, which belongs to A, a ∈ A, a unique element b, b ∈ B is there such that (a,b) ∈ f.
The unique element b to which f relates a is denoted by f(a) and is called f of a, or the value of f at a, or the image of a under f.
- The range of f (image of a under f)
- It is the set of all values of f(x) taken together.
- Range of f = { y ∈ Y | y = f (x), for some x in X}
A real-valued function has either P or any one of its subsets as its range. Further, if its domain is also either P or a subset of P, it is called a real function.
Vertical Line Test:
A vertical line test is used to determine whether a curve is a function or not. If any curve cuts a vertical line at more than one point, then the curve is not a function.

Representation of Functions
Functions are generally represented as f(x).
Let , f(x) = x3.
It is said as f of x is equal to x cube.
Functions can also be represented by g(), t(),… etc.
Steps for Solving Functions
Question: Find the output of the function g(t) = 6t2 + 5 at
(i) t = 0
(ii) t = 2
Solution:
The given function is g(t) = 6t2 + 5
(i) At t = 0, g(0) = 6(0)2 + 5 = 5
(ii) At t = 2, g(2) = 6(2)2 + 5 = 29
Types of Functions
There are various types of functions in Mathematics which are explained below in detail. The different function types covered here are given below:
- One-one Function (Injective Function)
- Many-one Function
- Onto Function (Surjective Function)
- Into Function
- Polynomial Function
- Linear Function
- Identical Function
- Quadratic Function
- Rational Function
- Algebraic Functions
- Cubic Function
- Modulus Function
- Signum Function
- Greatest Integer Function
- Fractional Part Function
- Even and Odd Function
- Periodic Function
- Composite Function
- Constant Function
- Identity Function
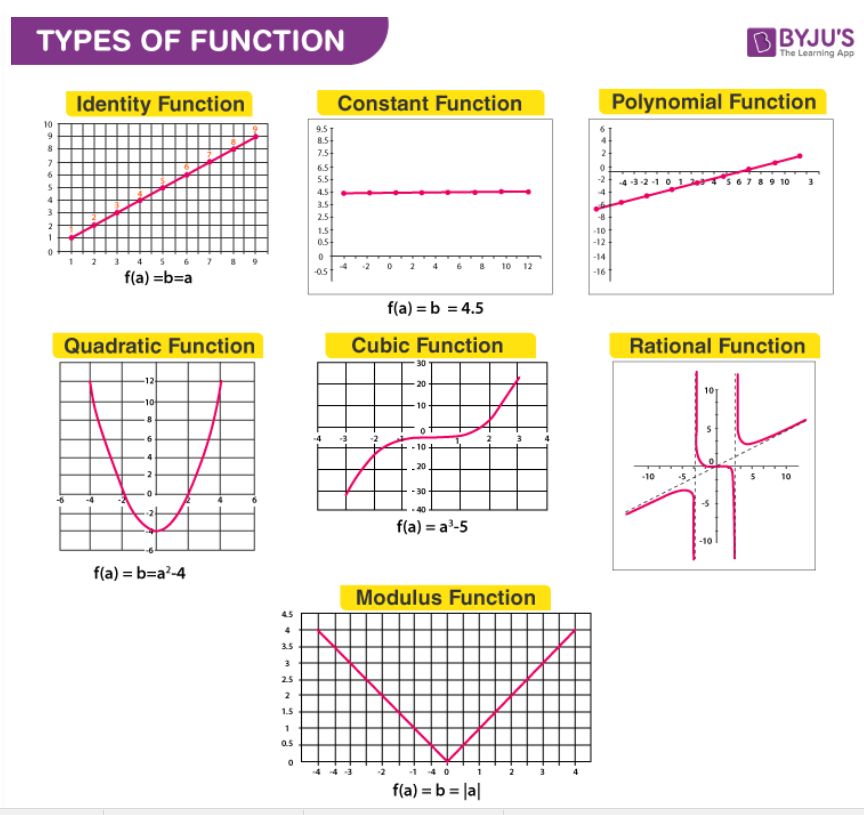
Practice: Find the missing equations from the above graphs.
Functions – Video Lessons
Functions and Types of Functions

Number of Functions

Even and Odd Functions

Composite and Periodic Functions

One-one Function (Injective Function)
If each element in the domain of a function has a distinct image in the co-domain, the function is said to be a one-one function.

For example, f; R R, given by f(x) = 3x + 5, is one-one.
Many-one function
On the other hand, if there are at least two elements in the domain whose images are the same, the function is known as many to one.

For example, f : R R, given by f(x) = x2 + 1, is many-one.
Onto Function (Surjective Function)
A function is called an onto function if each element in the co-domain has at least one pre-image in the domain.
Into Function
If there exists at least one element in the co-domain, which is not an image of any element in the domain, then the function will be into function.
(Q) Let A = {x : 1 < x < 1} = B be a mapping f : A B; find the nature of the given function (P). F(x) = |x|
 f (x) = |1|
f (x) = |1|
Solution for x = 1 & -1
Hence, it is many one, the range of f(x) from [-1, 1] is [0, 1] is not equal to the co-domain.
Hence, it is into function.

Let’s say we have the function,
For different values of the input, we have different outputs; hence it is a one-one function, and also, it manages equally to its co-domain; hence, it is onto also.
Polynomial function
A real-valued function f : P → P defined by
- N = a non-negative integer.
- The degree of the polynomial function is the highest power in the expression.
- If the degree is zero, it’s called a constant function.
- If the degree is one, it’s called a linear function. For example, b = a+1.
- Graph type: Always a straight line.
So, a polynomial function can be expressed as:
The highest power in the expression is known as the degree of the polynomial function. The different types of polynomial functions based on the degree are as follows:
- The polynomial function is called a constant function if the degree is zero.
- The polynomial function is called a linear if the degree is one.
- The polynomial function is quadratic if the degree is two.
- The polynomial function is cubic if the degree is three.
Linear Function
All functions in the form of ax + b where a, b ∈ R & a ≠ 0 are called linear functions. The graph will be a straight line. In other words, a linear polynomial function is a first-degree polynomial where the input needs to be multiplied by m and added to c. It can be expressed by f(x) = mx + c.
For example, f(x) = 2x + 1 at x = 1
f(1) = 2.1 + 1 = 3
f(1) = 3

Another example of a linear function is y = x + 3

Identical Function
Two functions, f and g, are said to be identical if
(a) The domain of f = domain of g
(b) The range of f = the range of g
(c) f(x) = g(x) ∀ x ∈ Df & Dg
For example, f(x) = x
Solution: f(x) = x is defined for all x
But
Hence, it is identical for x ∈ R – {0}
Quadratic Function
All functions in the form of y = ax2 + bx + c where a, b, c ∈ R, a ≠ 0 will be known as Quadratic functions. The graph will be parabolic.

In simpler terms,
A quadratic polynomial function is a second-degree polynomial, and it can be expressed as:
F(x) = ax2 + bx + c, and a is not equal to zero.
Where a, b, and c are constant, and x is a variable.
Example, f(x) = 2x2 + x – 1 at x = 2
If x = 2, f(2) = 2.22 + 2 – 1 = 9
For example, y = x2

Read More: Quadratic Function Formula
Rational Function
These are the real functions of the type
- For example, f : P – {– 6} → P defined by \(\begin{array}{l}f(a) = \frac{f(a+1)}{g(a+2)}\forall a\in P – {-6},\end{array} \)is a rational function.
- Graph type: Asymptotes (the curves touching the axes lines).
Algebraic Functions
An algebraic equation is known as a function that consists of a finite number of terms involving powers and roots of independent variable x and fundamental operations, such as addition, subtraction, multiplication and division.
For example,
Cubic Function
A cubic polynomial function is a polynomial of degree three and can be expressed as:
F(x) = ax3 + bx2 + cx + d, and a is not equal to zero.

In other words, any function in the form of f(x) = ax3 + bx2 + cx + d, where a, b, c, d ∈ R & a ≠ 0

For example, y = x3
Domain ∈ R
Range ∈ R
Modulus Function
The real function f : P → P defined by f (a) = |a| = a when a ≥ 0. and f(a) = -a when a < 0 ∀ a ∈ P is called the modulus function.
- Domain of f = P
- Range of f = P+ U {0}
Domain: R
Range: [0, ∞)
Signum Function
The real function f : P → P is defined by
is called the signum function or sign function (gives the sign of real number).
- Domain of f = P
- Range of f = {1, 0, – 1}
For example, signum (100) = 1
signum (log 1) = 0
signum (x21) =1
Greatest Integer Function

The real function f : P → P defined by f (a) = [a], a ∈ P assumes the value of the greatest integer less than or equal to a is called the greatest integer function.
- Thus f (a) = [a] = – 1 for – 1 ⩽ a < 0
- f (a) = [a] = 0 for 0 ⩽ a < 1
- [a] = 1 for 1 ⩽ a < 2
- [a] = 2 for 2 ⩽ a < 3 and so on…
The greatest integer function always gives integral output. The greatest integral value that has been taken by the input will be the output.
For example, [4.5] = 4
[6.99] = 6 [1.2] = 2Domain ∈ R
Range ∈ Integers
Fractional Part Function

{x} = x – [x]
It always gives fractional value as output.
For example, {4.5} = 4.5 – [4.5]
= 4.5 – 4 = 0.5
{6.99} = 6.99 – [6.99]
= 6.99 – 6 = 0.99
{7} = 7 – [7] = 7 –7 = 0
Even and Odd Function
If f(x) = f(-x), then the function will be even function, and if f(x) = -f(-x), then the function will be odd function.
Example 1:
f(x) = x2sinx
f(-x) = -x2sinx
Here, f(x) = -f(-x)
It is an odd function.
Example 2:
and
f(x) = f(-x)
It is an even function.
Periodic Function
A function is said to be a periodic function if a positive real number T exists, such that f(u – t) = f(x) for all x ε domain.
For example, f(x) = sin x
f(x + 2π) = sin (x + 2π) = sin x fundamental
Then period of sin x is 2π.
Composite Function
Let A, B, and C be three non-empty sets
Let f: A → B & g : G → C be two functions, then gof : A → C. This function is called the composition of f and g given gof (x) = g(f(x)).
For example, f(x) = x2 & g(x) = 2x
f(g(x)) = f(2,x) = (2x)2 = 4x2
g(f(x)) = g(x2) = 2x2
Constant Function
The function f : P → P is defined by b = f (x) = D, a ∈ P, where D is a constant ∈ P, is a constant function.
- Domain of f = P
- Range of f = {D}
- Graph type: A straight line which is parallel to the x-axis.
In simple words, the polynomial of 0th degree where f(x) = f(0) = a0 = c. Regardless of the input, the output always results in a constant value. The graph for this is a horizontal line.

Identity Function
P= set of real numbers
The function f : P → P defined by b = f (a) = a for each a ∈ P is called the identity function.
- Domain of f = P
- Range of f = P
- Graph type: A straight line passing through the origin.
Functions Video
Domain, Range, Period of Functions

Functions and Relations

Relations and Functions Questions

One-One and Onto Functions

Frequently Asked Questions
What do you mean by a function in Mathematics?
A relation f from set A to set B is called a function if every element of set A has one and only one image in set B.
What do you mean by domain of a function?
The domain of a function is the set of all possible inputs for a function.
What do you mean by range of a function?
The range of a function is the set of all possible output values.
What do you mean by a constant function?
Constant function is a function whose output is the same for every input value. For example, f(x) = 3. Here, for every value of x, output will be 3.

good site recommended from me