The HCF of 20, 28 and 36 is 4. The largest positive integer that divides the given numbers without leaving a remainder is defined as the Highest Common Factor (HCF). The article HCF of Two Numbers provides a detailed explanation of the HCF concept. This concept is one of the most vital concepts that students must grasp thoroughly right from the beginning to secure more marks in their academics. 1, 2 and 4 are the common factors of 20, 28 and 36. Thus, 4 is the Highest Common Factor of 20, 28 and 36. Let us learn the tricks to find the Highest Common Factor of 20, 28 and 36 using different methods here.
What is the HCF of 20, 28 and 36?
The Highest Common Factor (HCF) or the Greatest Common Divisor (GCD) of 20, 28 and 36 is 4. Factors of 20 are 1, 2, 4, 5, 10, 20, factors of 28 are 1, 2, 4, 7, 14, 28, and the factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, 36. Clearly, 4 is the Highest Common Factor of 20, 28 and 36.
How to Find HCF of 20, 28 and 36?
There are three methods to find the HCF of 20, 28 and 36:
- Prime Factorisation
- Long Division method
- Listing common factors
HCF of 20, 28 and 36 by Prime Factorisation Method
In the prime factorisation method, we need to express the given numbers as the product of prime factors to find the Highest Common Factor.
20 = 2 × 2 × 5
28 = 2 × 2 × 7
36 = 2 × 2 × 3 × 3
The common prime factors of 20, 28 and 36 are 2 and 2.
Therefore,
HCF (20, 28, 36) = 2 × 2 = 4
HCF of 20, 28 and 36 by Long Division Method
Go through the steps given below to find the Highest Common Factor of 20, 28 and 36 in the long division method.
Step 1: Divide the number 28 by 20. We get the divisor as 4 when the remainder is equal to zero. Hence, the HCF of 20 and 28 is 4.
Step 2: Now, find the HCF of 4 and 36 by performing the long division method on 36 and 4.
Step 3: We get the divisor as 4 when the remainder becomes zero. Therefore, the HCF of 4 and 36 is 4.
The HCF of 20, 28 and 36 by the long division method is shown below:
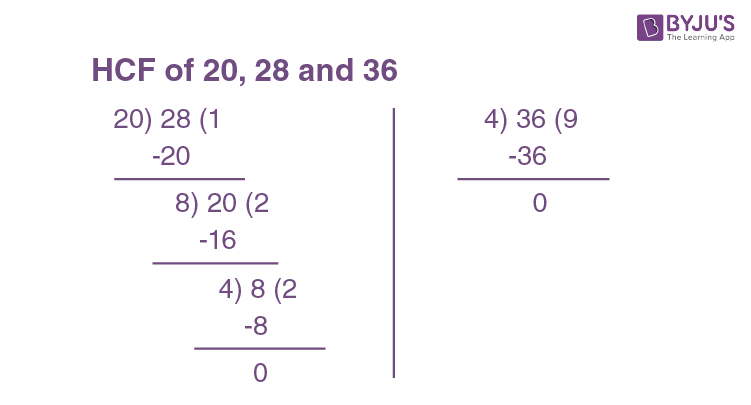
HCF (20, 28) = 4 and HCF (4, 36) = 4
Hence, HCF of (20, 28, 36) = 4
HCF of 20, 28 and 36 by Listing Common Factors
In this method, to find the HCF, we list out all the factors of given numbers and then pick the largest of all the common factors. The factors of 20, 28 and 36 are as follows:
Factors of 20:1, 2, 4, 5, 10, 20
Factors of 28: 1, 2, 4, 7, 14, 28
Factors of 36: 1, 2, 3, 4,6, 9, 12, 18, 36
Hence, HCF (20, 28, 36) = 4
Related Articles
Video Lesson on Properties of HCF and LCM

Solved Example
Question: What is the highest number that divides 20, 28 and 36 exactly?
Solution: The highest number that divides the numbers 20, 28 and 36 is their Highest Common Factor. The factors of 20, 28 and 36 are:
Factors of 20: 1, 2, 4, 5, 10, 20
Factors of 28: 1, 2, 4, 7, 14, 28
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Here, the Highest Common Factor of 20, 28 and 36 is 4. Therefore, 4 is the highest number that divides 20, 28 and 36 exactly.
Frequently Asked Questions on HCF of 20, 28 and 36
What is the HCF of 20, 28 and 36?
Is the HCF of 20, 28 and 36 same as the HCF of 4, 16 and 32?
Mention the methods used to find the HCF of 20, 28 and 36.
The methods used to find the HCF of 20, 28 and 36 are:
Prime Factorisation
Long Division method
Listing common factors
Calculate the HCF of 20, 28 and 36 using prime factorisation.
To find the HCF using prime factorisation, we write the given numbers as the product of prime factors.
20 = 2 × 2 × 5
28 = 2 × 2 × 7
36 = 2 × 2 × 3 × 3
The common prime factors of 20, 28 and 36 are 2 and 2
Therefore, HCF (20, 28, 36) = 2 × 2 = 4
Comments