Highest Common Factor

The Highest Common Factor (HCF) of two or more numbers is the greatest of all their common factors. Therefore, it is also called the greatest common factor (GCF). If we say M is the highest common factor of N, then M is the highest possible number that divides the number N.

For example, the common factors of 12 and 16 are 1, 2 and 4. But the highest common factor of 12 and 16 will be 4, which is common to both the numbers.

In this article, we will learn to find the HCF of two or more numbers along with examples in simple ways. Class 6 students will be able to excel in the concept of the highest common factor by reading this article.

Learn more: HCF

Highest Common Factor Meaning

The highest common factor is also known as the greatest common factor (GCF) or the greatest common divisor (GCD). 

Highest Common Factor Formula

There is no exact formula for finding the highest common factor of given numbers. However, we can write the statement that helps to find the greatest common factor of two or more numbers when considering the prime factorization. 

HCF = Product of the smallest power of each common prime factor in the numbers

Also, check: HCF of Two Numbers

How to Find the Highest Common Factor?

Different methods are defined to calculate the highest common factor of the given numbers. Three techniques that are frequently used to calculate the HCF of two or more numbers in mathematics are:

• HCF by listing factors method
• HCF by prime factorization method
• HCF by division method

Let’s learn all these methods with the help of an example in each case.

Finding HCF by Listing Factors

In this method, we need to list the factors of the given numbers and then pick the largest of all the common factors.

Example: Highest common factor of 32 and 24

Solution:

Factors of 32 = 1, 2, 4, 8, 16, 32

Factors of 24 = 1, 2, 3, 4, 6, 8, 12, 24

Here, the largest number that is common in the list of factors is 8.

Therefore, HCF(32, 24) = 8.

Get the factors of 32 and factors of 24 here.

Finding HCF by Prime Factorization 

The greatest common factor of given numbers can be found by the prime factorization method. Here, we need to express the given numbers as their product of prime factors and get the product of the smallest power of each common prime factor. Let’s understand this procedure with the help of an example given below:

Example: Highest common factor of 36 and 84

Solution:

Prime factorization of 36 = 2 × 2 × 3 × 3 = 2² × 3²

Prime factorization of 84 = 2 × 2 × 3 × 7 = 2² × 3 × 7

Thus, the highest common factor of 36 and 84 = 2² × 3 = 4 × 3 = 12

HCF(36, 84) = 12

Finding HCF by Division Method

The division method of finding the highest common factor is simple and can be performed quickly. Go through the steps given below to find the HCF of the given two numbers using division.

Step 1: Divide the largest number by the smallest one among the given two numbers.

Step 2: Check the remainder, if it is not 0, then make it a new divisor and write the previous divisor as the new dividend. Then perform division.

Step 3: Continue this process until we get the remainder equal to 0. Also, the last divisor will be the HCF of the given two numbers.

Let’s have a look at the example given below for a better understanding of this method.

Example: Highest common factor of 18 and 24

Solution:

24 > 18

So, dividend = 24 and divisor = 18

Let’s perform the division as explained in the above steps.

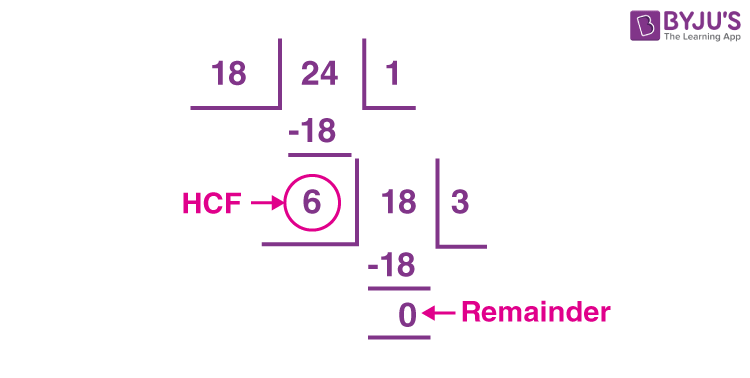
Therefore, the highest common factor of 18 and 24 is 6.

Also, try: GCF Calculator

Solved Examples

Q.1: Find the HCF of the following numbers:

(a) 30, 104

(b) 15, 25, 72

Solution:

(a) 30, 104

By prime factorisation of 30 and 104, we get;

Factors of 30 → 1, 2, 3, 5, 6, 10, 15, 30

Factors of 104 → 1, 2, 4, 8, 13, 26, 52, 104

As we can see, among all the factors, 2 is the only highest common factor for 30 and 104.

Therefore, HCF (30, 104) = 2

(b) 15, 25, 75

By prime factorisation of 15, 25 and 75, we get;

Factors of 15 → 1, 3, 5, 15

Factors of 25 → 1, 5, 25

Factors of 75 → 1, 3, 5, 15, 25, 75

Therefore, HCF of (15, 25, 75) = 5

Q.2: What is the GCF of 10, 50 and 100?

Solution:

By prime factorisation, we can list the prime factors of 10, 50 and 100, respectively.

Factors of 10 → 1, 2, 5, 10

Factors of 50 → 1, 2, 5, 10, 25, 50

Factors of 100 → 1, 2, 4, 5, 10, 20, 25, 50, 100

Therefore, the HCF of (10, 50, 100) = 10.