Linear equations in two variables, explain the geometry of lines or the graph of two lines, plotted to solve the given equations. As we already know, the linear equation represents a straight line. The plotting of these graphs will help us to solve the equations, which consist of unknown variables. Previously we have learned to solve linear equations in one variable, here we will find the solutions for the equations having two variables.
| Table of contents: |
Definition
An equation is said to be linear equation in two variables if it is written in the form of ax + by + c=0, where a, b & c are real numbers and the coefficients of x and y, i.e a and b respectively, are not equal to zero.
For example, 10x+4y = 3 and -x+5y = 2 are linear equations in two variables.
The solution for such an equation is a pair of values, one for x and one for y which further makes the two sides of an equation equal.
Also, read:
Solution of Linear Equations in Two Variables
The solution of linear equations in two variables, ax+by = c, is a particular point in the graph, such that when x-coordinate is multiplied by a and y-coordinate is multiplied by b, then the sum of these two values will be equal to c.
Basically, for linear equation in two variables, there are infinitely many solutions.
Example
In order to find the solution of Linear equation in 2 variables, two equations should be known to us.
Consider for Example:
5x + 3y = 30
The above equation has two variables namely x and y.
Graphically this equation can be represented by substituting the variables to zero.
The value of x when y=0 is
5x + 3(0) = 30
⇒ x = 6
and the value of y when x = 0 is,
5 (0) + 3y = 30
⇒ y = 10
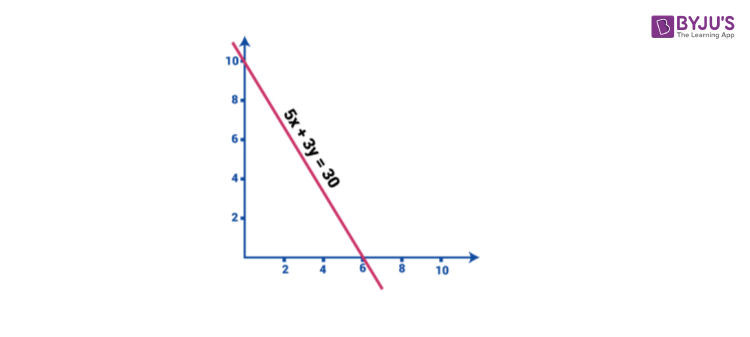
It is now understood that to solve linear equation in two variables, the two equations have to be known and then the substitution method can be followed. Let’s understand this with a few example questions.
Unique Solution
For the given linear equations in two variables, the solution will be unique for both the equations, if and only if they intersect at a single point.
The condition to get the unique solution for the given linear equations is, the slope of the line formed by the two equations, respectively, should not be equal.
Consider, m1 and m2 are two slopes of equations of two lines in two variables. So, if the equations have a unique solution, then:
No Solution
If the two linear equations have equal slope value, then the equations will have no solutions.
m1 = m2
This is because the lines are parallel to each other and do not intersect.
System of Linear Equations in Two Variables
Instead of finding the solution for a single linear equation in two variables, we can take two sets of linear equations, both having two variables in them and find the solutions. So, basically the system of linear equations is defined when there is more than one linear equation.
For example, a+b = 15 and a-b = 5, are the system of linear equations in two variables. Because, the point a = 10 and b = 5 is the solution for both equations, such as:
a+b=10 + 5 = 15
a-b=10-5 = 5
Hence, proved point (10,5) is solution for both a+b=15 and a-b=5.
Problems and Solutions
Question: Find the value of variables which satisfies the following equation:
2x + 5y = 20 and 3x+6y =12.
Solution:
Using the method of substitution to solve the pair of linear equation, we have:
2x + 5y = 20…………………….(i)
3x+6y =12……………………..(ii)
Multiplying equation (i) by 3 and (ii) by 2, we have:
6x + 15y = 60…………………….(iii)
6x+12y = 24……………………..(iv)
Subtracting equation (iv) from (iii)
3y = 36
⇒ y = 12
Substituting the value of y in any of the equation (i) or (ii), we have
2x + 5(12) = 20
⇒ x = −20
Therefore, x=-20 and y =12 is the point where the given equations intersect.
Now, it is important to know the situational examples which are also known as word problems from linear equations in 2 variables.
Check: Linear Equations Calculator
Word Problems
Question 1: A boat running downstream covers a distance of 20 km in 2 hours while for covering the same distance upstream, it takes 5 hours. What is the speed of the boat in still water?
Solution:
These types of questions are the real-time examples of linear equations in two variables.
In water, the direction along the stream is called downstream. And, the direction against the stream is called upstream.
Let us consider the speed of a boat is u km/h and the speed of the stream is v km/h, then:
Speed Downstream = (u + v) km/h
Speed Upstream = (u – v) km/h
We know that, Speed = Distance/Time
So, the speed of boat when running downstream = (20⁄2) km/h = 10 km/h
The speed of boat when running upstream = (20⁄5) km/h = 4 km/h
From above, u + v = 10…….(1)
u – v = 4 ………. (2)
Adding equation 1 and 2, we get: 2u = 1
u = 7 km/h
Also, v = 3 km/h
Therefore, the speed of the boat in still water = u = 7 km/h
Question 2: A boat running upstream takes 6 hours 30 minutes to cover a certain distance, while it takes 3 hours to cover the same distance running downstream. What is the ratio between the speed of the boat and speed of the water current, respectively?
Solution: If the speed downstream is a km/hr and the speed upstream is b km/hr, then
Speed in still water = (a + b)/2 km/h
Rate of stream = ½ (a − b) kmph
Let the Boat’s rate upstream be x kmph and that downstream be y kmph.
Then, distance covered upstream in 6 hrs 30 min = Distance covered downstream in 3 hrs.
⇒ x × 6.5 hrs = y × 3hrs
⇒ 13/2x = 3y
⇒ y = 13x/6



Excellent service
excellent job
Helping the students well