Mean deviation questions are given here along with the detailed solutions. Mean deviation can be calculated for the measures of central tendency, such as mean deviation from the mean, and mean deviation about the median. In this article, you can learn how to calculate the mean deviation for the given data using simple calculator steps.
What is the Mean deviation?
As we know, the mean deviation is one of the measures of dispersion in statistics. In mathematical terms, the mean deviation can be defined as the mean of the absolute numerical differences between the observations of a data set and their corresponding mean or median values.
Mean deviation from mean
|
Type of data |
Mean deviation from Mean formula |
Explanation |
|
Ungrouped data |
∑|xi – x̄|/ n |
xi = observations x1, x2, x3,…, xn x̄ = Mean of observations |
|
Discrete data |
∑fi |xi – x̄|/ N |
xi = observations x1, x2, x3,…, xn fi = Frequencies f1, f2, f3,…., fn N = Sum of frequencies |
|
Continuous data |
∑fi |xi – x̄|/ N |
xi = Midpoints of class intervals fi = Frequencies f1, f2, f3,…., fn N = Sum of frequencies |
Mean deviation about median
|
Type of data |
Mean deviation about Median formula |
Explanation |
|
Ungrouped data |
∑|xi – M|/ n |
xi = observations x1, x2, x3,…, xn M = Median of observations |
|
Discrete data |
∑fi |xi – M|/ N |
xi = observations x1, x2, x3,…, xn fi = Frequencies f1, f2, f3,…., fn N = Sum of frequencies |
|
Continuous data |
∑fi |xi – M|/ N |
xi = Midpoints of class intervals fi = Frequencies f1, f2, f3,…., fn N = Sum of frequencies |
Also, read:
Mean Deviation Questions and Answers
1. Find the mean deviation from the mean for the following data set.
57, 64, 43, 67, 49, 59, 44, 47, 61, 59
Solution:
Given,
57, 64, 43, 67, 49, 59, 44, 47, 61, 59
Mean = (57 + 64 + 43 + 67 + 49 + 59 + 44 + 47 + 61 + 59)/10 = 550/10 = 55
|xi – x̄| = |57 – 55|, |64 – 55|,
|43 – 55|,
|67 – 55|, |49 – 55|, |59 – 55|, |44 – 55|, |47 – 55|, |61 – 55|, |59 – 55|
= 2, 9, 12, 12, 6, 4, 11, 8, 6, 4
Mean deviation = ∑|xi – x̄|/ n
= (2 + 9 + 12 + 12 + 6 + 4 + 11 + 8 + 6 + 4)/10
= 74/10
= 7.4
Therefore, the mean deviation of the given data is 7.4.
2. Calculate the mean deviation about the mean of the set of the first 10 natural numbers.
Solution:
First 10 natural numbers: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Mean = (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10)/10
= 55/10
= 5.5
|xi – x̄| = |1 – 5.5|, |2 – 5.5|, |3 – 5.5|, |4 – 5.5|, |5 – 5.5|, |6 – 5.5|, |7 – 5.5|, |8 – 5.5|, |9 – 5.5|, |10 – 5.5|
= 4.5, 3.5, 2.5, 1.5, 0.5, 0.5, 1.5, 2.5, 3.5, 4.5
Mean deviation = ∑|xi – x̄|/ n
= (4.5 + 3.5 + 2.5 + 1.5 + 0.5 + 0.5 + 1.5 + 2.5 + 3.5 + 4.5)/10
= 25/10
= 2.5
Thus, the mean deviation about the mean for the first 10 natural numbers is 2.5.
3. Find the mean deviation about the median for the following data.
6, 15, 4, 10, 12, 11, 5, 3, 16
Solution:
Given,
6, 15, 4, 10, 12, 11, 5, 3, 16
Ascending order of the given data is: 3, 4, 5, 6, 10, 11, 12, 15, 16
Number of data values = 9
Median = (n + 1)/2 th observation
= (9 + 1)/2
= 5th observation
Median (M) = 10
The absolute values of the respective deviations from the median, i.e., |xi − M| are:
|3 – 10|, |4 – 10|, |5 – 10|, |6 – 10|, |10 – 10|, |11 – 10|, |12 – 10|, |15 – 10|, |16 – 10|
= 7, 6, 5, 4, 0, 1, 2, 5, 6
Mean deviation = ∑|xi – M|/ n
= (7 + 6 + 5 + 4 + 0 + 1 + 2 + 5 + 6)/9
= 36/9
= 4
Hence, the mean deviation about median for the given data is 4.
4. Calculate the mean deviation from mean for the following distribution.
|
x |
1 |
3 |
4 |
5 |
6 |
7 |
|
f |
4 |
9 |
16 |
14 |
11 |
6 |
Solution:
|
xi |
1 |
3 |
4 |
5 |
6 |
7 |
|
fi |
4 |
9 |
16 |
14 |
11 |
6 |
|
fx |
4 |
27 |
64 |
70 |
66 |
42 |
|
|xi – x̄| |
3.55 |
1.55 |
0.55 |
0.45 |
1.45 |
2.45 |
|
fi |xi – x̄| |
14.2 |
13.95 |
8.8 |
6.3 |
15.95 |
17.15 |
Mean (x̄) = ∑fixi/∑fi
= (4 + 27 + 64 + 70 + 66 + 42)/ (4 + 9 + 16 + 14 + 11 + 6)
= 273/60
= 4.55
Mean deviation = ∑fi |xi – x̄|/ N
= (14.2 + 13.95 + 8.8 + 6.3 + 15.95 + 17.15)/60
= 76.35/60
= 1.2725
Therefore, the mean deviation from the mean for the given discrete data is 1.2725.
5. Calculate the mean deviation about the mean of the set of first n natural numbers when n is an even number.
Solution:
Natural numbers are: 1, 2, 3, 4, 5,…., n (even)
Sum of these natural numbers = n(n + 1)/2
Mean (x̄) = [n(n + 1)/2]/ n = (n + 1)/2
Mean deviation =
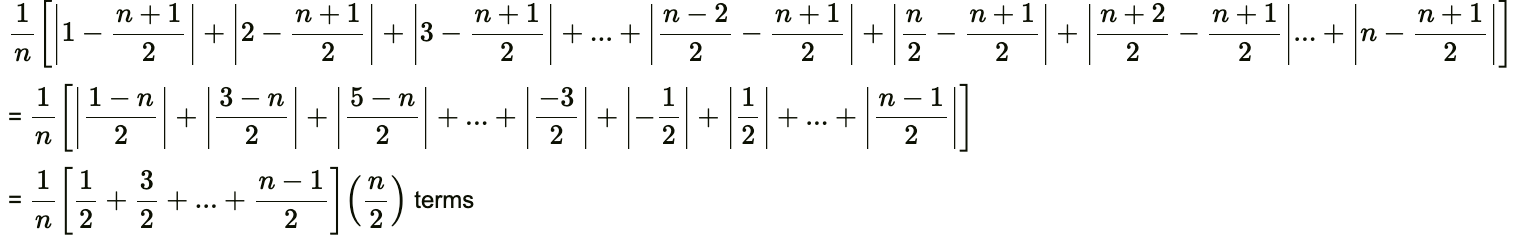
= (1/n) (n/2)2
= n/4
6. Find the mean deviation about the median for the following data.
|
Marks |
20 |
29 |
28 |
33 |
42 |
38 |
43 |
25 |
|
Number of students |
6 |
28 |
24 |
15 |
2 |
4 |
1 |
20 |
Solution:
Let us write the given data in an ascending order and calculate the cumulative frequency for the same, as follows:
|
Marks (xi) |
20 |
25 |
28 |
29 |
33 |
38 |
42 |
43 |
|
Number of students (fi) |
6 |
20 |
24 |
28 |
15 |
4 |
2 |
1 |
|
Cumulative frequency |
6 |
26 |
50 |
78 |
93 |
97 |
99 |
100 |
Here, N = 100
Median = (28 + 29)/2 = 28.5
The absolute values of the respective deviations from the median, i.e., |xi − M| are:
|20 – 28.5|, |25 – 28.5|, |28 – 28.5|, |29 – 28.5|, |33 – 28.5|, |38 – 28.5|, |42 – 28.5|, |43 – 28.5|
= 8.5, 3.5, 0.5, 0.5, 4.5, 9.5, 13.5, 14.5
Mean deviation = ∑fi|xi – M|/ N
= [6(8.5) + 20(3.5) + 24(0.5) + 28(0.5) + 15(4.5) + 4(9.5) + 2(13.5) + 1(14.5)]/ 100
= 294/100
= 2.94
Therefore, the mean deviation about median of the given data is 2.94.
7. Calculate the mean deviation about the mean for the following frequency distribution:
|
Classes |
0 – 4 |
4 – 8 |
8 – 12 |
12 – 16 |
16 – 20 |
|
Frequency |
4 |
6 |
8 |
5 |
2 |
Solution:
|
Classes |
Frequency (fi) |
Mid values (xi) |
fixi |
|xi – x̄| |
fi |xi – x̄| |
|
0 – 4 |
4 |
2 |
8 |
7.2 |
28.8 |
|
4 – 8 |
6 |
6 |
36 |
3.2 |
19.2 |
|
8 – 12 |
8 |
10 |
80 |
0.8 |
6.4 |
|
12 – 16 |
5 |
14 |
70 |
4.8 |
24 |
|
16 – 20 |
2 |
18 |
36 |
8.8 |
17.6 |
|
∑fi = 25 |
∑fixi = 230 |
∑fi |xi – x̄| = 96 |
Mean (x̄) = ∑fixi/∑fi
= 230/25
= 9.2
Mean deviation = ∑fi |xi – x̄|/N
= 96/25
= 3.84
8. Calculate the mean deviation from the mean of the following continuous data.
|
Class |
10 – 20 |
20 – 30 |
30 – 50 |
50 – 70 |
70 – 80 |
Total |
|
Frequency |
5 |
8 |
16 |
8 |
3 |
40 |
Solution:
|
Class |
Frequency |
Midvalue (xi) |
fixi |
|xi – x̄| |
fi |xi – x̄| |
|
10 – 20 |
5 |
15 |
75 |
25.5 |
127.5 |
|
20 – 30 |
8 |
25 |
200 |
15.5 |
124 |
|
30 – 50 |
16 |
40 |
640 |
0.5 |
8 |
|
50 – 70 |
8 |
60 |
480 |
19.5 |
156 |
|
70 – 80 |
3 |
75 |
225 |
34.5 |
103.5 |
|
∑fi = 40 |
∑fixi = 1620 |
∑fi |xi – x̄| = 519 |
Mean (x̄) = ∑fixi/∑fi
= 1620/40
= 40.5
Mean deviation = ∑fi |xi – x̄|/N
= 519/40
= 12.975
9. Calculate the mean deviation about the median for the following data.
|
xi |
3 |
6 |
9 |
12 |
13 |
15 |
21 |
22 |
|
fi |
3 |
4 |
5 |
2 |
4 |
5 |
4 |
3 |
Solution:
|
xi |
3 |
6 |
9 |
12 |
13 |
15 |
21 |
22 |
|
fi |
3 |
4 |
5 |
2 |
4 |
5 |
4 |
3 |
|
Cumulative frequency |
3 |
7 |
12 |
14 |
18 |
23 |
27 |
30 |
|
|xi – M| |
10 |
7 |
4 |
1 |
0 |
2 |
8 |
9 |
|
fi |xi – M| |
30 |
28 |
20 |
2 |
0 |
10 |
32 |
27 |
N = 30 (even)
N/2 = 15
Median = (15th observation + 16th observation)/2
= (13 + 13)/2
= 13
Mean deviation = ∑fi|xi – M|/ N
= (30 + 28 + 20 + 2 + 0 + 10 + 32 + 27)/30
= 149/30
= 4.97
10. Estimate the mean deviation about median for the following data.
|
Classes |
0 – 10 |
10 – 20 |
20 – 30 |
30 – 40 |
40 – 50 |
50 – 60 |
|
Frequency |
11 |
30 |
17 |
4 |
5 |
3 |
Solution:
|
Classes |
0 – 10 |
10 – 20 |
20 – 30 |
30 – 40 |
40 – 50 |
50 – 60 |
|
Frequency |
11 |
30 |
17 |
4 |
5 |
3 |
|
Midvalues (xi) |
5 |
15 |
25 |
35 |
45 |
55 |
|
Cumulative frequency |
11 |
41 |
58 |
62 |
67 |
70 |
Here, N = 70
N/2 = 70/2 = 35
Cumulative frequency greater than and nearer to 35 is 41, which lies in the class interval 10 – 20.
Median class = 10 – 20
l = Lower limit of the median class = 10
f = Frequency of the median class = 30
cf = Cumulative frequency preceding the median class = 11
h = Class height = 10
Median = l +h [(N/2) – cf]/f
= 10 + 10 × [(35 – 11)/30]
= 10 + (24 × 10/30)
= 10 + 8
= 18
The absolute values of the respective deviations from the median, i.e., |xi − M| are:
|5 – 18|, |15 – 18|, |25 – 18|, |35 – 18|, |45 – 18|, |55 – 18|
= 7, 3, 7, 17, 27, 37
Mean deviation = ∑fi|xi – M|/ N
= [11(7) + 30(3) + 17(7) + 4(17) + 5(27) + 3(37)]/ 70
= 600/70
= 8.57 (approx)
Practice Questions on Mean Deviation
- Calculate the mean deviation from the mean of the following data set.
50, 69, 20, 33, 53, 39, 40, 65, 59 - What is the mean deviation about the median for the given data values 25, 50, 45, 30, 70, 42, 36, 48, 35, 60?
- Calculate the mean deviation from the mean for the given data.
- Calculate the mean deviation about the mean of the set of first n natural numbers when n is an odd number.
- Find the mean deviation from mean and median for the first 10 even natural numbers.
|
x |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
15 |
|
f |
3 |
3 |
4 |
14 |
7 |
4 |
3 |
4 |