Polynomials are algebraic expressions that consist of variables and coefficients. Variables are also sometimes called indeterminates. We can perform arithmetic operations such as addition, subtraction, multiplication, and also positive integer exponents for polynomial expressions but not division by variable. An example of a polynomial with one variable is x2+x-12. In this example, there are three terms: x2, x and -12.

Also, Check: What is Mathematics
The word polynomial is derived from the Greek words ‘poly’ means ‘many‘ and ‘nominal’ means ‘terms‘, so altogether it is said as “many terms”. A polynomial can have any number of terms but not infinite. Let’s learn about the degrees, terms, types, properties, and polynomial functions in this article.
| Table of Contents: |
What is a Polynomial?
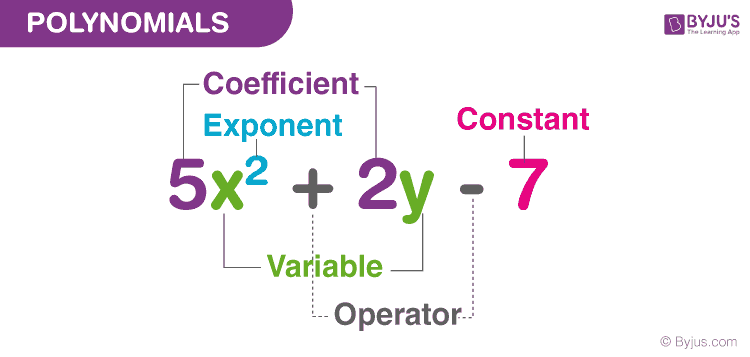
Polynomial is made up of two terms, namely Poly (meaning “many”) and Nominal (meaning “terms.”). A polynomial is defined as an expression which is composed of variables, constants and exponents, that are combined using mathematical operations such as addition, subtraction, multiplication and division (No division operation by a variable). Based on the number of terms present in the expression, it is classified as monomial, binomial, and trinomial. Examples of constants, variables and exponents are as follows:
- Constants. Example: 1, 2, 3, etc.
- Variables. Example: g, h, x, y, etc.
- Exponents: Example: 5 in x5 etc.
Standard Form of a Polynomial
P(x) = anxn + an-1xn-1 +an-2xn-2 + ………………. + a1x + a0
Where an, an-1, an-2, ……………………, a1, a0 are called coefficients of xn, xn-1, xn-2, ….., x and constant term respectively and it should belong to real number (⋲ R).
Notation
The polynomial function is denoted by P(x) where x represents the variable. For example,
P(x) = x2-5x+11
If the variable is denoted by a, then the function will be P(a)
Degree of a Polynomial
The degree of a polynomial is defined as the highest exponent of a monomial within a polynomial. Thus, a polynomial equation having one variable which has the largest exponent is called a degree of the polynomial.
| Polynomial | Degree | Example |
|---|---|---|
| Zero Polynomial | Not Defined | 6 |
| Constant | 0 | P(x) = 6 |
| Linear Polynomial | 1 | P(x) = 3x+1 |
| Quadratic Polynomial | 2 | P(x) = 4x2+1x+1 |
| Cubic Polynomial | 3 | P(x) = 6x3+4x2+3x+1 |
| Quartic Polynomial | 4 | P(x) = 6x4+3x3+3x2+2x+1 |
Example: Find the degree of the polynomial P(x) = 6s4+ 3x2+ 5x +19
Solution:
The degree of the polynomial is 4 as the highest power of the variable 4.
Terms of a Polynomial
The terms of polynomials are the parts of the expression that are generally separated by “+” or “-” signs. So, each part of a polynomial in an expression is a term. For example, in a polynomial, say, 2x2 + 5 +4, the number of terms will be 3. The classification of a polynomial is done based on the number of terms in it.
| Polynomial | Terms | Degree |
| P(x) = x3-2x2+3x+4 | x3, -2x2, 3x and 4 | 3 |
Types of Polynomials
Depending upon the number of terms, polynomials are divided into the following categories:
- Monomial
- Binomial
- Trinomial
- Polynomial containing 4 terms (Quadronomial)
- Polynomial containing 5 terms (pentanomial ) and so on …
These polynomials can be combined using addition, subtraction, multiplication, and division but is never divided by a variable. A few examples of Non Polynomials are: 1/x+2, x-3
Monomial
A monomial is an expression which contains only one term. For an expression to be a monomial, the single term should be a non-zero term. A few examples of monomials are:
- 5x
- 3
- 6a4
- -3xy
Binomial
A binomial is a polynomial expression which contains exactly two terms. A binomial can be considered as a sum or difference between two or more monomials. A few examples of binomials are:
- – 5x+3,
- 6a4 + 17x
- xy2+xy
Trinomial
A trinomial is an expression which is composed of exactly three terms. A few examples of trinomial expressions are:
- – 8a4+2x+7
- 4x2 + 9x + 7
| Monomial | Binomial | Trinomial |
| One Term | Two terms | Three terms |
| Example: x, 3y, 29, x/2 | Example: x2+x, x3-2x, y+2 | Example: x2+2x+20 |
Properties
Some of the important properties of polynomials along with some important polynomial theorems are as follows:
Property 1: Division Algorithm
If a polynomial P(x) is divided by a polynomial G(x) results in quotient Q(x) with remainder R(x), then,
P(x) = G(x) • Q(x) + R(x)
Where R(x)=0 or the degree of R(x) < the degree of G(x)
Property 2: Bezout’s Theorem
Polynomial P(x) is divisible by binomial (x – a) if and only if P(a) = 0.
Property 3: Remainder Theorem
If P(x) is divided by (x – a) with remainder r, then P(a) = r.
Property 4: Factor Theorem
A polynomial P(x) divided by Q(x) results in R(x) with zero remainders if and only if Q(x) is a factor of P(x).
Learn More: Factor Theorem
Property 5: Intermediate Value Theorem
If P(x) is a polynomial, and P(x) ≠ P(y) for (x < y), then P(x) takes every value from P(x) to P(y) in the closed interval [x, y].
Learn More: Intermediate Value Theorem
Property 6
The addition, subtraction and multiplication of polynomials P and Q result in a polynomial where,
Degree(P ± Q) ≤ Degree(P or Q)
Degree(P × Q) = Degree(P) + Degree(Q)
Property 7
If a polynomial P is divisible by a polynomial Q, then every zero of Q is also a zero of P.
Property 8
If a polynomial P is divisible by two co-prime polynomials Q and R, then it is divisible by (Q • R).
Property 9
If P(x) = a0 + a1x + a2x2 + …… + anxn is a polynomial such that deg(P) = n ≥ 0 then, P has at most “n” distinct roots.
Property 10: Descartes’ Rule of Sign
The number of positive real zeroes in a polynomial function P(x) is the same or less than by an even number as the number of changes in the sign of the coefficients. So, if there are “K” sign changes, the number of roots will be “k” or “(k – a)”, where “a” is some even number.
Property 11: Fundamental Theorem of Algebra
Every non-constant single-variable polynomial with complex coefficients has at least one complex zero.
Property 12
If P(x) is a polynomial with real coefficients and has one complex zero (x = a – bi), then x = a + bi will also be a zero of P(x). Also, x2 – 2ax + a2 + b2 will be a factor of P(x).
Polynomial Equations
Polynomial equations are those expressions which are made up of multiple constants and variables. The standard form of writing a polynomial equation is to put the highest degree first and then, at last, the constant term. An example of a polynomial equation is:
0 = a4 +3a3 -2a2 +a +1
Polynomial Functions
A polynomial function is an expression constructed with one or more terms of variables with constant exponents. If there are real numbers denoted by a, then function with one variable and of degree n can be written as:
| f(x) = a0xn + a1xn-1 + a2xn-2 + ….. + an-2x2 + an-1x + an |
Solving Polynomials
Any polynomial can be easily solved using basic algebra and factorization concepts. While solving the polynomial equation, the first step is to set the right-hand side as 0. The explanation of a polynomial solution is explained in two different ways:
- Solving Linear Polynomials
- Solving Quadratic Polynomials
Solving Linear Polynomials
Getting the solution of linear polynomials is easy and simple. First, isolate the variable term and make the equation as equal to zero. Then solve as basic algebra operation. An example of finding the solution of a linear equation is given below:
Example: Solve 3x – 9
Solution:
First, make the equation as 0. So,
3x – 9 = 0
⇒ 3x = 9
⇒ x = 9/3
Or, x = 3.
Thus, the solution of 3x-9 is x = 3.
Solving Quadratic Polynomials
To solve a quadratic polynomial, first, rewrite the expression in the descending order of degree. Then, equate the equation and perform polynomial factorization to get the solution of the equation. An example to find the solution of a quadratic polynomial is given below for better understanding.
Example: Solve 3x2 – 6x + x3 – 18
Solution:
First, arrange the polynomial in the descending order of degree and equate to zero.
⇒ x3 + 3x2 -6x – 18 = 0
Now, take the common terms.
x2(x+3) – 6(x+3) =0
⇒ (x2-6)(x+3)=0
So, the solutions will be x =-3 or
x2 = 6
Or, x = ±√6
More Polynomials Related Resources:
| Remainder Theorem And Polynomials | Algebraic Expressions |
| Polynomials Worksheets | Zeros Of polynomial |
Polynomial Operations
There are four main polynomial operations which are:
- Addition of Polynomials
- Subtraction of Polynomials
- Multiplication of Polynomials
- Division of Polynomials
Each of the operations on polynomials is explained below using solved examples.
Addition of Polynomials
To add polynomials, always add the like terms, i.e. the terms having the same variable and power. The addition of polynomials always results in a polynomial of the same degree. For example,
Example: Find the sum of two polynomials: 5x3+3x2y+4xy−6y2, 3x2+7x2y−2xy+4xy2−5
Solution:
First, combine the like terms while leaving the unlike terms as they are. Hence,
(5x3+3x2y+4xy−6y2)+(3x2+7x2y−2xy+4xy2−5)
= 5x3+3x2+(3+7)x2y+(4−2)xy+4xy2−6y2−5
= 5x3+3x2+10x2y+2xy+4xy2−6y2−5
Subtraction of Polynomials
Subtracting polynomials is similar to addition, the only difference being the type of operation. So, subtract the like terms to obtain the solution. It should be noted that subtraction of polynomials also results in a polynomial of the same degree.
Example: Find the difference of two polynomials: 5x3+3x2y+4xy−6y2, 3x2+7x2y−2xy+4xy2−5
Solution:
First, combine the like terms while leaving the unlike terms as they are. Hence,
(5x3+3x2y+4xy−6y2)-(3x2+7x2y−2xy+4xy2−5)
= 5x3-3x2+(3-7)x2y+(4+2)xy-4xy2−6y2+5
Multiplication of Polynomials
Two or more polynomial when multiplied always result in a polynomial of higher degree (unless one of them is a constant polynomial). An example of multiplying polynomials is given below:
Example: Solve (6x−3y)×(2x+5y)
Solution:
⇒ 6x ×(2x+5y)–3y × (2x+5y) ———- Using distributive law of multiplication
⇒ (12x2+30xy) – (6yx+15y2) ———- Using distributive law of multiplication
⇒12x2+30xy–6xy–15y2 —————– as xy = yx
Thus, (6x−3y)×(2x+5y)=12x2+24xy−15y2
Division of Polynomials
Division of two polynomial may or may not result in a polynomial. Let us study below the division of polynomials in detail. To divide polynomials, follow the given steps:
Polynomial Division Steps:
If a polynomial has more than one term, we use long division method for the same. Following are the steps for it.
- Write the polynomial in descending order.
- Check the highest power and divide the terms by the same.
- Use the answer in step 2 as the division symbol.
- Now subtract it and bring down the next term.
- Repeat steps 2 to 4 until you have no more terms to carry down.
- Note the final answer, including remainder, will be in the fraction form (last subtract term).
Polynomial Examples
Example:
Given two polynomial 7s3+2s2+3s+9 and 5s2+2s+1.
Solve these using mathematical operation.
Solution:
Given polynomial:
7s3+2s2+3s+9 and 5s2+2s+1
Polynomial Addition: (7s3+2s2+3s+9) + (5s2+2s+1)
= 7s3+(2s2+5s2)+(3s+2s)+(9+1)
= 7s3+7s2+5s+10
Hence, addition result in a polynomial.
Polynomial Subtraction: (7s3+2s2+3s+9) – (5s2+2s+1)
= 7s3+(2s2-5s2)+(3s-2s)+(9-1)
= 7s3-3s2+s+8
Hence addition result in a polynomial.
Polynomial Multiplication:(7s3+2s2+3s+9) × (5s2+2s+1)
= 7s3 (5s2+2s+1)+2s2 (5s2+2s+1)+3s (5s2+2s+1)+9 (5s2+2s+1))
= (35s5+14s4+7s3)+ (10s4+4s3+2s2)+ (15s3+6s2+3s)+(45s2+18s+9)
= 35s5+(14s4+10s4)+(7s3+4s3+15s3)+ (2s2+6s2+45s2)+ (3s+18s)+9
= 35s5+24s4+26s3+ 53s2+ 21s +9
Polynomial Division: (7s3+2s2+3s+9) ÷ (5s2+2s+1)
(7s3+2s2+3s+9)/(5s2+2s+1)
This cannot be simplified. Therefore, division of these polynomial do not result in a Polynomial.
Keep visiting BYJU’S to get more such math lessons on different topics. Also, register now to access numerous video lessons for different math concepts to learn in a more effective and engaging way.
Frequently Asked Questions – FAQs
What is a Polynomial?
What are terms, degrees and exponents in a polynomial?
Terms: 2x2,-3x & 19
Degree: 2 (the highest exponent of variable x)
Exponents: Power raised to variable x, i.e. 2 and 1.
What is the standard form of the polynomial?
What is the degree of zero and constant polynomial?
Is 8 a polynomial?
How to add and subtract polynomials?
For example if we add x2+3x and 2x2 + 2x + 9, then we get:
x2+3x+2x2+2x+9 = 3x2+5x+9. Subtracting polynomials is similar to addition, the only difference being the type of operation. So, subtract the like terms to obtain the solution. It should be noted that subtraction of polynomials also results in a polynomial of the same degree.
So,
x2+3x-(2x2+2x+9) = x2+3x-2x2-2x-9 = -x2+x-9


I am doing algebra at school , and I forgot alot about it. therefore I wanna some help
thanks you helped me do my maths exam
It was useful
It’s good it helped me very much for my project
It was useful THANK YOU