Standard Deviation Formula

Before we derive the standard deviation formula let us first understand the meaning of standard deviation. For a set of data, the measure of dispersion, about mean, when expressed as the positive square root of the variance, is called standard deviation. It measures the dispersion or spread of data.

The formula for calculating the standard deviation of given data is:

Standard Deviation Formula

The population standard deviation formula is given as:

Here,

σ = Population standard deviation

N = Number of observations in the population

Xi = ith observation in the population

μ = Population mean

Similarly, the sample standard deviation formula is:

Here,

s = Sample standard deviation

n = Number of observations in the sample

xi = ith observation in the sample

Variance Formula:

The population variance formula is given by:

The sample variance formula is given by:

This is the basic formula for finding the standard deviation for a given set of data.

Standard Deviation For Discrete Data

For discrete frequency distribution of the type:

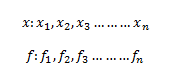
The standard deviation is given as:

where x̄  is the mean of the distribution and

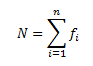
Standard Deviation For Continuous Frequency Distribution

For continuous frequency distribution, the mid-point of each class is considered for calculating the standard deviation. If the frequency distribution of n classes is defined by its mid-point x_i with frequency f_i, the standard deviation is given by:

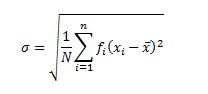
where x_i represents midpoints of the classes and f_i represents the respective frequencies.

And x̄ is the mean of the distribution and

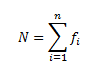
Derivation

Now let us try to obtain another standard deviation formula:

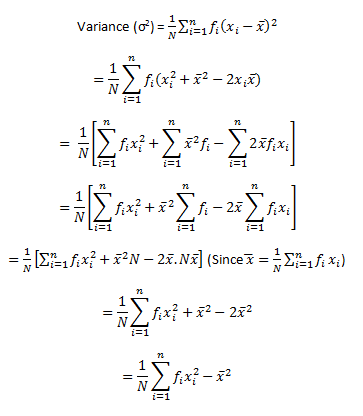
Or,

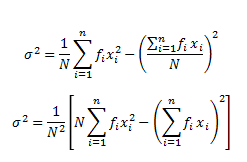
This gives us the standard deviation (σ) as:

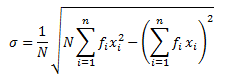
This is the standard deviation formula for a given set of observations. But sometimes, it happens that the value x_i in a given data set or the midpoints of classes in a given frequency distribution is very enormous. In such cases, the determination of mean or median or variance becomes lengthy and time-consuming. To solve this problem, we make use of the step deviation method to simplify the procedure.

Simple Method to Find Standard Deviation

Let us discuss this shortcut method for determining variance and standard deviation.

Consider the assumed mean as ‘A’ and the width of the class interval to be h. Let the step deviation be y_i.

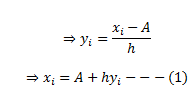
The mean of a data set is given by:

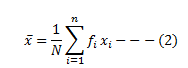
Substituting the values of x_i from equation (1) into equation (2), we get

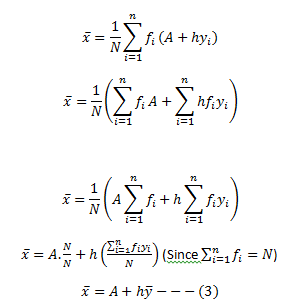
Variance of the variable x,

Substituting the values from equation (1) and (3), we have

σ_x=h² × variance of variable y_i

⇒σ_x²=h²σ_y²

⇒σ_x=hσ_y—(4)

From equation (3) and (4), we can conclude that:

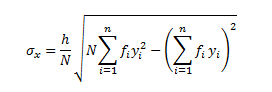
Solved Examples

Let us look into an example for a better insight.

Example 1: Find out the mean, variance and standard deviation for the following data representing the age group of employees working in XYZ Company.

Solution: Let the assumed mean A = 30 and h = 10. From the table given above, we can obtain.

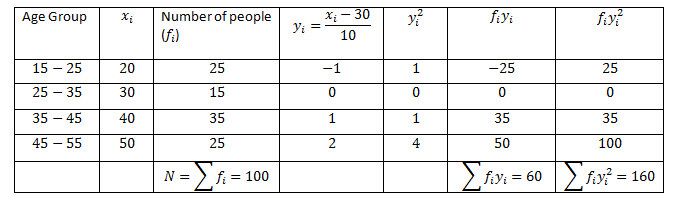
Thus,

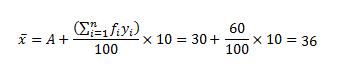
The variance of the above data can be calculated as:

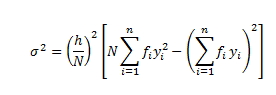
= (10/100)² [100 × 160 – (60)²] = (1/100) [16000 – 3600] = (100/100) [160 – 36] = 124

The standard deviation can be given as:

σ = √124 = 11.136

Example 2: Find the mean, standard deviation and variance for the following data:

57, 64, 43, 67, 49, 59, 44, 47, 61, 59

Solution:

Given,

57, 64, 43, 67, 49, 59, 44, 47, 61, 59

Number of data values = 10

Mean

= 550/10

= 55

Standard variance (σ)

=

=

= √(662/10)

= √66.2

= 8.13

Variance = σ² = 66.2

To learn more concepts of maths, download BYJU’S- The Learning App.