In statistics, the standard error is the standard deviation of the sample distribution. The sample mean of a data is generally varied from the actual population mean. It is represented as SE. It is used to measure the amount of accuracy by which the given sample represents its population. Statistics is a vast topic in which we learn about data, sample and population, mean, median, mode, dependent and independent variables, standard deviation, variance, etc. Here you will learn the standard error formula along with SE of the mean and estimation.
Table of contents:
Standard Error Meaning
The standard error is one of the mathematical tools used in statistics to estimate the variability. It is abbreviated as SE. The standard error of a statistic or an estimate of a parameter is the standard deviation of its sampling distribution. We can define it as an estimate of that standard deviation.
Standard Error Formula
The accuracy of a sample that describes a population is identified through the SE formula. The sample mean which deviates from the given population and that deviation is given as;
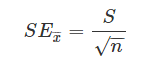
Where S is the standard deviation and n is the number of observations.
Standard Error of the Mean (SEM)
The standard error of the mean also called the standard deviation of mean, is represented as the standard deviation of the measure of the sample mean of the population. It is abbreviated as SEM. For example, normally, the estimator of the population mean is the sample mean. But, if we draw another sample from the same population, it may provide a distinct value.
Thus, there would be a population of the sampled means having its distinct variance and mean. It may be defined as the standard deviation of such sample means of all the possible samples taken from the same given population. SEM defines an estimate of standard deviation which has been computed from the sample. It is calculated as the ratio of the standard deviation to the root of sample size, such as:
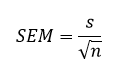 .
.
Where ‘s’ is the standard deviation and n is the number of observations.
The standard error of the mean shows us how the mean changes with different tests, estimating the same quantity. Thus if the outcome of random variations is notable, then the standard error of the mean will have a higher value. But, if there is no change observed in the data points after repeated experiments, then the value of the standard error of the mean will be zero.
Standard Error of Estimate (SEE)
The standard error of the estimate is the estimation of the accuracy of any predictions. It is denoted as SEE. The regression line depreciates the sum of squared deviations of prediction. It is also known as the sum of squares error. SEE is the square root of the average squared deviation. The deviation of some estimates from intended values is given by standard error of estimate formula.
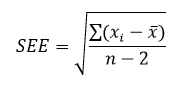
Where xi stands for data values, x bar is the mean value and n is the sample size.
Also check:
How to calculate Standard Error
Step 1: Note the number of measurements (n) and determine the sample mean (μ). It is the average of all the measurements.
Step 2: Determine how much each measurement varies from the mean.
Step 3: Square all the deviations determined in step 2 and add altogether: Σ(xi – μ)²
Step 4: Divide the sum from step 3 by one less than the total number of measurements (n-1).
Step 5: Take the square root of the obtained number, which is the standard deviation (σ).
Step 6: Finally, divide the standard deviation obtained by the square root of the number of measurements (n) to get the standard error of your estimate.
Go through the example given below to understand the method of calculating standard error.
Standard Error Example
Calculate the standard error of the given data:
y: 5, 10, 12, 15, 20
Solution: First we have to find the mean of the given data;
Mean = (5+10+12+15+20)/5 = 62/5 = 10.5
Now, the standard deviation can be calculated as;
S = Summation of difference between each value of given data and the mean value/Number of values.
Hence,
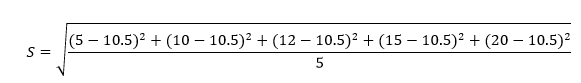
After solving the above equation, we get;
S = 5.35
Therefore, SE can be estimated with the formula;
SE = S/√n
Standard Error vs Standard Deviation
The below table shows how we can calculate the standard deviation (SD) using population parameters and standard error (SE) using sample parameters.
| Population parameters | Formula for SD | Sample statistic | Formula for SE |
| Mean \(\begin{array}{l}\bar{x}\end{array} \) |
\(\begin{array}{l}\frac{\sigma }{\sqrt{n}}\end{array} \) |
Sample mean \(\begin{array}{l}\bar{x}\end{array} \) |
\(\begin{array}{l}\frac{s}{\sqrt{n}}\end{array} \) |
| Sample proportion (P) | \(\begin{array}{l}\sqrt{\frac{P(1-P)}{n}}\end{array} \) |
Sample proportion (p) | \(\begin{array}{l}\sqrt{\frac{p(1-p)}{n}}\end{array} \) |
| Difference between means \(\begin{array}{l}\bar{x_1}-\bar{x_2}\end{array} \) |
\(\begin{array}{l}\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\end{array} \) |
Difference between means
|
\(\begin{array}{l}\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}\end{array} \) |
| Difference between proportions P1 – P2 | \(\begin{array}{l}\sqrt{\frac{P_1(1-P_1)}{n_1}+\frac{P_2(1-P_2)}{n_2}}\end{array} \) |
Difference between proportions p1 – p2 | \(\begin{array}{l}\sqrt{\frac{p_1(1-p_1)}{n_1}+\frac{p_2(1-p_2)}{n_2}}\end{array} \) |
Importance of Standard Error
Standard errors produce simplistic measures of uncertainty in a value. They are often used because, in many cases, if the standard error of some individual quantities is known, then we can easily calculate the standard error of some function of the quantities. Also, when the probability distribution of the value is known, we can use it to calculate an exact confidence interval. However, the standard error is an essential indicator of how precise an estimate of the sample statistic’s population parameter is.