An inverse function or an anti function is defined as a function, which can reverse into another function. In simple words, if any function “f” takes x to y then, the inverse of “f” will take y to x. If the function is denoted by ‘f’ or ‘F’, then the inverse function is denoted by f-1 or F-1. One should not confuse (-1) with exponent or reciprocal here.
| If f and g are inverse functions, then f(x) = y if and only if g(y) = x |
In trigonometry, the inverse sine function is used to find the measure of angle for which sine function generated the value. For example, sin-1(1) = sin-1(sin 90) = 90 degrees. Hence, sin 90 degrees is equal to 1.
Table of Contents:
Definition
A function accepts values, performs particular operations on these values and generates an output. The inverse function agrees with the resultant, operates and reaches back to the original function.
| The inverse function returns the original value for which a function gave the output. |
If you consider functions, f and g are inverse, f(g(x)) = g(f(x)) = x. A function that consists of its inverse fetches the original value.
Example: f(x) = 2x + 5 = y
Then, g(y) = (y-5)/2 = x is the inverse of f(x).
Note:
- The relation, developed when the independent variable is interchanged with the variable which is dependent on a specified equation and this inverse may or may not be a function.
- If the inverse of a function is itself, then it is known as inverse function, denoted by f-1(x).
Inverse Function Graph
The graph of the inverse of a function reflects two things, one is the function and second is the inverse of the function, over the line y = x. This line in the graph passes through the origin and has slope value 1. It can be represented as;
y = f-1(x)
which is equal to;
x = f(y)
This relation is somewhat similar to y = f(x), which defines the graph of f but the part of x and y are reversed here. So if we have to draw the graph of f-1, then we have to switch the positions of x and y in axes.
Video Lesson
Inverse Functions

How to Find the Inverse of a Function?
Generally, the method of calculating an inverse is swapping of coordinates x and y. This newly created inverse is a relation but not necessarily a function.
The original function has to be a one-to-one function to assure that its inverse will also be a function. A function is said to be a one to one function only if every second element corresponds to the first value (values of x and y are used only once).
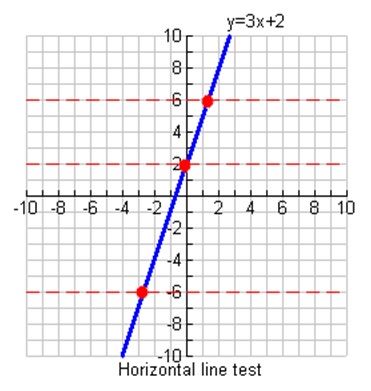
You can apply on the horizontal line test to verify whether a function is a one-to-one function. If a horizontal line intersects the original function in a single region, the function is a one-to-one function and inverse is also a function.
Types of Inverse Function
There are various types of inverse functions like the inverse of trigonometric functions, rational functions, hyperbolic functions and log functions. The inverses of some of the most common functions are given below.
| Function | Inverse of the Function | Comment |
|---|---|---|
| + | – | |
| × | / | Don’t divide by 0 |
| 1/x | 1/y | x and y not equal to 0 |
| x2 | √y | x and y ≥ 0 |
| xn | y1/n | n is not equal to 0 |
| ex | ln(y) | y > 0 |
| ax | log a(y) | y and a > 0 |
| Sin (x) | Sin-1 (y) | – π/2 to + π/2 |
| Cos (x) | Cos-1 (y) | 0 to π |
| Tan (x) | Tan-1 (y) | – π/2 to + π/2 |
Inverse Trigonometric Functions
The inverse trigonometric functions are also known as arc function as they produce the length of the arc, which is required to obtain that particular value. There are six inverse trigonometric functions which include arcsine (sin-1), arccosine (cos-1), arctangent (tan-1), arcsecant (sec-1), arccosecant (cosec-1), and arccotangent (cot-1).
Inverse Rational Function
A rational function is a function of form f(x) = P(x)/Q(x) where Q(x) ≠ 0. To find the inverse of a rational function, follow the following steps. An example is also given below which can help you to understand the concept better.
- Step 1: Replace f(x) = y
- Step 2: Interchange x and y
- Step 3: Solve for y in terms of x
- Step 4: Replace y with f-1(x) and the inverse of the function is obtained.
Inverse Hyperbolic Functions
Just like inverse trigonometric functions, the inverse hyperbolic functions are the inverses of the hyperbolic functions. There are mainly 6 inverse hyperbolic functions exist which include sinh-1, cosh-1, tanh-1, csch-1, coth-1, and sech-1. Check out inverse hyperbolic functions formula to learn more about these functions in detail.
Inverse Logarithmic Functions and Inverse Exponential Function
The natural log functions are inverse of the exponential functions. Check the following example to understand the inverse exponential function and logarithmic function in detail. Also, get more insights of how to solve similar questions and thus, develop problem-solving skills.
Finding Inverse Function Using Algebra
Put “y” for “f(x)” and solve for x:
| The function: | f(x) | = | 2x+3 |
| Put “y” for “f(x)”: | y | = | 2x+3 |
| Subtract 3 from both sides: | y-3 | = | 2x |
| Divide both sides by 2: | (y-3)/2 | = | x |
| Swap sides: | x | = | (y-3)/2 |
| Solution (put “f-1(y)” for “x”) : | f-1(y) | = | (y-3)/2 |
Inverse Functions Example
Example 1:
Find the inverse of the function f(x) = ln(x – 2)
Solution:
First, replace f(x) with y
So, y = ln(x – 2)
Replace the equation in exponential way , x – 2 = ey
Now, solving for x,
x = 2 + ey
Now, replace x with y and thus, f-1(x) = y = 2 + ey
Example 2:
Solve: f(x) = 2x + 3, at x = 4
Solution:
We have,
f(4) = 2 × 4 + 3
f(4) = 11
Now, let’s apply for reverse on 11.
f-1(11) = (11 – 3) / 2
f-1(11) = 4
Magically we get 4 again.
Therefore, f-1(f(4)) = 4
So, when we apply function f and its reverse f-1 gives the original value back again, i.e, f-1(f(x)) = x.
Example 3:
Find the inverse for the function f(x) = (3x+2)/(x-1)
Solution:
First, replace f(x) with y and the function becomes,
y = (3x+2)/(x-1)
By replacing x with y we get,
x = (3y+2)/(y-1)
Now, solve y in terms of x :
x (y – 1) = 3y + 2
=> xy – x = 3y +2
=> xy – 3y = 2 + x
=> y (x – 3) = 2 + x
=> y = (2 + x) / (x – 3)
So, y = f-1(x) = (x+2)/(x-3)
Download BYJU’S- The Learning App to get a more engaging and effective learning experience.
Frequently Asked Questions – FAQs
What is the inverse function?
How to find the inverse of a function?
Let f(x) = 2x+3 = y
y = 2x+3
x = (y-3)/2 = f-1(y)
This is the inverse of f(x).
Are inverse function and reciprocal of function, same?
For example, f(x) = 2x = y
f-1(y) = y/2 = x, is the inverse of f(x).
But, 1/f(x) = 1/2x = f(x)-1 is the reciprocal of function f(x).
What is the inverse of 1/x?
Then inverse of f(x) will be f-1(y).
f-1(y) = 1/x
How to solve inverse trigonometry function?
As we know, sin 30° = ½.
Therefore, sin x = ½
x = sin-1(½) = sin-1 (sin 30°) = 30°


Comments