NCERT Solutions for Class 9 Maths includes solutions to all the questions given in the NCERT Maths textbook. Each answer to the exercise has been carefully compiled and developed, keeping in consideration the latest CBSE syllabus. The NCERT solutions provide students with a fine preparation strategy to focus on their board exams methodically.
Download free NCERT Solutions for Maths Class 9 Maths Chapter 8 Quadrilaterals Exercise 8.1 questions and answers help students to enhance their confidence and problem-solving skills. NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals are prepared by subject experts in simple and understandable language. Students get extremely accurate and detailed answers to all questions.
NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals Exercise 8.1
Access other exercise solutions of Class 9 Maths Chapter 8 Quadrilaterals
Exercise 8.2 Solutions: 7 Solved Questions
Access Answers of Maths NCERT Class 9 Chapter 8 Quadrilateral Exercise 8.1
1. The angles of a quadrilateral are in the ratio 3:5:9:13. Find all the angles of the quadrilateral.
Solution:
Let the common ratio between the angles be = x.
We know that the sum of the interior angles of the quadrilateral = 360°
Now,
3x+5x+9x+13x = 360°
⇒ 30x = 360°
⇒ x = 12°
Angles of the quadrilateral are:
3x = 3×12° = 36°
5x = 5×12° = 60°
9x = 9×12° = 108°
13x = 13×12° = 156°
2. If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Solution:
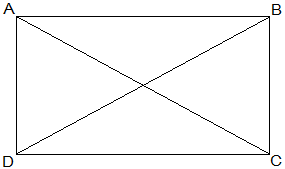
Given that,
AC = BD
To show that ABCD is a rectangle if the diagonals of a parallelogram are equal.
To show ABCD is a rectangle, we have to prove that one of its interior angles is right angled.
Proof,
In ΔABC and ΔBAD,
AB = BA (Common)
BC = AD (Opposite sides of a parallelogram are equal)
AC = BD (Given)
Therefore, ΔABC ≅ ΔBAD [SSS congruency]
∠A = ∠B [Corresponding parts of Congruent Triangles]
also,
∠A+∠B = 180° (Sum of the angles on the same side of the transversal)
⇒ 2∠A = 180°
⇒ ∠A = 90° = ∠B
Therefore, ABCD is a rectangle.
Hence Proved.
3. Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
Solution:
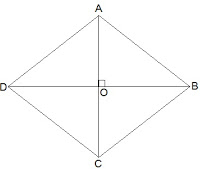
Let ABCD be a quadrilateral whose diagonals bisect each other at right angles.
Given that,
OA = OC
OB = OD
and ∠AOB = ∠BOC = ∠OCD = ∠ODA = 90°
To show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.
i.e., we have to prove that ABCD is a parallelogram and AB = BC = CD = AD
Proof,
In ΔAOB and ΔCOB,
OA = OC (Given)
∠AOB = ∠COB (Opposite sides of a parallelogram are equal)
OB = OB (Common)
Therefore, ΔAOB ≅ ΔCOB [SAS congruency]
Thus, AB = BC [CPCT]
Similarly, we can prove,
BC = CD
CD = AD
AD = AB
AB = BC = CD = AD
Opposite sides of a quadrilateral are equal; hence ABCD is a parallelogram.
ABCD is rhombus as it is a parallelogram whose diagonals intersect at the right angle.
Hence Proved.
4. Show that the diagonals of a square are equal and bisect each other at right angles.
Solution:
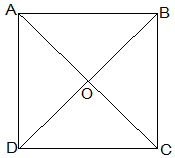
Let ABCD be a square and its diagonals AC and BD intersect each other at O.
To show that,
AC = BD
AO = OC
and ∠AOB = 90°
Proof,
In ΔABC and ΔBAD,
AB = BA (Common)
∠ABC = ∠BAD = 90°
BC = AD (Given)
ΔABC ≅ ΔBAD [SAS congruency]
Thus,
AC = BD [CPCT]
diagonals are equal.
Now,
In ΔAOB and ΔCOD,
∠BAO = ∠DCO (Alternate interior angles)
∠AOB = ∠COD (Vertically opposite)
AB = CD (Given)
ΔAOB ≅ ΔCOD [AAS congruency]
Thus,
AO = CO [CPCT].
Diagonal bisect each other.
Now,
In ΔAOB and ΔCOB,
OB = OB (Given)
AO = CO (diagonals are bisected)
AB = CB (Sides of the square)
ΔAOB ≅ ΔCOB [SSS congruency]
Also, ∠AOB = ∠COB
∠AOB+∠COB = 180° (Linear pair)
Thus, ∠AOB = ∠COB = 90°
Diagonals bisect each other at right angles
5. Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.
Solution:
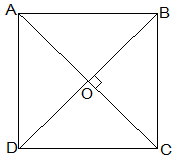
Given that,
Let ABCD be a quadrilateral and its diagonals AC and BD bisect each other at the right angle at O.
To prove that,
The Quadrilateral ABCD is a square.
Proof,
In ΔAOB and ΔCOD,
AO = CO (Diagonals bisect each other)
∠AOB = ∠COD (Vertically opposite)
OB = OD (Diagonals bisect each other)
ΔAOB ≅ ΔCOD [SAS congruency]
Thus,
AB = CD [CPCT] — (i)
also,
∠OAB = ∠OCD (Alternate interior angles)
⇒ AB || CD
Now,
In ΔAOD and ΔCOD,
AO = CO (Diagonals bisect each other)
∠AOD = ∠COD (Vertically opposite)
OD = OD (Common)
ΔAOD ≅ ΔCOD [SAS congruency]
Thus,
AD = CD [CPCT] — (ii)
also,
AD = BC and AD = CD
⇒ AD = BC = CD = AB — (ii)
also, ∠ADC = ∠BCD [CPCT]
and ∠ADC+∠BCD = 180° (co-interior angles)
⇒ 2∠ADC = 180°
⇒∠ADC = 90° — (iii)
One of the interior angles is a right angle.
Thus, from (i), (ii) and (iii), given quadrilateral ABCD is a square.
Hence Proved.
6. Diagonal AC of a parallelogram ABCD bisects ∠A (see Fig. 8.19). Show that
(i) it bisects ∠C
(ii) ABCD is a rhombus.
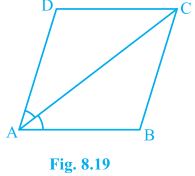
Solution:
(i) In ΔADC and ΔCBA,
AD = CB (Opposite sides of a parallelogram)
DC = BA (Opposite sides of a parallelogram)
AC = CA (Common Side)
ΔADC ≅ ΔCBA [SSS congruency]
Thus,
∠ACD = ∠CAB by CPCT
and ∠CAB = ∠CAD (Given)
⇒ ∠ACD = ∠BCA
Thus,
AC bisects ∠C also.
(ii) ∠ACD = ∠CAD (Proved above)
⇒ AD = CD (Opposite sides of equal angles of a triangle are equal)
Also, AB = BC = CD = DA (Opposite sides of a parallelogram)
Thus,
ABCD is a rhombus.
7. ABCD is a rhombus. Show that diagonal AC bisects ∠A as well as ∠C, and diagonal BD bisects ∠B and ∠D.
Solution:
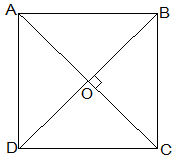
Given that,
ABCD is a rhombus.
AC and BD are its diagonals.
Proof,
AD = CD (Sides of a rhombus)
∠DAC = ∠DCA (Angles opposite of equal sides of a triangle are equal.)
Also, AB || CD
⇒∠DAC = ∠BCA (Alternate interior angles)
⇒∠DCA = ∠BCA, AC bisects ∠C.
Similarly,
We can prove that diagonal AC bisects ∠A.
Following the same method,
We can prove that the diagonal BD bisects ∠B and ∠D.
8. ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that:
(i) ABCD is a square
(ii) Diagonal BD bisects ∠B as well as ∠D.
Solution:
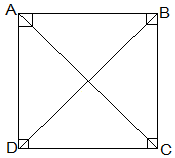
(i) ∠DAC = ∠DCA (AC bisects ∠A as well as ∠C)
⇒ AD = CD (Sides opposite to equal angles of a triangle are equal)
Also, CD = AB (Opposite sides of a rectangle), AB = BC = CD = AD
Thus, ABCD is a square.
(ii) In ΔBCD,
BC = CD
⇒ ∠CDB = ∠CBD (Angles opposite to equal sides are equal)
Also, ∠CDB = ∠ABD (Alternate interior angles)
⇒ ∠CBD = ∠ABD
Thus, BD bisects ∠B
Now,
∠CBD = ∠ADB
⇒ ∠CDB = ∠ADB
Thus, BD bisects ∠B as well as ∠D.
9. In parallelogram ABCD, two points, P and Q, are taken on diagonal BD such that DP = BQ (see Fig. 8.20). Show that:
(i) ΔAPD ≅ ΔCQB
(ii) AP = CQ
(iii) ΔAQB ≅ ΔCPD
(iv) AQ = CP
(v) APCQ is a parallelogram
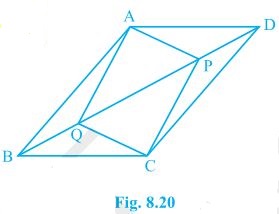
Solution:
(i) In ΔAPD and ΔCQB,
DP = BQ (Given)
∠ADP = ∠CBQ (Alternate interior angles)
AD = BC (Opposite sides of a parallelogram)
Thus, ΔAPD ≅ ΔCQB [SAS congruency]
(ii) AP = CQ by CPCT as ΔAPD ≅ ΔCQB.
(iii) In ΔAQB and ΔCPD,
BQ = DP (Given)
∠ABQ = ∠CDP (Alternate interior angles)
AB = CD (Opposite sides of a parallelogram)
Thus, ΔAQB ≅ ΔCPD [SAS congruency]
(iv) As ΔAQB ≅ ΔCPD
AQ = CP [CPCT]
(v) From questions (ii) and (iv), it is clear that APCQ has equal opposite sides and also has equal and opposite angles. Hence, APCQ is a parallelogram.
10. ABCD is a parallelogram, and AP and CQ are perpendiculars from vertices A and C on diagonal BD (see Fig. 8.21). Show that:
(i) ΔAPB ≅ ΔCQD
(ii) AP = CQ
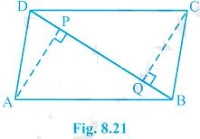
Solution:
(i) In ΔAPB and ΔCQD,
∠ABP = ∠CDQ (Alternate interior angles)
∠APB = ∠CQD (= 90o as AP and CQ are perpendiculars)
AB = CD (ABCD is a parallelogram), ΔAPB ≅ ΔCQD [AAS congruency]
(ii) As ΔAPB ≅ ΔCQD, AP = CQ [CPCT]
11. In ΔABC and ΔDEF, AB = DE, AB || DE, BC = EF and BC || EF. Vertices A, B and C are joined to vertices D, E and F, respectively (see Fig. 8.22).
Show that:
(i) quadrilateral ABED is a parallelogram
(ii) quadrilateral BEFC is a parallelogram
(iii) AD || CF and AD = CF
(iv) quadrilateral ACFD is a parallelogram
(v) AC = DF
(vi) ΔABC ≅ ΔDEF.
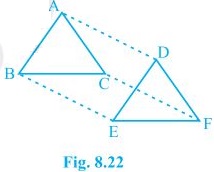
Solution:
(i) AB = DE and AB || DE (Given)
Two opposite sides of a quadrilateral are equal and parallel to each other.
Thus, quadrilateral ABED is a parallelogram
(ii) Again BC = EF and BC || EF.
Thus, quadrilateral BEFC is a parallelogram.
(iii) Since ABED and BEFC are parallelograms.
⇒ AD = BE and BE = CF (Opposite sides of a parallelogram are equal), AD = CF.
Also, AD || BE and BE || CF (Opposite sides of a parallelogram are parallel), AD || CF
(iv) AD and CF are opposite sides of quadrilateral ACFD which are equal and parallel to each other. Thus, it is a parallelogram.
(v) Since ACFD is a parallelogram
AC || DF and AC = DF
(vi) In ΔABC and ΔDEF,
AB = DE (Given)
BC = EF (Given)
AC = DF (Opposite sides of a parallelogram), ΔABC ≅ ΔDEF [SSS congruency]
12. ABCD is a trapezium in which AB || CD and AD = BC (see Fig. 8.23). Show that:
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ΔABC ≅ ΔBAD
(iv) diagonal AC = diagonal BD
[Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.]
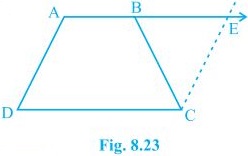
Solution:
To Construct: Draw a line through C parallel to DA intersecting AB produced at E.
(i) CE = AD (Opposite sides of a parallelogram)
AD = BC (Given), BC = CE
⇒∠CBE = ∠CEB
also,
∠A+∠CBE = 180° (Angles on the same side of transversal and ∠CBE = ∠CEB)
∠B +∠CBE = 180° ( As Linear pair)
⇒∠A = ∠B
(ii) ∠A+∠D = ∠B+∠C = 180° (Angles on the same side of transversal)
⇒∠A+∠D = ∠A+∠C (∠A = ∠B)
⇒∠D = ∠C
(iii) In ΔABC and ΔBAD,
AB = AB (Common)
∠DBA = ∠CBA
AD = BC (Given), ΔABC ≅ ΔBAD [SAS congruency]
(iv) Diagonal AC = diagonal BD by CPCT as ΔABC ≅ ΔBAD.
A figure formed by joining four points in an order is called a quadrilateral. This exercise questions are based on the different types of quadrilaterals, their properties and especially those of parallelograms. This exercise of NCERT Class 9 Maths Solutions is based on some very special properties of quadrilateral, such as:
- A diagonal of a parallelogram divides it into two congruent triangles.
- In a parallelogram, opposite sides are equal, and opposite angles are equal.
- If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
- If in a quadrilateral, each pair of opposite angles is equal, then it is a parallelogram.
- If the diagonals of a quadrilateral bisect each other, then it is a parallelogram.
- A quadrilateral is a parallelogram if a pair of opposite sides are equal and parallel.















THANKS A LOT, IT WAS REALLY HELPFUL.
It was very really helpful for me
Nice content, I like it