An LCR circuit is also a resonant or tuned circuit. It consists of an inductor-L, capacitor-C, and resistor-R connected in either series or parallel.

In this article, we will learn about an electrical circuit where an AC voltage is applied across an inductor, a capacitor, and a resistor connected in series.

Table of Content

• Derivation of AC Voltage Applied to Series LCR Circuit
• Frequently Asked Questions-FAQs

Derivation of AC Voltage Applied to Series LCR Circuit

Consider the circuit shown above. Here, we have an inductor, a resistor, and a capacitor connected through a series connection across an AC voltage source given by V. Here, the voltage is sinusoidal in nature and is given by the equation,

Here, v_m is the amplitude of the voltage, and ω is the frequency.

If q is the charge on the capacitor and i the current at time t, we have, from Kirchhoff’s loop rule:

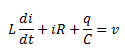
Here, q is the charge held by the capacitor, I is the current passing through the circuit, R is the resistance of the resistor and C is the capacitance of the capacitor. To determine the instantaneous current or the phase of the relationship, we will follow the analytical analysis of the circuit.

Analytical solution

As i

, we can write

Hence, by writing the voltage equation in terms of the charge q through the circuit, we can write,

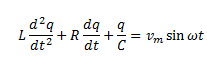
The above equation can be considered analogous to the equation of a forced, damped oscillator. To solve the equation, we assume a solution given by,

So,

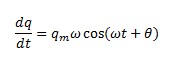
And

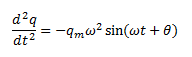
Substituting these values in the voltage equation, we can write,

Here, we have substituted the value of X_c and X_L by Xc = 1/ωC and XL = ω L.

As we know,

hence, substituting this value in the above equation, we get,

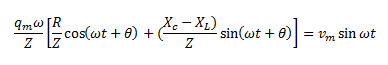
Now, let

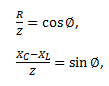
So we can say,

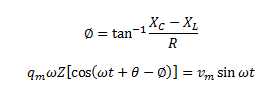
Now, comparing the two sides of the equation, we can write,

And,

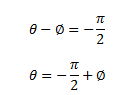
Hence, the equation for current in the circuit can be given as,

Also read:
Impedance of an LCR Circuit

To learn more about the analytical solution for AC voltage and current through a circuit with AC voltage applied across a combination of resistor, inductor and capacitor and other related topics, download BYJU’S – The Learning App.

The video examines the questions asked on the topic of alternating current by analyzing previous year’s JEE Mains & Advanced papers.