In this article, we will be learning about the angular momentum of electrons in detail. We will also be learning about De Broglie’s Explanation of the Quantization of Angular Momentum of Electrons.
| Table of Contents |
What is Angular Momentum of Electron?
Bohr’s atomic model laid down various postulates for the arrangement of electrons in different orbits around the nucleus. According to Bohr’s atomic model, the angular momentum of electrons orbiting around the nucleus is quantized. He further added that electrons move only in those orbits where the angular momentum of an electron is an integral multiple of h/2. This postulate regarding the quantisation of angular momentum of an electron was later explained by Louis de Broglie. According to him, a moving electron in its circular orbit behaves like a particle-wave.
The angular momentum of an electron by Bohr is given by mvr or nh/2π (where v is the velocity, n is the orbit in which the electron is revolving, m is mass of the electron, and r is the radius of the nth orbit).
Among the various proposed models over the years, the Quantum Mechanical Model seems to best fit all properties. Watch the video to learn more about the features of the quantum mechanical model.
De Broglie’s Explanation to the Quantization of Anfgular Momentum of Electron:
The behaviour of particle waves can be viewed analogously to the waves travelling on a string. Particle waves can lead to standing waves held under resonant conditions. When a stationary string is plucked, a number of wavelengths are excited. On the other hand, we know that only those wavelengths survive which form a standing wave in the string, that is, which have nodes at the ends.
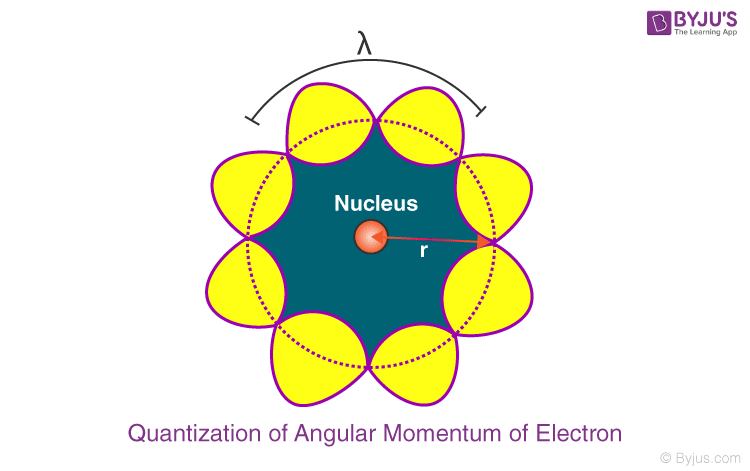
Thus, in a string, standing waves are formed only when the total distance travelled by a wave is an integral number of wavelengths. Hence, for any electron moving in kth circular orbit of radius rk, the total distance is equal to the circumference of the orbit, 2πrk.
Let this be equation (1).
Where,
λ is the de Broglie wavelength.
We know that de Broglie wavelength is given by:
Where,
p is electron’s momentum
h = Planck’s constant
Hence,
Let this be equation (2).
Where mvk is the momentum of an electron revolving in the kth orbit. Inserting the value of λ from equation (2) in equation (1) we get,
mvkrk = kh/2π |
Hence, de Broglie hypothesis successfully proves Bohr’s second postulate stating the quantization of angular momentum of the orbiting electron. We can also conclude that the quantized electron orbits and energy states are due to the wave nature of the electron.
|
Related Articles |
Frequently Asked Questions – FAQs
Is it possible for electrons to have angular momentum?
How to find the angular momentum of an electron?
Is the Angular momentum of an electron quantised?
What is Bohr’s atomic model?
Who proposed the quantization of angular momentum?
To learn more physics concepts with the help of interactive and engaging video lessons, download BYJU’S – The Learning App.
Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz
Visit BYJU’S for all Physics related queries and study materials
Your result is as below
Comments