What Is Simple Harmonic Motion?
A Simple Harmonic Motion, or SHM, is defined as a motion in which the restoring force is directly proportional to the displacement of the body from its mean position. The direction of this restoring force is always towards the mean position. The acceleration of a particle executing simple harmonic motion is given by a(t) = -ω2 x(t). Here, ω is the angular velocity of the particle.
Download Complete Chapter Notes of Simple Harmonic Motion
Download Now
Table of Contents
- Difference between Simple Harmonic, Periodic and Oscillation Motion
- Types of Simple Harmonic Motion
- General Terms
- Differential Equation
- Angular SHM
- Quantitative Analysis
- Necessary Conditions
- Energy in SHM
- Geometrical Interpretations
- Horizontal Phasor
Simple Harmonic, Periodic and Oscillation Motion
Simple harmonic motion can be described as an oscillatory motion in which the acceleration of the particle at any position is directly proportional to the displacement from the mean position. It is a special case of oscillatory motion.
All the Simple Harmonic Motions are oscillatory and also periodic, but not all oscillatory motions are SHM. Oscillatory motion is also called the harmonic motion of all the oscillatory motions, wherein the most important one is Simple Harmonic Motion (SHM).
In this type of oscillatory motion, displacement, velocity and acceleration, and force vary (w.r.t time) in a way that can be described by either sine (or) the cosine functions collectively called sinusoids.
Also Read:
The study of Simple Harmonic Motion is very useful and forms an important tool in understanding the characteristics of sound waves, light waves and alternating currents. Any oscillatory motion which is not simple harmonic can be expressed as a superposition of several harmonic motions of different frequencies.
Difference between Periodic, Oscillation and Simple Harmonic Motion
Periodic Motion
- A motion repeats itself after an equal interval of time. For example, uniform circular motion.
- There is no equilibrium position.
- There is no restoring force.
- There is no stable equilibrium position.
Oscillation Motion
- To and fro motion of a particle about a mean position is called an oscillatory motion in which a particle moves on either side of the equilibrium (or) mean position is an oscillatory motion.
- It is a kind of periodic motion bounded between two extreme points. For example, the oscillation of a simple pendulum, spring-mass system.
- The object will keep on moving between two extreme points about a fixed point is called the mean position (or) equilibrium position along any path (the path is not a constraint).
- There will be a restoring force directed towards the equilibrium position (or) mean position.
- In an oscillatory motion, the net force on the particle is zero at the mean position.
- The mean position is a stable equilibrium position.
Simple Harmonic Motion or SHM
- It is a special case of oscillation, along with a straight line between the two extreme points (the path of SHM is a constraint).
- The path of the object needs to be a straight line.
- There will be a restoring force directed towards the equilibrium position (or) mean position.
- The mean position in Simple Harmonic Motion is a stable equilibrium.
Conditions for SHM
Types of Simple Harmonic Motion
The SHM, or Simple Harmonic Motion, can be classified into two types:
- Linear SHM
- Angular SHM
Linear Simple Harmonic Motion
When a particle moves to and fro about a fixed point (called equilibrium position) along with a straight line, then its motion is called linear Simple Harmonic Motion.
For example, the spring-mass system.
Conditions for Linear SHM
The restoring force or acceleration acting on the particle should always be proportional to the displacement of the particle and directed towards the equilibrium position.
- \(\begin{array}{l}\overrightarrow{x}- \text{displacement of particle from equilibrium position}\end{array} \)
- \(\begin{array}{l}\overrightarrow{F}- \text{Restoring force}\end{array} \)
- \(\begin{array}{l}\overrightarrow{a}- \text{acceleration}\end{array} \)
Angular Simple Harmonic Motion
When a system oscillates angular long with respect to a fixed axis, then its motion is called angular simple harmonic motion.
Conditions to Execute Angular SHM
The restoring torque (or) angular acceleration acting on the particle should always be proportional to the angular displacement of the particle and directed towards the equilibrium position.
Τ ∝ θ or α ∝ θ
Where,
- Τ – Torque
- α – Angular acceleration
- θ – Angular displacement
Simple Harmonic Motion Key Terms
Mean Position
The point at which net force acting on the particle is zero.
From the mean position, the force acting on the particle is
Conditions at Mean Position
The force acting on the particle is negative of the displacement. So, this point of equilibrium will be a stable equilibrium.
Amplitude in SHM
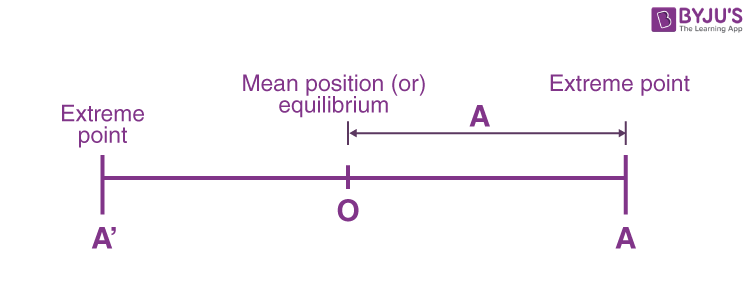
It is the maximum displacement of the particle from the mean position.
Time Period and Frequency of SHM
The minimum time after which the particle keeps on repeating its motion is known as the time period, or the shortest time taken to complete one oscillation is also defined as the time period.
T = 2π/ω
Frequency: The number of oscillations per second is defined as the frequency.
Frequency = 1/T and, angular frequency ω = 2πf = 2π/T
Phase in SHM
The phase of a vibrating particle at any instant is the state of the vibrating or oscillating particle regarding its displacement and direction of vibration at that particular instant.
The expression and position of a particle as a function of time.
x = A sin (ωt + Φ)
Where (ωt + Φ) is the phase of the particle, the phase angle at time t = 0 is known as the initial phase.
Phase Difference
The difference in total phase angles of two particles executing simple harmonic motion with respect to the mean position is known as the phase difference. Two vibrating particles are said to be in the same phase; the phase difference between them is an even multiple of π.
ΔΦ = nπ where n = 0, 1, 2, 3, . . . . .
Two vibrating particles are said to be in opposite phases if the phase difference between them is an odd multiple of π.
ΔΦ = (2n + 1) π where n = 0, 1, 2, 3, . . . . .
Simple Harmonic Motion Equation and Its Solution
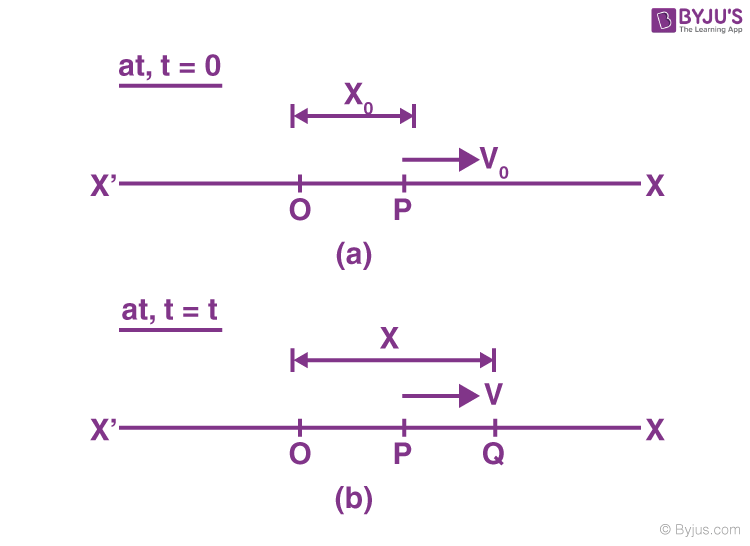
Consider a particle of mass (m) executing Simple Harmonic Motion along a path x o x; the mean position at O. Let the speed of the particle be v0 when it is at position p (at a distance no from O).
At t = 0, the particle at P (moving towards the right)
At t = t, the particle is at Q (at a distance x from O)
With a velocity (v).
K – is a positive constant
Here,
d2x/dt2 + ω2x = 0, which is the differential equation for linear Simple Harmonic Motion.
Solutions of Differential Equations of SHM
The differential equation for the Simple Harmonic Motion has the following solutions:
- \(\begin{array}{l}x=A\sin \omega \,t\end{array} \)(This solution when the particle is in its mean position point (O) in figure (a)
- \(\begin{array}{l}{{x}_{0}}=A\sin \phi\end{array} \)(When the particle is at the position & (not at mean position) in figure (b)
- \(\begin{array}{l}x=A\sin \left( \omega t+\phi \right)\end{array} \)(When the particle at Q at in figure (b) (any time t).
These solutions can be verified by substituting these x values in the above differential equation for the linear simple harmonic motion.
Angular Simple Harmonic Motion
A body free to rotate about an axis can make angular oscillations. For example, a photo frame or a calendar suspended from a nail on the wall. If it is slightly pushed from its mean position and released, it makes angular oscillations.
Conditions for an Angular Oscillation to be Angular SHM
The body must experience a net torque that is restored in nature. If the angle of oscillation is small, this restoring torque will be directly proportional to the angular displacement.
Τ ∝ – θ
Τ = – kθ
Τ = Iα
α = – kθ
This is the differential equation of an angular Simple Harmonic Motion. The solution of this equation is the angular position of the particle with respect to time.
Then the angular velocity,
θ0 – Amplitude of the angular SHM
Example:
- Simple pendulum
- Seconds pendulum
- The physical pendulum
- Torsional pendulum
Quantitative Analysis of SHM
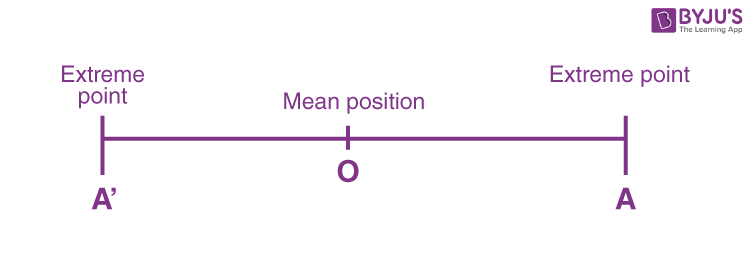
Let us consider a particle executing Simple Harmonic Motion between A and A1 about passing through the mean position (or) equilibrium position (O). Its analysis is as follows
SHM about Position O
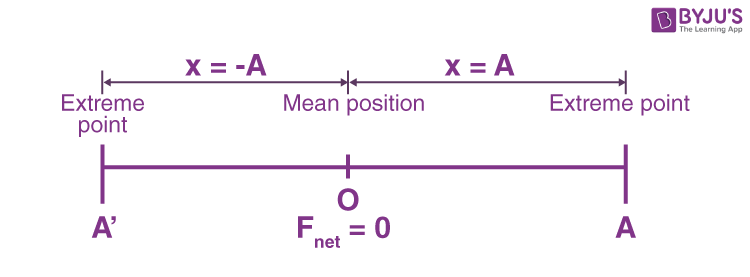
| Displacement | x = -A | x = 0 | x = +A |
| Acceleration | |a| = Max | a = 0 | |a| = max |
| Speed | |v| = 0 | |v| = Max | |v| = 0 |
| Kinetic energy | KE = 0 | KE = Max | KE = 0 |
| Potential energy | PE = Max | PE = Min | PE = Max |
Equation of Position of a Particle as a Function of Time
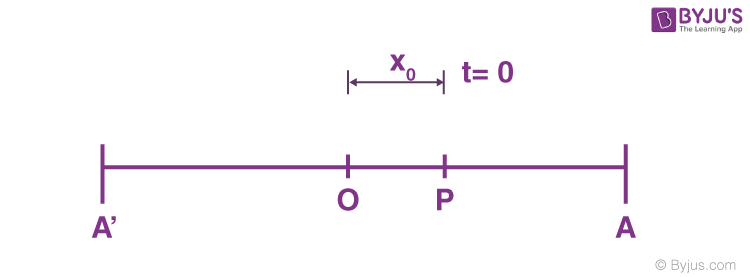
Let us consider a particle, which is executing SHM at time t = 0, and the particle is at a distance from the equilibrium position.
Necessary Conditions for Simple Harmonic Motion
- \(\begin{array}{l}\overrightarrow{F}\propto -\overrightarrow{x}\end{array} \)
- \(\begin{array}{l}\overrightarrow{a}\propto -\overrightarrow{x}\end{array} \)
- \(\begin{array}{l}\overrightarrow{a}=-{{\omega }^{2}}x\end{array} \)
- \(\begin{array}{l}\overrightarrow{a}=\frac{dv}{dx}\frac{dx}{dt}=v\frac{dv}{dx}\end{array} \)
- \(\begin{array}{l}\overrightarrow{a}=v\frac{dv}{dx}=-{{\omega }^{2}}x\end{array} \)
- \(\begin{array}{l}\int\limits_{0}^{v}{vdv}=\int\limits_{0}^{x}{-{{\omega }^{2}}xdx}\end{array} \)
- \(\begin{array}{l}\frac{{{v}^{2}}}{2}=\frac{-{{\omega }^{2}}{{x}^{2}}}{2}+c….(1)\end{array} \)
Some conditions we know:
At point A v = 0 [x = A] the equation (1) becomes
Sub the value of C in equation (1)
Where v is the velocity of the particle executing simple harmonic motion from the definition of instantaneous velocity
x = Asin ( ωt + Φ) . . . . . (3)
Equation (3) – Equation of the position of a particle as a function of time.
Case 1: If at t = 0
The particle at x = x0
Φ is the initial phase of the particle.
Case 2: If at t = 0
The particle at x = 0
i.e. Φ = 0
Case 3: If the particle is at one of its extreme positions, x = A at t = 0
⇒ π/2 = Φ
So, the value can be anything depending upon the position of the particle at t = 0. That is why it is called the initial phase of the particle.
Now, if we see the equation of the position of the particle with respect to time,
π/2 = x = A sin ( ωt + Φ)
sin (ωt + Φ) is the periodic function, whose period is T = 2π/ω
Which can be anything, sine function or cosine function
Time Period of SHM
The coefficient of t is ω.
So, the time period T = 2π/ω
ω =2π/T = 2πf
ωt = Angular frequency of SHM
From the expression of particle position as a function of time:
The Velocity of a Particle Executing Simple Harmonic Motion
Velocity in SHM is given by v = dx/dt,
x = A sin (ωt + Φ)
Since x = A sin ωt
On squaring both sides,
The curve between displacement and velocity of a particle executing the simple harmonic motion is an ellipse.
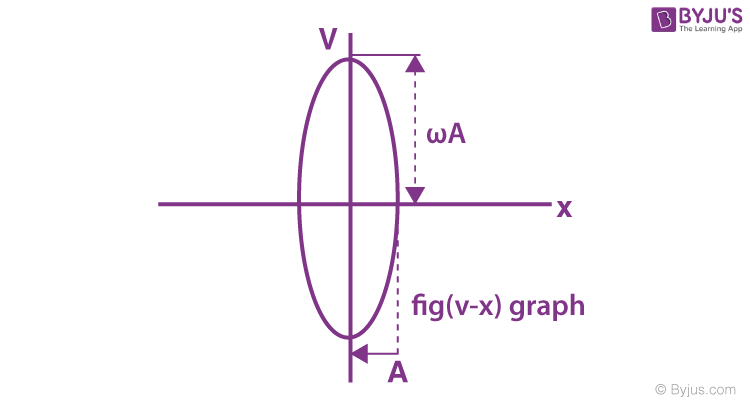
When ω = 1, then the curve between v and x will be circular.
Acceleration in SHM
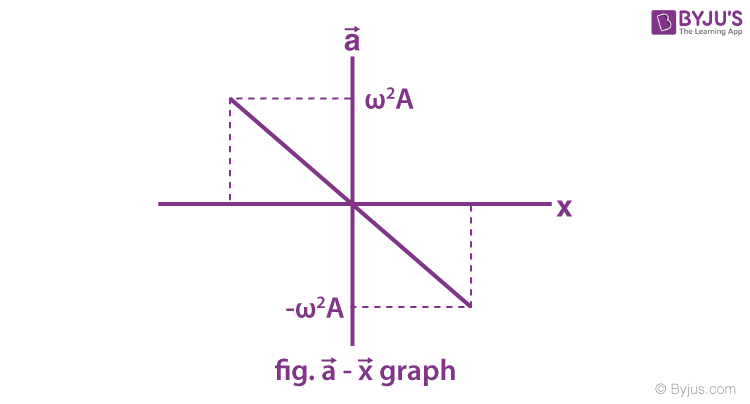
Hence, the expression for displacement, velocity and acceleration in linear simple harmonic motion is
- x = A sin ( ωt + Φ)
- \(\begin{array}{l}v = A\omega \cos \left( \omega t+\phi \right)=\omega \sqrt{{{A}^{2}}-{{x}^{2}}}\end{array} \)and
- \(\begin{array}{l}a = -A{{\omega }^{2}}\sin \left( \omega t+\phi \right)=-{{\omega }^{2}}x\end{array} \)
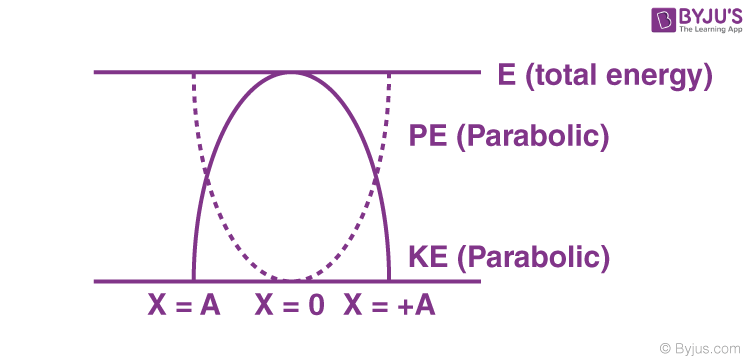
Energy in Simple Harmonic Motion (SHM)
The system that executes SHM is called the harmonic oscillator.
Consider a particle of mass m, executing linear simple harmonic motion of angular frequency (ω) and amplitude (A),
x = A sin (ωt + Φ)
F = -kx, where k = mω2.
Kinetic Energy of a Particle in SHM
Kinetic Energy
Therefore, the Kinetic Energy
Potential Energy of SHM
The total work done by the restoring force in displacing the particle from (x = 0) (mean position) to x = x:
When the particle has been displaced from x to x + dx, the work done by restoring force is
dw = F dx = -kx dx
Potential Energy = -(work done by restoring force)
Total Mechanical Energy of the Particle Executing SHM
E = KE + PE
Hence, the particle’s total energy in SHM is constant, independent of the instantaneous displacement.
⇒ Relationship between kinetic energy, potential energy and time in Simple Harmonic Motion at t = 0, when x = ±A.
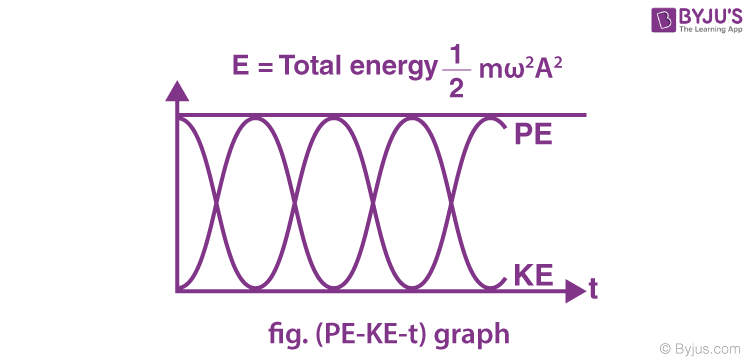
⇒ Variation of kinetic energy and potential energy in Simple Harmonic Motion with displacement.
Geometrical Interpretation of Simple Harmonic Motion
If a particle is moving with uniform speed along the circumference of a circle, then the straight line motion of the foot of the perpendicular drawn from the particle on the diameter of the circle is called simple harmonic motion.
SHM as a Projection of Circular Motion
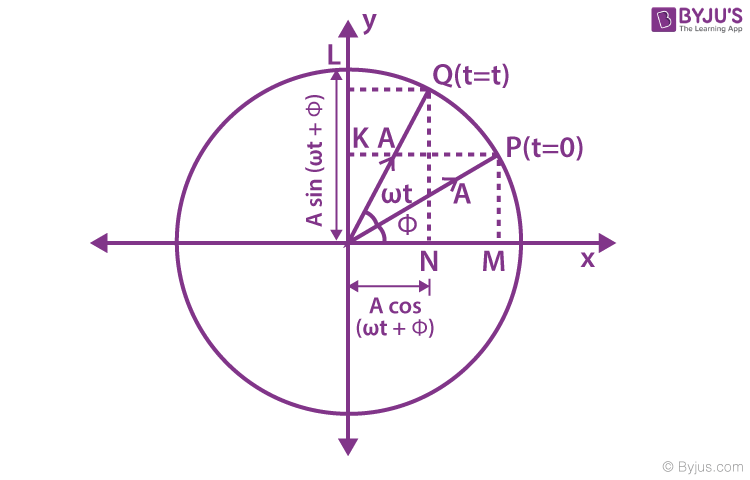
The particle is at position P at t = 0 and revolves along a circle with a constant angular velocity (ω). The projection of P on the diameter along the x-axis (M). At the later time (t), the particle is at Q. Now, its projection on the diameter along the x-axis is N.
As the particle P revolves around in a circle anti-clockwise, its projection M follows it up, moving back and forth along the diameter, such that the displacement of the point of projection at any time (t) is the x-component of the radius vector (A).
x = A cos ( ωt + Φ) . . . . . . . (1)
y = A sin ( ωt + Φ) . . . . . (2)
Thus, we see that the uniform circular motion is the combination of two mutually perpendicular linear harmonic oscillations.
It implies that P is under uniform circular motion, (M and N) and (K and L) are performing simple harmonic motion about O with the same angular speed ω as that of P.
P is under uniform circular motion, which will have centripetal acceleration along A (radius vector).
It can be resolved into two components:
- \(\begin{array}{l}{{a}_{N}}=A{{\omega }^{2}}{{\sin }^{2}}\left( \omega t+\phi \right)\end{array} \)
- \(\begin{array}{l}{{a}_{L}}=A{{\omega }^{2}}{{\cos }^{2}}\left( \omega t+\phi \right)\end{array} \)
aN and aL acceleration correspond to the points N and L, respectively.
In the above discussion, the foot of the projection on the x-axis is called a horizontal phasor.
Similarly, the foot of the perpendicular on the y-axis is called the vertical phasor. We already know the vertical and horizontal phasor will execute the simple harmonic motion of amplitude A and angular frequency ω. The phases of the two SHMs differ by π/2.
Video Lessons
Simple Harmonic Motion Short Notes

Simple Harmonic Motion (SHM) – JEE Concept

Angular SHM (Simple Harmonic Motion)

What Is Energy in SHM?

Graphical Representation of SHM

Simple Harmonic Motion – Top 12 Most Important and Expected JEE Questions

Waves and Simple Harmonic Motion Important Questions

Problem-solving Strategy in Horizontal Phasor
- Let us assume a circle of radius equal to the amplitude of SHM.
- Assume a particle rotating in a circular path moving with constant same as that of simple harmonic motion in the clockwise direction.
- The angle made by the particle at t = 0 with the upper vertical axis is equal to φ (phase constant).
- The horizontal component of the velocity of a particle gives you the velocity of a particle performing the simple harmonic motion.
- The component of the acceleration of a particle in the horizontal direction is equal to the acceleration of the particle performing SHM. [In uniform circular acceleration centripetal only ac = ω2A].
Frequently Asked Questions on Simple Harmonic Motion
What is a simple harmonic motion?
Simple harmonic motion is a periodic motion in which the particle acceleration is directly proportional to its displacement and is directed towards the mean position.
What is the formula for restoring force in SHM?
The restoring force is given by the formula
F = -kx
The negative sign shows that the force is in the opposite direction.
k is the force constant.
x is the displacement of the string from the equilibrium position.
Mention the difference between harmonic motion and simple harmonic motion.
The harmonic motion is when the restoring force is proportional to the displacement but in opposite directions. Simple Harmonic Motion is a harmonic motion with a constant amplitude and the same frequency.
What is damped simple harmonic motion?
The periodic motion of gradually decreasing amplitude is called the damped simple harmonic motion.
What is the displacement of the particle executing simple harmonic motion?
Distance travelled by the particle from its mean position at any instant is called the displacement of the particle executing simple harmonic motion.
At what points is the energy entirely kinetic and entirely potential in simple harmonic motion?
At the mean position, the energy is entirely kinetic energy. At the extreme position, the energy is entirely potential energy.
What is the phase difference between displacement and acceleration of the particle executing simple harmonic motion?
The phase difference between displacement and acceleration of the particle executing simple harmonic motion is π radian.
What is meant by the amplitude of simple harmonic motion?
The maximum displacement of the particle is called the amplitude of motion.

Comments