The branch of physics that defines motion with respect to space and time, ignoring the cause of that motion, is known as kinematics. Kinematics equations are a set of equations that can derive an unknown aspect of a body’s motion if the other aspects are provided.
These equations link five kinematic variables:
- Displacement (denoted by Δx)
- Initial Velocity v0
- Final Velocity denoted by v
- Time interval (denoted by t)
- Constant acceleration (denoted by a)
Essentially, kinematics equations can derive one or more of these variables if the others are given. These equations define motion at either constant velocity or at constant acceleration. Because kinematics equations are only applicable at a constant acceleration or a constant speed, we cannot use them if either of the two is changing.
Inverse Kinematics:
Inverse Kinematics does the reverse of kinematics and in case we have the endpoint of a particular structure, certain angle values would be needed by the joints to achieve that endpoint. It is a little difficult and has generally more than one or even infinite solutions.
There are four basic kinematics equations:
- \(\begin{array}{l}v=v_{0}+at\end{array} \)
- \(\begin{array}{l}\Delta x=(\frac{v+v_{0}}{2})t\end{array} \)
- \(\begin{array}{l}\Delta x= v_{0}t+\frac{1}{2}at^{2}\end{array} \)
- \(\begin{array}{l}v^{^{2}}=v_{o}^{2}+2a\Delta x\end{array} \)
It can be noticed that if any four of the variables are given, we can easily calculate the fifth variable using kinematic equations.
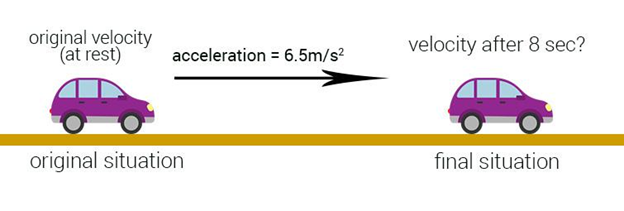
For example, if it is given that a car is travelling and it accelerates from its resting position with an acceleration of 6.5 m/s2 for a time span of 8 seconds, reaching a final velocity of 42 m/s, east and a displacement of 120 m, then the motion of this car is fully described. Now, if anyone of this information was not provided, we could have easily calculated it with the help of kinematics equations.
Rotational Kinematics Equations
Till now, we were looking at the Translational or linear kinematics equation which deals with the motion of a linearly moving body. There is another branch of kinematics equations which deals with the rotational motion of anybody. These are, however, just a corollary of the previous equations with just the variables changed.
- Displacement is replaced by a change in angle.
- Initial and final velocities are replaced by initial and final angular velocity.
- Acceleration is replaced by angular acceleration
- Time is the only constant.
| Rotational Motion (α = constant) | Linear Motion (a = constant) |
\(\begin{array}{l}\omega =\omega_{0}+\alpha t\end{array} \) |
\(\begin{array}{l}v=v_{0}+at\end{array} \) |
\(\begin{array}{l}\Theta =\frac{1}{2}(\omega+\omega_{0})t\end{array} \) |
\(\begin{array}{l}x=\frac{1}{2}(v_{0}+v)t\end{array} \) |
\(\begin{array}{l}\Theta =\omega_{0}t+\frac{1}{2}\alpha t^{2}\end{array} \) |
\(\begin{array}{l}x=v_{0}t+\frac{1}{2}at^{2}\end{array} \) |
\(\begin{array}{l}\omega^{2} =\omega_{0}^{2}+2\alpha \Theta\end{array} \) |
\(\begin{array}{l}v^{2}=v_{0}^{2}+2ax\end{array} \) |
Stay tuned to BYJU’S to know more about kinetic energy, kinematics, and much more.
Watch the video below to understand more about motion in BYJU’S way.
Frequently Asked Questions – FAQs
What is centripetal acceleration?
What is kinematics?
What is radial acceleration?.
Define kinetic energy.
When is the kinetic energy maximum?
Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz
Visit BYJU’S for all Physics related queries and study materials
Your result is as below
It’s nice tqqq