Standard deviation formula is used to find the values of a particular data that is dispersed. In simple words, the standard deviation is defined as the deviation of the values or data from an average mean. Lower standard deviation concludes that the values are very close to their average. Whereas higher values mean the values are far from the mean value. It should be noted that the standard deviation value can never be negative.
Standard Deviation is of two types:
- Population Standard Deviation
- Sample Standard Deviation
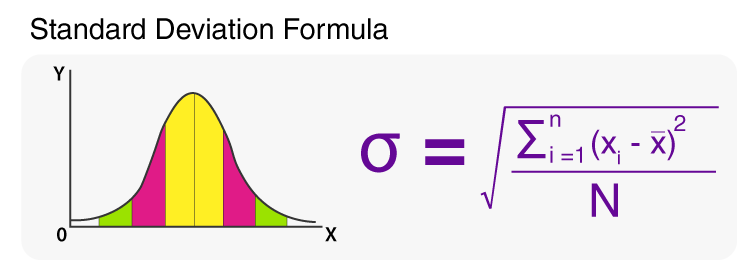
Formula to Calculate Standard Deviation
Formulas for Standard Deviation
| Population Standard Deviation Formula | \(\begin{array}{l}\sigma=\sqrt{\frac{\sum(X-\mu)^{2}}{n}}\end{array} \) |
| Sample Standard Deviation Formula | \(\begin{array}{l}s=\sqrt{\frac{\sum(X-\bar{X})^{2}}{n-1}}\end{array} \) |
Notations for Standard Deviation
- σ = Standard Deviation
- xi = Terms Given in the Data
- x̄ = Mean
- n = Total number of Terms
Standard Deviation Formula Based on Discrete Frequency Distribution
For discrete frequency distribution of the type:
x: x1, x2, x3, … xn and
f: f1, f2, f3, … fn
The formula for standard deviation becomes:
Here, N is given as:
N = n∑i=1 fi
Standard Deviation Formula for Grouped Data
There is another standard deviation formula which is derived from the variance. This formula is given as:
Also Check: Difference Between Variance and Standard Deviation
Example Question based on Standard Deviation Formula
Question: During a survey, 6 students were asked how many hours per day they study on an average? Their answers were as follows: 2, 6, 5, 3, 2, 3. Evaluate the standard deviation.
Solution:
Find the mean of the data:
Step 2: Construct the table:
| x1 | x1 − x̄ | (x1 − x̄)2 |
| 2 | -1.5 | 2.25 |
| 6 | 2.5 | 6.25 |
| 5 | 1.5 | 2.25 |
| 3 | -0.5 | 0.25 |
| 2 | -1.5 | 2.25 |
| 3 | -0.5 | 0.25 |
| = 13.5 |
Step 3: Now, use the Standard Deviation formula
Sample Standard Deviation =
=√(13.5/[6-1])
=√[2.7]
=1.643
To check more maths formulas for different classes and for various concepts, stay tuned with BYJU’S. Also, register now to get access to various video lessons and get a more effective and engaging learning experience.
Comments