Surface Area of a Prism Formula
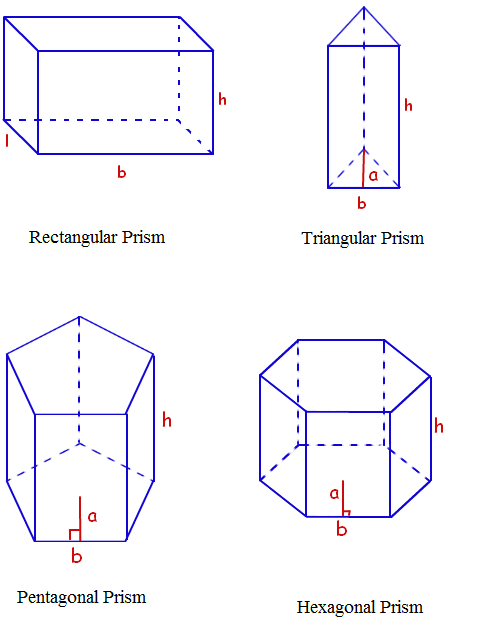
A prism is a polyhedron with 2 polygonal bases parallel to each other. The two polygonal bases are joined by lateral faces. The number of lateral faces are equal to the number of sides in the base. The lateral faces in a prism are perpendicular to the polygonal bases. Surface area of a prism is the sum of the area of the 2 polygonal bases and the area of the lateral faces. The surface area of a prism is measured in terms of square units.

The Surface Area of a Prism Formula is given as,
Surface Area Of A Rectangular Prism is A = 2 (wl + lh + hw)
Surface Area Of A Triangular Prism is A = bh + L (s1 + s2 + s3)


Where,
a – apothem length of the prism.
b – base length of the prism.
l – base width of the rectangular prism.
h – height of the prism.
Surface Area of a Prism Problems
Some solved problems on the surface area of a prism are given below :
Solved Examples
Question 1: What will be the surface area of a triangular prism if the apothem length, base length and height are 7 cm, 10 cm and 18 cm respectively ?
Solution:
Given,
a = 7 cm
b = 10 cm
h = 18 cm
= 70 cm2 + 540 cm2
= 610 cm2
Solution:
Given,
a = 7 cm
b = 10 cm
h = 18 cm
Surface area of a triangular prism
= ab + 3bh
= (7 cm
\(\begin{array}{l}\times\end{array} \)
10 cm) + (3 \(\begin{array}{l}\times\end{array} \)
10 cm \(\begin{array}{l}\times\end{array} \)
18 cm)= 70 cm2 + 540 cm2
= 610 cm2
Question 2: Calculate the surface area of a pentagonal prism with apothem length, base length and height as 12 cm, 15 cm, and 21 cm respectively ?
Solution:
Given,
a = 12 cm
b = 15 cm
h = 21 cm
= 900 cm2 + 1575 cm2
= 2475 cm2
Solution:
Given,
a = 12 cm
b = 15 cm
h = 21 cm
Surface area of a pentagonal prism
= 5ab + 5bh
= (5
\(\begin{array}{l}\times\end{array} \)
12 cm \(\begin{array}{l}\times\end{array} \)
15 cm) + (5 \(\begin{array}{l}\times\end{array} \)
15 cm \(\begin{array}{l}\times\end{array} \)
21 cm)= 900 cm2 + 1575 cm2
= 2475 cm2
| More topics in Surface Area of a Prism Formula | |
| Surface Area of a Triangular Prism Formula | Surface Area of a Rectangular Prism Formula |
Comments